Introduction 1. 1-Minute Summary 2. X-Ray Vision 3. 3d Intuition 4. Integrals, Derivatives 5. Computer Notation 6. Improved Algebra 7. Linear Changes 8. Squared Changes 9. Infinity 10. Derivatives 11. Fundamental Theorem 12. Add, Multiply, Invert 13. Patterns In The Rules 14. Take Powers, Divide 15. Archimedes' Formulas Summary

1. Intuition-First Learning

Concept	Key Analogy / Takeaway
Learning Strategy: Blurry, then refine
Music Analogy	In music: Appreciation (sounds good!), description (hum it), symbols (sheet music), performance (play it) In math: Appreciation (aha!), description (English), symbols (math), performance (calculate)
Appreciation vs. Performance	We can enjoy listening to music even if we can't play it. We can think with calculus even if we can't (yet) compute with calculus.

2. Appreciating Calculus

Concept	Key Analogy / Takeaway
Calculus in 1 minute	See the world with X-Ray and Time-Lapse vision.
Calculus in 10 minutes	New viewpoints lead to insights: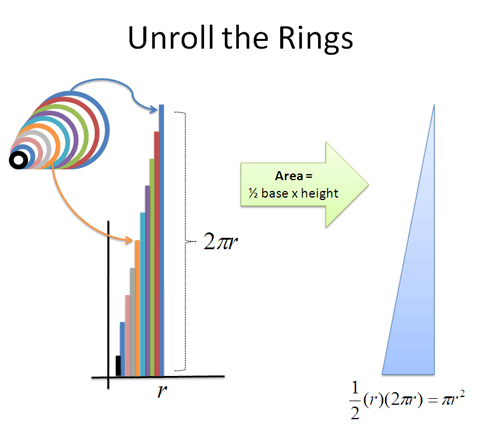 Calculus explains X-Ray and Time-Lapse vision exist, they are opposites (splitting apart, gluing together) and any pattern can be analyzed. Arithmetic gives us add/subtract, multiply/divide, exponents/roots. "Calculus arithmetic" also has X-Ray (split apart) and Time-Lapse (glue together).
So what can I do with Calculus?	See patterns at a deeper level and make predictions we couldn't before.
Example: Analyzing a Circle	Build with rings, slices, or boards; each has tradeoffs.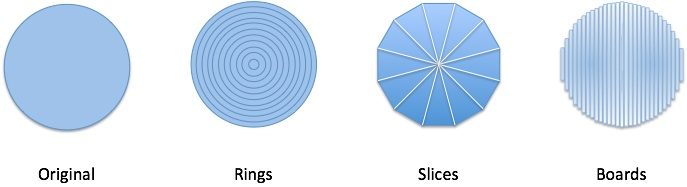
Ring-by-ring View	Organic growth, increasing effort.
Slice-by-slice View	Assembly-line, predictable progress
Board-by-board View	Robotic, never retracing
3d versions
How to think with calculus	For your situation: X-Ray: What's the next thing that will happen? Any trend? Time-lapse: What outcome are these changes leading to?

3. Describing Calculus (English → Math)

Concept	Key Analogy / Takeaway
Organize Our Descriptions	Direction of slices in orange. Arrange slices side-by-side for easy comparison.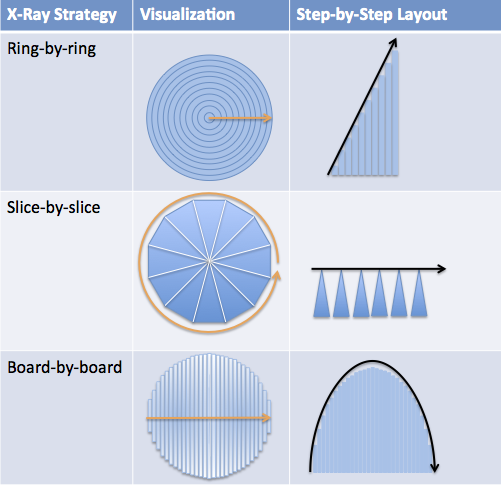
Term: Derivative	Creating a pattern of step-by-step slices along a path (i.e., rings, slices, boards, etc.).
Term: Integral	Accumulating slices into a shape (what is being built up as we go?)
Notation Details	Derivatives only require the direction we move when taking slices: $$$\frac{d}{dr}$$$ means slice along r's direction. Integrals require direction we glue together ($$$dr$$$), where we start/stop ($$$0$$$ to $$$r$$$), and the size of each slice ($$$2 \pi r \ dr$$$: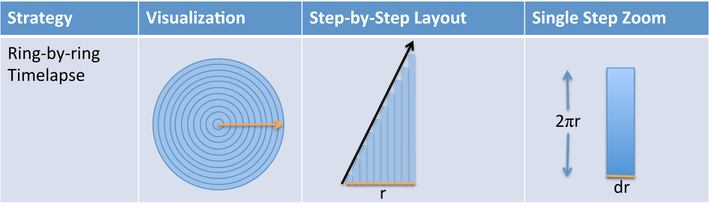
Computer Calculation	Wolfram Alpha can compute integrals/derivatives when asked: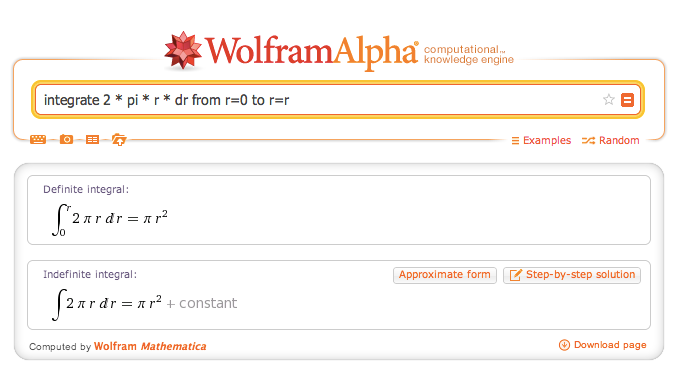
Note about Abstraction	Begin thinking about general patterns (x, x^2), not just specific shapes (a line, a square).
Lines	Lines ($$$f(x) = ax$$$) change by a steady $$$a$$$ each time, like building a fence.
Squares	Squares ($$$f(x) = x^2$$$) change by $$$2x + 1$$$: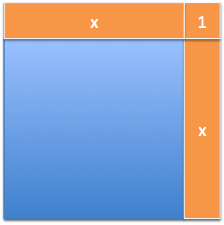

4. Learning To Measure Change

Concept	Key Analogy / Takeaway
Infinite processes can point to a result	Analogy: fly going back and forth. Count its paths ("infinite"), or just the time traveled. Pixellated letters point to the smooth whole.
Analogy: Measuring Heart Rate	Get on treadmill, hook up wires, run. The measurement is your heart rate under stress. Must then remove impact of wires.
The formal derivative	Find change, then assume change had zero effect: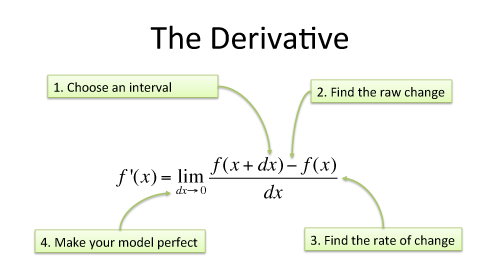
Example	$$$2x + dx \overset{dx \ = \ 0} \Longrightarrow 2x$$$, so $$$\frac{d}{dx} x^2 = 2x$$$, with errors artifacts removed
Fundamental Theorem of Calculus	The shortcut to computing the integral is finding a pattern that made the changes we're seeing.
Integrals are Reverse Engineered	See patterns of steps and ask: what shape could have made this? L-shapes come from changing squares. Instead of adding (5 + 7 + 9 = 21), take the final square and subtract the starting one (25 - 4 = 21).

5. The Core Rules Of Calculus

Concept	Key Analogy / Takeaway
Multiplication Rule $$(f \cdot g)' = f \cdot dg + g \cdot df$$	Grow a garden on two sides; ignore the corner.
Simple Division $$ \left( \frac{1}{x} \right)' = -\frac{1}{x^2}$$	Splitting cake, new person enters (from halves to thirds).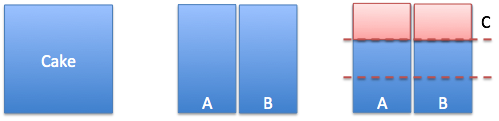
Insight: Each perspective makes a contribution	With 3 variables you have 3 perspectives to add: Derivative of $$$x \cdot x \cdot x$$$ has three identical perspectives ($$$x^2 + x^2 + x^2$$$) or $$$3 x^2$$$.
Power Rule $$\frac{d}{dx} x^n = n x^{n-1} $$	Each side has a point of view; I change, others are the same.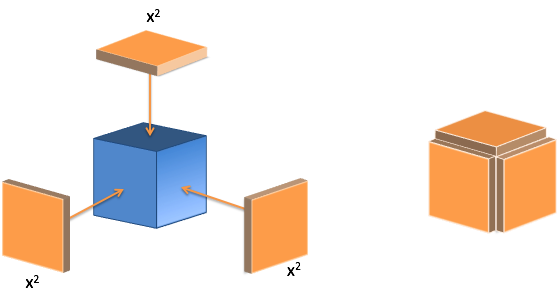
Rule Summary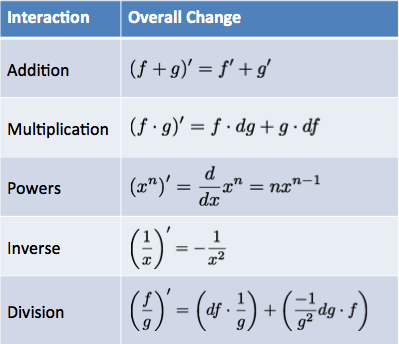

6. Finding Archimedes' Formulas

Concept	Key Analogy / Takeaway
Find the circle/sphere formulas	X-Ray and Time-Lapse a single ring into the other shapes.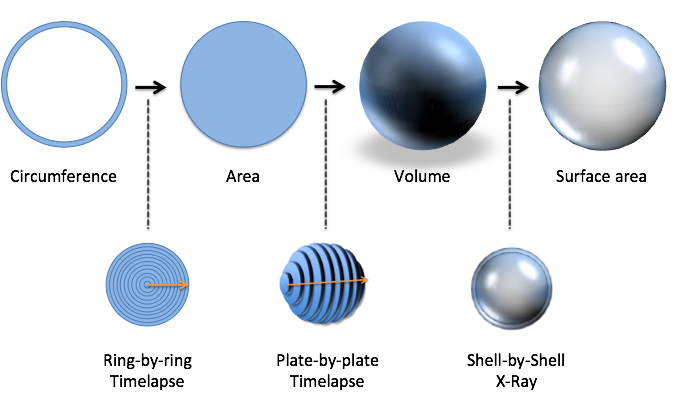
Circumference to Area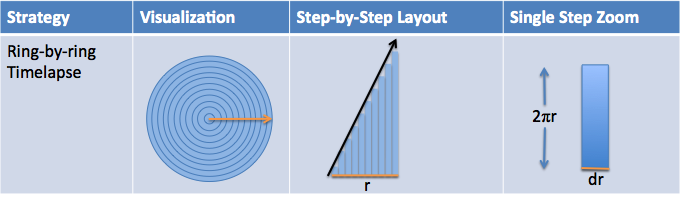
Area to Volume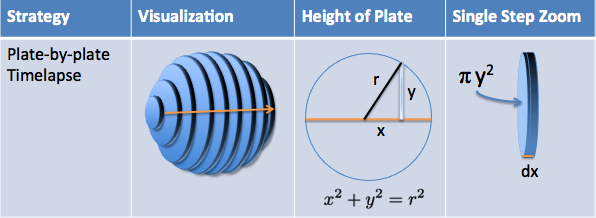
Volume to Surface Area	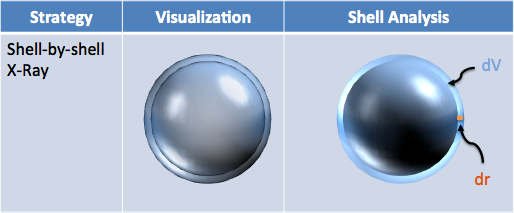$$\text{area of shell} = \frac{\text{volume of shell}}{\text{depth of shell}} = \frac{dV}{dr} $$ $$\frac{d}{dr} V = \frac{d}{dr} \frac{4}{3} \pi r^3 = \frac{4}{3} \pi \frac{d}{dr} r^3 = \frac{4}{3} \pi (3 r^2) = 4 \pi r^2 $$
Historical Note	Archimedes had a calculus mindset: he re-arranged discs, cylinders, cones, etc. to make "easy to measure" slices. The techniques you already know would make him tear up.