10. The Theory Of Derivatives
The last lesson showed that an infinite sequence of steps could lead to a finite conclusion. Let's put it into practice, and see how breaking change into infinitely small parts can point to the the true amount.
Analogy: Measuring Heart Rates
Imagine you're a doctor trying to measure a patient's heart rate while exercising. You put a guy on a treadmill, strap on the electrodes, and get him running. The machine spit out 180 beats per minute. That must be his heart rate, right?
Nope. That's his heart rate when observed by doctors and covered in electrodes. Wouldn't that scenario be stressful? And what if your Nixon-era electrodes get tangled on themselves, and tug on his legs while running?
Ah. We need the electrodes to get some measurement. But, right afterwards, we need to remove the effect of the electrodes themselves. For example, if we measure 180 bpm, and knew the electrodes added 5 bpm of stress, we'd know the true heart rate was 175.
The key is making the knowingly-flawed measurement, to get a reading, then correcting it as if the instrument wasn't there.
Measuring the Derivative
Measuring the derivative is just like putting electrodes on a function and making it run. For $$$f(x) = x^2$$$, we stick an electrode of $$$+1$$$ onto it, to see how it reacted:
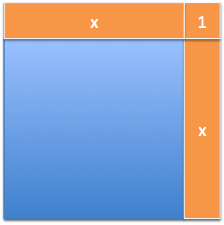
The horizontal stripe is the result of our change applied along the top of the shape. The vertical stripe is our change moving along the side. And what's the corner?
It's part of the horizontal change interacting with the vertical one! This is an electrode getting tangled in its own wires, a measurement artifact that needs to go.
Throwing Away The Artificial Results
The founders of calculus intuitively recognized which components of change were "artificial" and just threw them away. They saw that the corner piece was the result of our test measurement interacting with itself, and shouldn't be included.
In modern times, we created official theories about how this is done:
-
Limits: We let the measurement artifacts get smaller and smaller until they effectively disappear (cannot be distinguished from zero).
-
Infinitesimals: Create a new type of number that lets us try infinitely-small change on a separate, tiny number system. When we bring the result back to our regular number system, the artificial elements are removed.
There are entire classes dedicated to exploring these theories. The practical upshot is realizing how to take a measurement and throw away the parts we don't need.
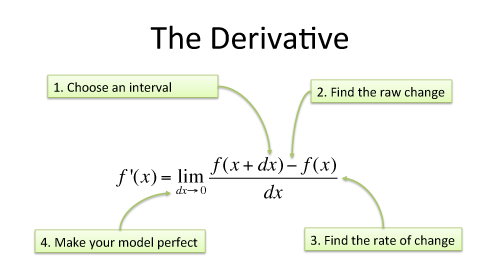
Here's the setup, described with limits:
| Step | Example |
|---|---|
| Prereq: Start with a function to study | $$f(x) = x^2 $$ |
| 1: Change the input by dx, our test change | $$f(x + dx) = (x + dx)^2 = x^2 + 2x\cdot dx + (dx)^2 $$ |
| 2: Find the resulting change in output, $$$df$$$ | $$f(x + dx) - f(x) = 2x\cdot dx + (dx)^2 $$ |
| 3: Find $$$\frac{df}{dx}$$$ | $$\frac{2x\cdot dx + (dx)^2}{dx} = 2x + dx $$ |
| 4: Throw away the measurement artifacts | $$2x + dx \overset{dx \ = \ 0} \Longrightarrow 2x $$ |
Wow! We found the official derivative for $$$\frac{d}{dx} x^2$$$ on our own:
Now, a few questions:
-
Why do we measure $$$\frac{df}{dx}$$$, and not the actual change df? Think of df as the raw change that happened as we made a step. The ratio is helpful because it normalizes comparisons, showing us how much the output reacts to the input. Now, sometimes it can be helpful to isolate the actual change that happened in an interval, and rewrite $$$\frac{df}{dx} = 2x$$$ as $$$df = 2x \cdot dx$$$.
-
How do we set dx to 0? I see dx as the size of the instrument used to measure the change in a function. After we have the measurement with a real instrument ($$$2x + dx$$$), we figure out what the measurement would be if the instrument wasn't there to interfere ($$$2x$$$).
-
But isn't the $$$2x + 1$$$ pattern correct? The integers have the squares 0, 1, 4, 9, 16, 25 which has the difference pattern 1, 3, 5, 7, 9. Because the integers must use a fixed interval of 1, using $$$dx = 1$$$ and keeping it around is a perfectly accurate way to measure how they change. However, decimals don't have a fixed gap, so $$$2x$$$ is the best result for how fast the change between $$$2^2$$$ and $$$(2.0000001)^2$$$ is happening. (Except, replace 2.0000001 with the number immediately following 2.0, whatever that is).
-
If there's no '+1', when does the corner get filled in? The diagram shows how area grows in the presence of a crude instrument, dx. It isn't a decree on how more area is added. The actual change of 2x is the horizontal and vertical strip. The corner represents a change from the vertical strip interfering with the horizontal one. It's area, sure, but it won't be added on this step.
I imagine a square that grows by two strips, melts to absorb the area (forming a larger square), then grows again, then melts, and so on. The square isn't "staying still" long enough to have the horizontal and vertical extensions interact.
Practical conclusion: We've can take knowingly-flawed measurement ($$$f'(x) \sim 2x + dx$$$), and deduce the result it points to ($$$f'(x) = 2x$$$). The theories of exactly how we throw away $$$dx$$$ aren't necessary to master today. The key is realizing there are measurement artifacts that can be removed when modeling how pattern changes.