4. Learning The Official Terms
We've been able to describe our step-by-step process with analogies (X-Rays, Time-lapses, and rings) and diagrams:
However, this is a very elaborate way to communicate. Here's the Official Math® terms:
| Intuitive Concept | Formal Name | Symbol |
|---|---|---|
| X-Ray (split apart) | Take the derivative (differentiate) | $$\frac{d}{dr}$$ |
| Time-lapse (glue together) | Take the integral (integrate) | $$ \int $$ |
| Arrow direction | Integrate or take derivative "with respect to" a variable. | $$$dr$$$ implies moving along $$$r$$$ |
| Arrow start/stop | Bounds or range of integration | $$\int_{start}^{end} $$ |
| Slice | Integrand (shape being glued together, such as a ring) | Equation, such as $$$2 \pi r$$$ |
Let's walk through the fancy names.
The Derivative
The derivative is splitting a shape into slices as we move along a path (i.e., X-Raying it). Now here's the trick: although the derivative generates the entire sequence of slices (the black line), we can also extract a single slice.
Think about a function like $$$f(x) = x^2$$$. It's a curve that describes a giant list of possibilities (1, 4, 9, 16, 25, etc.). We can graph the entire curve, sure, or examine the value of f(x) at a specific value, like $$$x = 3$$$.
The derivative is similar. Officially, it's the entire pattern of slices, but we can zero into a specific slice by asking for the derivative at a certain value. (The derivative is a function, just like $$$f(x) = x^2$$$; if not otherwise specified, we're describing the entire function.)
What do we need to find the derivative? The shape to split apart, and the path to follow as we slice it up (the orange arrow). For example:
- The derivative of a circle with respect to the radius creates rings
- The derivative of a circle with respect to the perimeter creates slices
- The derivative of a circle with respect to the x-axis creates boards
I agree that "with respect to" sounds formal: Honorable Grand Poombah radius, it is with respect to you that we take the derivative. Math is a gentleman's game, I suppose.
Taking the derivative is also called "differentiating", because we are finding the difference between successive positions as a shape grows. (As we grow the radius of a circle, the difference between the current disc and the next size up is that outer ring.)
The Integral, Arrows, and Slices
The integral is glueing together (time-lapsing) a set of slices and measuring the final result. For example, we glued together the rings (into a "ring triangle") and saw it accumulated to $$$\pi r^2$$$, aka the area of a circle.
Here's what we need to find the integral:
- Which direction are we gluing the steps together? Along the orange line (the radius, in this case)
- When do we start and stop? At the start and end of the arrow (we start at 0, no radius, and move to r, the full radius)
- How big is each step? Well… each item is a "ring". Isn't that enough?
Nope! We need to be specific. We've been saying we cut a circle into "rings" or "pizza slices" or "boards". But that's not specific enough; it's like a BBQ recipe that says "Cook meat. Flavor to taste."
Maybe an expert knows what to do, but we need more specifics. How large, exactly, is each step (technically called the "integrand")?

Ah. A few notes about the variables:
- If we are moving along the radius $$$r$$$, then $$$dr$$$ is the little chunk of radius in the current step
- The height of the ring is the circumference, or $$$2 \pi r $$$
There's several gotchas to keep in mind.
First, $$$dr$$$ is its own variable, and not "d times r". It represents the tiny section of the radius present in the current step. This symbol ($$$dr$$$, $$$dx$$$, etc.) is often separated from the integrand by just a space, and it's assumed to be multiplied (written $$$2 \pi r \ dr$$$).
Next, if $$$r$$$ is the only variable used in the integral, then $$$dr$$$ is assumed to be there. So if you see $$$\int 2 \pi r$$$ this still implies we're doing the full $$$\int 2 \pi r \ dr$$$. (Again, if there are two variables involved, like radius and perimeter, you need to clarify which step we're using: $$$dr$$$ or $$$dp$$$?)
Last, remember that $$$r$$$ (the radius) changes as we time-lapse, starting at 0 and eventually reaching its final value. When we see $$$r$$$ in the context of a step, it means "the size of the radius at the current step" and not the final value it may ultimately have.
These issues are extremely confusing. I'd prefer we use rdr to indicate an intermediate "r at the current step" instead of a general-purpose "r" that's easily confused with the max value of the radius. I can't change the symbols at this point, unfortunately.
Practicing The Lingo
Let's learn to talk like calculus natives. Here's how we can describe our X-Ray strategies:
| Intuitive Visualization | Formal description | Symbol |
|---|---|---|
 |
take derivative of area of a circle with respect to the radius |
$$\frac{d}{dr} Area $$ |
 |
take derivative of area of a circle with respect to the perimeter |
$$\frac{d}{dp} Area $$ |
 |
take derivative of area of a circle with respect to the x-axis |
$$\frac{d}{dx} Area $$ |
Remember, the derivative just splits the shape into (hopefully) easy-to-measure steps, such as rings of size $$$2 \pi r \ dr$$$. We broke apart our lego set and have pieces scattered on the floor. We still need an integral to glue the parts together and measure the new size. The two commands are a tag team:
- The derivative says: "Ok, I split the shape apart for you. It looks like a bunch of pieces $$$2 \pi r$$$ tall and $$$dr$$$ wide."
- The integral says: "Oh, those pieces resemble a triangle -- I can measure that! The total area of that triangle is $$$\frac{1}{2} base \cdot height$$$, which works out to $$$\pi r^2$$$ in this case.".
Here's how we'd write the integrals to measure the steps we've made:
| Formal description | Symbol | Measures Total Size Of |
|---|---|---|
integrate 2 * pi * r * dr from r=0 to r=r |
$$\int_{0}^{r} 2 \pi r \ dr$$ |  |
integrate [a pizza slice] from [p = min perimeter] to [p = max perimeter] |
$$ \int_{p=min}^{p=max} (pizza \ slice) \ dp $$ |  |
integrate [a board] from [x = min value] to [x = max value] |
$$ \int_{x=min}^{x=max} board \ dx $$ | 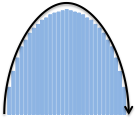 |
A few notes:
-
Often, we write an integrand as an unspecified "pizza slice" or "board" (use a formal-sounding name like $$$s(p)$$$ or $$$b(x)$$$ if you like). First, we setup the integral, and then we worry about the exact formula for a board or slice.
-
Because each integral represents slices from our original circle, we know they will be the same. Gluing any set of slices should always return the total area, right?
-
The integral is often described as "the area under the curve". It's accurate, but shortsighted. Yes, we are gluing together the slices under the curve. But this completely overlooks the preceding X-Ray and Time-Lapse thinking. Why are we dealing with set of slices or curve in the first place? Most likely, because those slices are easier than analyzing the shape itself (how do you "directly" measure a circle?).
Questions
1) Can you think of another activity which is made simpler by shortcuts and notation, vs. written English?
2) Interested in performance? Let's drive the calculus car, even if you can't build it yet.
Question 1: How would you write the integrals that cover half of a circle?
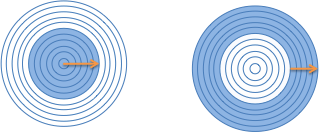
Each should would be similar to:
integrate [size of step] from [start] to [end] with respect to [path variable]
(Answer for the first half and the second half. This links to Wolfram Alpha, an online calculator, and we'll learn to use it later on.)
Question 2: Can you find the complete way to describe our "pizza-slice" approach?
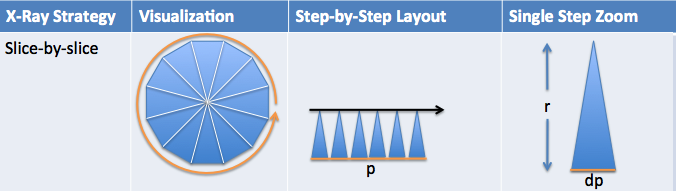
The "math command" should be something like this:
integrate [size of step] from [start] to [end] with respect to [path variable]
Remember that each slice is basically a triangle (so what's the area?). The slices move around the perimeter (where does it start and stop?). Have a guess for the command? Here it is, the slice-by-slice description.
Question 3: Can you figure out how to move from volume to surface area?
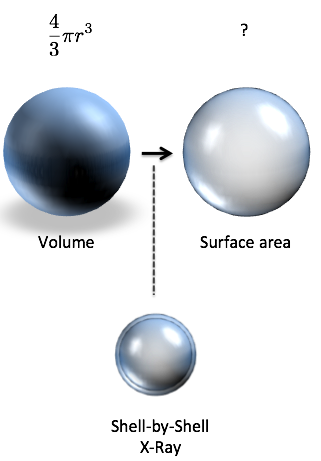
Assume we know the volume of a sphere is 4/3 * pi * r^3. Think about the instructions to separate that volume into a sequence of shells. Which variable are we moving through?
take derivative of [equation] with respect to [path variable]
Have a guess? Great. Here's the command to turn volume into surface area.