1. Calculus In A Few Minutes
Welcome to the Calculus course! Before we start, just a quick note about the intuition-first learning approach.
Move From Blurry To Sharp
What's a better learning strategy: full detail from start-to-finish, or progressively sharpening a quick overview?

The linear, official, approach doesn't work for me. Seeing a rough outline and improving it keeps our interest, and aware of how individual details are connected.
Move from Appreciation To Performance
Do you need to be a musician to enjoy a song? No way. There's a few levels of music understanding:
- Appreciation: being able to enjoy music
- Natural Description: being able to hum a tune you heard or thought of
- Symbolic Description: being able to read and write the sheet music for a song
- Performance: being able to play music with the official instruments (i.e., not your mouth)
- Theory: being able to explain why harmonies work, or melodies sound somber, joyous, etc.
Math knowledge is the same. Start by appreciating, even enjoying, the idea. Describe it with your own words, in English. Then, learn the official symbols to make communication easier ("2 + 3 = 5" is better than "Two plus three equals five", right?).
When we're ready, we can "perform" math by doing the calculations ourselves, and diving into the detailed theory. But only if you want! Decide for yourself what level of understanding you'd like to reach.
Move Through History
Many courses present the modern interpretation of math without looking at its origins.
Calculus was made by Newton to work out the laws of physics, right? Not exactly.
It was Archimedes, drawing shapes in the sand, who laid the foundations by imagining how circles and spheres were connected. He took shapes, morphed them, split them into tiny parts, and discovered connections through painstaking years of effort.
We're going to recreate his life's work in this course, in hours, using our calculus understanding. Geometry is a nice starting point because it's tangible and easy to visualize. (Physics? Not so much.)
Calculus In 1 Minute: Use X-Ray and Time-Lapse Vision
We usually take shapes, formulas, and situations at face value. Calculus gives us two superpowers to dig deeper:
-
X-Ray Vision: You see the hidden pieces inside a pattern. You don't just see the tree, you know it's made of rings, with another growing as we speak. (image source)

-
Time-Lapse Vision: You see the future path of an object laid out before you (cool, right?). "Hey, there's the moon. For the next few days it'll be white, but on the sixth it'll be low in the sky, in a color I like. I'll take a photo then." (image source)

So why is Calculus useful? Well, just imagine having X-Ray or Time-Lapse vision to use at will. That object over there, how was it put together? What will happen to it?
(Strangely, my letters to Marvel about Calculus-man have been ignored to date.)
Calculus In 10 Minutes: See Patterns Step-By-Step
What do X-Ray and Time-Lapse vision have in common? They examine patterns step-by-step. An X-Ray shows the individual slices inside, and a time-lapse puts each future state next to the other.
This seems pretty abstract. Let's look at a few famous patterns:
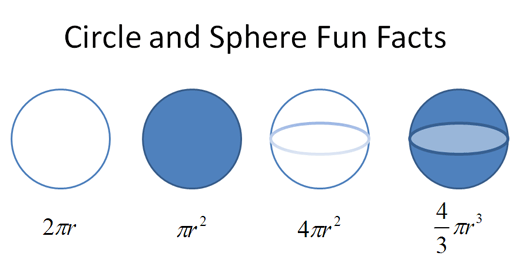
We have a vague feeling these formulas are connected, right?
Let's turn our X-Ray vision and see where this leads. Suppose we know the equation for circumference ($$$2 \pi r$$$) and want to figure out the equation for area. What can we do?
This is a tough question. Squares are easy to measure, but what can we do with an ever-curving shape?
Calculus to the rescue. Let's use our X-Ray vision to realize a disc is really just a bunch of rings put together. Similar to a tree trunk, here's a "step-by-step" view of a filled-in circle:
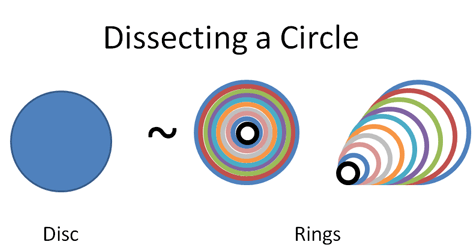
Why does this viewpoint help? Well, let's unroll those curled-up rings so they're easier to measure:
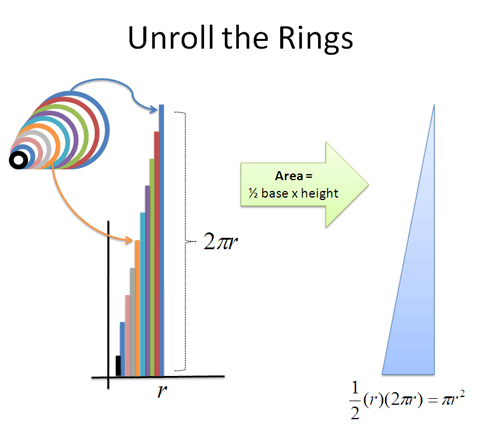
Whoa! We have a bunch of straightened rings that form a triangle, which is much easier to measure (Wikipedia has an animation).
The height of the largest ring is the full circumference ($$$2 \pi r$$$), and each ring gets smaller. The height of each ring depends on its original distance from the center; the ring 3 inches from the center has a height of $$$2 \pi \cdot 3$$$ inches. The smallest ring is a pinpoint, more or less, without any height at all.
And because triangles are easier to measure than circles, finding the area isn't too much trouble. The area of the “ring triangle” = $$$\frac{1}{2} base \cdot height = \frac{1}{2} r (2 \pi r) = \pi r^2$$$, which is the formula for a circle's area!
Our X-Ray vision revealed a simple, easy-to-measure structure within a curvy shape. We realized a circle and a set of glued-together rings were really the same. From another perspective, a filled-in disc is the "time lapse" of a ring that got larger and larger.
Remember learning arithmetic? We learned a few things to do with numbers (and equations): add/subtract, multiply/divide, and use exponents/roots. Not a bad start.
Calculus gives us two new options: split apart and glue together. A key epiphany of calculus is that our existing patterns can be seen as a bunch of glued-together pieces. It's like staring at a building and knowing it was made brick-by-brick.
So… What Can I Do With Calculus?
It depends. What can you do with arithmetic?
Technically, we don't need numbers. Our caveman ancestors did fine (well, for some version of "fine"). But having an idea of quantity makes the world a lot easier. You don't have a "big" and "small" pile of rocks: you have an exact count. You don't need to describe your mood as "good" or "great" -- you can explain your mood from 1 to 10.
Arithmetic provides universal metaphors that go beyond computation, and once seen, they're difficult to give up.
Calculus is similar: it's a step-by-step view of the world. Do we need X-Ray and Time Lapse vision all the time? Nope. But they're nice perspectives to "turn on" when we face a puzzling situation. What steps got us here? What's the next thing that will happen? Where does our future path lead?
There are specific rules to calculus, just like there are rules to arithmetic. And they're quite useful when you're cranking through an equation. But don't forget there are general notions of "quantity" and "step-by-step thinking" that we can bring everywhere.
Our primary goal is to feel what a calculus perspective is like (What Would Archimedes Do?). Over time, we'll work up to using the specific rules ourselves.
Questions
There's no real "homework", just a few questions to make sure things clicked:
1) What's your grandma-friendly explanation (or for grandpa, a child, a friend...) of what you've learned?
2) How'd the lesson go? Any aha! moments or areas to clarify?
You can leave your responses in the comment section below. Thanks!