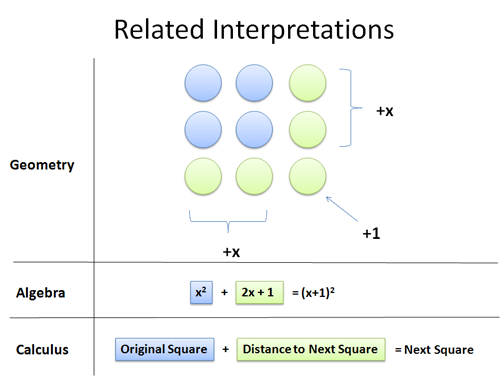
A reader recently suggested I write about modular arithmetic (aka “taking the remainder”). I hadn’t given it much thought, but realized the modulo is extremely powerful: it should be in our mental toolbox next to addition and multiplication.
Instead of hitting you in the face with formulas, let’s explore an idea we’ve been subtly exposed to for years. There’s a nice article on modular arithmetic that inspired this post.
Odd, Even and Threeven
Shortly after discovering whole numbers (1, 2, 3, 4, 5…) we realized they fall into two groups:
- Even: divisible by 2 (0, 2, 4, 6..)
- Odd: not divisible by 2 (1, 3, 5, 7…)
Why’s this distinction important? It’s the beginning of abstraction — we’re noticing the properties of a number (like being even or odd) and not just the number itself (“37”).
This is huge — it lets us explore math at a deeper level and find relationships between types of numbers, not specific ones. For example, we can make rules like this:
- Even x Even = Even
- Odd x Odd = Odd
- Even x Odd = Even
These rules are general — they work at the property level. (Intuitively, I have a chemical analogy that “evenness” is a molecule some numbers have, and cannot be removed by multiplication.)
But even/odd is a very specific property: division by 2. What about the number 3? How about this:
- “Threeven” means a number is divisbile by 3 (0, 3, 6, 9…)
- “Throdd” means you are not divisible by 3 (1, 2, 4, 5, 7, 8…)
Weird, but workable. You’ll notice a few things: there’s two types of throdd. A number like “4” is 1 away from being threeven (remainder 1), while the number 5 is two away (remainder 2).
Being “threeven” is just another property of a number. Perhaps not as immediately useful as even/odd, but it’s there: we can make rules like “threeven x threeven = threeven” and so on.
But it’s getting crazy. We can’t make new words all the time.
Enter the Modulo
The modulo operation (abbreviated “mod”, or “%” in many programming languages) is the remainder when dividing. For example, “5 mod 3 = 2” which means 2 is the remainder when you divide 5 by 3.
Converting everyday terms to math, an “even number” is one where it’s “0 mod 2” — that is, it has a remainder of 0 when divided by 2. An odd number is “1 mod 2” (has remainder 1).
Why’s this cool? Well, our “odd/even” rules become this:
- Even x Even = 0 x 0 = 0 [even]
- Odd x Odd = 1 x 1 = 1 [odd]
- Even x Odd = 0 x 1 = 0 [even]
Cool, huh? Pretty easy to work out — we converted “properties” into actual equations and found some new facts.
What’s even x even x odd x odd? Well, it’s 0 x 0 x 1 x 1 = 0. In fact, you can see if there’s an even being multiplied anywhere the entire result is going to be zero… I mean even :).
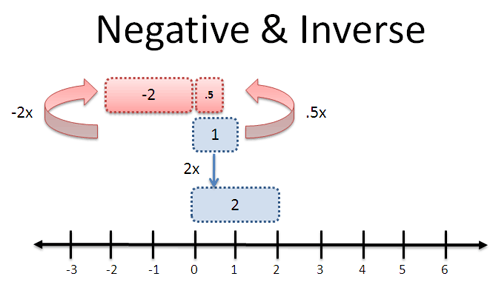
Clock Math
The sneaky thing about modular math is we’ve already been using it for keeping time — sometimes called “clock arithmetic”.
For example: it’s 7:00 (am/pm doesn’t matter). Where will the hour hand be in 7 hours?
Hrm. 7 + 7 = 14, but we can’t show “14:00” on a clock. So it must be 2. We do this reasoning intuitively, and in math terms:
- (7 + 7) mod 12 = (14) mod 12 = 2 mod 12 [2 is the remainder when 14 is divided by 12]
The equation “14 mod 12 = 2 mod 12” means, “14 o’clock” and “2 o’clock” look the same on a 12-hour clock. They are congruent, indicated by a triple-equals sign: 14 ≡ 2 mod 12.
Another example: it’s 8:00. Where will the big hand be in 25 hours?
Instead of adding 25 to 8, you might realize that 25 hours is just “1 day + 1 hour”. So, the clock will end up 1 hour ahead, at 9:00.
- (8 + 25) mod 12 ≡ (8) mod 12 + (25) mod 12 ≡ (8) mod 12 + (1) mod 12 ≡ 9 mod 12
You intuitively converted 25 to 1, and added that to 8.
Fun Property: Math just works
Using clocks as an analogy, we can figure out whether the rules of modular arithmetic “just work” (they do).
Addition/Subtraction
Let’s say two times look the same on our clock (“2:00” and “14:00”). If we add the same “x” hours to both, what happens?
Well, they change to the same amount on the clock! 2:00 + 5 hours ≡ 14:00 + 5 hours — both will show 7:00.
Why? Well, we never cared about the excess “12:00” that the 14 was carrying around. We can just add 5 to the 2 remainder that both have, and they advance the same. For all congruent numbers (2 and 14), adding and subtracting has the same result.
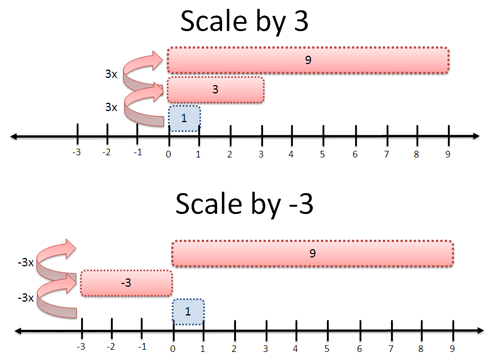
Multiplication
It’s harder to see whether multiplication stays the same. If 14 ≡ 2 (mod 12), can we multiply both sides and get the same result?
Let’s see — what happens when we multiply by 3?
Well, 2:00 * 3 ≡ 6:00. But what’s “14:00” * 3?
Remember, 14 = 12 + 2. So, we can say
- 14 * 3 = (12 + 2) * 3 = (12 * 3) + (2 * 3) mod 12
The first part (12 * 3) can be ignored! The “12 hour overflow” that 14 is carrying around just gets repeated a few times. But who cares? We ignore the overflow anyway.
When multiplying, it’s only the remainder that matters, which is the same 2 hours for 14:00 and 2:00. Intuitively, this is how I see that multiplication doesn’t change relationships with modular math (you can multiply both sides of a modular relationship and get the same result). See the above link for more rigorous proofs — these are my intuitive pencil lines.
Uses Of Modular Arithmetic
Now the fun part — why is modular arithmetic useful?
Simple time calculations
We do this intuitively, but it’s nice to give it a name. You have a flight arriving at 3pm. It’s getting delayed 14 hours. What time will it land?
Well, 14 ≡ 2 mod 12. So I think of it as “2 hours and an am/pm switch”, so I know it will be “3 + 2 = 5am”.
This is a bit more involved than a plain modulo operator, but the principle is the same.
Putting Items In Random Groups
Suppose you have people who bought movie tickets, with a confirmation number. You want to divide them into 2 groups.
What do you do? “Odds over here, evens over there”. You don’t need to know how many tickets were issued (first half, second half), everyone can figure out their group instantly (without contacting a central authority), and the scheme works as more people buy tickets.
Need 3 groups? Divide by 3 and take the remainder (aka mod 3). You’ll have groups “0”, “1” and “2”.
In programming, taking the modulo is how you can fit items into a hash table: if your table has N entries, convert the item key to a number, do mod N, and put the item in that bucket (perhaps keeping a linked list there). As your hash table grows in size, you can recompute the modulo for the keys.
Picking A Random Item
I use the modulo in real life. Really. We have 4 people playing a game and need to pick someone to go first. Play the mod N mini-game! Give people numbers 0, 1, 2, and 3.
Now everyone goes “one, two, three, shoot!” and puts out a random number of fingers. Add them up and divide by 4 — whoever gets the remainder exactly goes first. (For example: if the sum of fingers is 11, whoever had “3” gets to go first, since 11 mod 4 = 3).
It’s fast and it works.
Running Tasks On A Cycle
Suppose tasks need to happen on a certain schedule:
- Task A runs 3x/hour
- Task B runs 6x/hour
- Task C runs 1x/hour
How do you store this information and make a schedule? One way:
- Have a timer running every minute (keep track of the minute as “n”)
- 3x / hour means once every 60/3 = 20 minutes. So task A runs whenever “n % 20 == 0”
- Task B runs whenever “n % 10 == 0”
- Task C runs whenever “n % 60 == 0”
Oh, you need task C1 which runs 1x per hour, but not the same time as task C? Sure, have it run when “n mod 60 == 1” (still once per hour, but not the same as C1).
Mentally I see a cycle I want to “hit” at various intervals, so I insert a mod. The neat thing is that the hits can overlap independently. It’s a bit like XOR in that regard (each XOR can be layered — but that’s another article!).
Similarly, when programming you can print every 100th log item by doing: if (n % 100 == 0){ print… }.
It’s a very flexible, simple way to have items run on a schedule. In fact, it’s the way to answer the FizzBuzz sanity check. If you don’t have the modulo operation in your batbelt the question becomes much more tricky.
Finding Properties Of Numbers
Suppose I told you this:
What can you deduce quickly? Well, “a” must be even, since it’s equal to something which involves multiplication by 2.
If I also told you:
You’d balk. Not because you “know” the two products are different, but because one is clearly even, and the other is odd. There’s a problem: a can’t be the same number in both since the properties don’t match up.
Things like “even”, “threeven” and “mod n” are properties that are more general than individual numbers, and which we can check for consistency. So we can use modulo to figure out whether numbers are consistent, without knowing what they are!
If I tell you this:
Can these equations be solved with the integers? Let’s see:
- 3a + 5b = 8… let’s “mod 3 it”: 0 + 2b ≡ 2 mod 3, or b ≡ 1 mod 3
- 3a + b = 2… let’s “mod 3 it”: 0 + b ≡ 2 mod 3), or b ≡ 2 mod 3
A contradication, good fellows! B can’t be both “1 mod 3” and “2 mod 3” — it’s as absurd as being even and odd at the same time!
But there’s one gotcha: numbers like “1.5” are neither even nor odd — they aren’t integers! The modular properties apply to integers, so what we can say is that b cannot be an integer.
Because, in fact, we can solve that equation:
- (3a + 5b) – (3a +b) = 8 – 2
- 4b = 6
- b = 1.5
- 3a + 1.5 = 2, so 3a = 0.5, and a = 1/6
Don’t get seduced by the power of modulo! Know its limits: it applies to integers.
Cryptography
Playing with numbers has very important uses in cryptography. It’s too much to cover here, but modulo is used in Diffie-Hellman Key Exchange — used in setting up SSL connections to encrypt web traffic.
Plain English
Geeks love to use technical words in regular contexts. You might hear “X is the same as Y modulo Z” which means roughly “Ignoring Z, X and Y are the same.”
For example:
- b and B are identical, modulo capitalization
- The iTouch and iPad are identical, modulo size ;)
Onward and Upward
It’s strange thinking about the “utility” of the modulo operator — it’s like someone asking why exponents are useful. In everyday life, not very, but it’s a tool to understand patterns in the world, and create your own.
In general, I see a few general use cases:
- Range reducer: take an input, mod N, and you have a number from 0 to N-1.
- Group assigner: take an input, mod N, and you have it tagged as a group from 0 to N-1. This group can be agreed upon by any number of parties — for example, different servers that know N = 20 can agree what group ID=57 belongs to.
- Property deducer: treat numbers according to properties (even, threeven, and so on) and work out principles derived at the property level
I’m sure there’s dozens more uses I’ve missed — feel free to comment below. Happy math!
![]()