A math teacher recently asked how to explain the concept of subtracting negative numbers to her class. Why is 8 - (-6) = 14 the same as 8 + 6 = 14?
I've long internalized negatives as "opposite" and subtraction as "opposite of addition" so in my head, I had a notion of "opposite of opposite of addition" which simplifies down to "addition".
But that inner verbalization was still pretty abstract. After thinking of a better intuition, here was my reply:
Great question! I had to think about it for a bit. Addition and subtraction are related, but slightly different, than positive and negative numbers.
Imagine going on a walk. You're facing forward, and take 8 steps forward. This is really:
0 + 8
0 is your starting point. The "+" means "facing forward" and "8" means "8 steps in the direction you're facing". Ok.
Now, let's say we want to keep facing forward and take 6 more steps. That'd be:
8 + 6 = 14
Which gives us 14 steps from our starting point. What if we had faced backwards and took 6 steps?
8 - 6 = 2
Which means we're pretty close to our starting point, just 2 steps away. What if we had faced backwards but walked backwards 6 steps?
8 - (-6) = 14
Ah! The addition/subtraction tells us which way to face, and the positive/negative tells us if our steps will be forward or backward (regardless of the way we're facing).
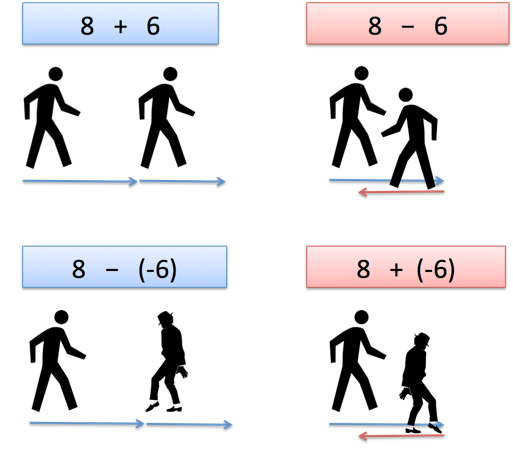
In a sense, the addition/subtraction acts as a verb ("face forward" or "face backward"), and the positive/negative acts as an adjective ("regular steps" or "backwards steps"). Or maybe it's an adverb, modifying how we walk (walk forwardly, walk backwardly). You get the idea.
For older students, "subtracting a negative" can be seen as "cancelling a debt". If I have a debt of \$30, and someone "subtracts it", I've effectively gained \$30. In general, if you remove a disadvantage, you have improved your situation -- a positive.
These explanations are a bit abstract, the walking one is more fun to try directly. I actually walked around while thinking through the intuition. (If you're adventurous, you might start thinking about taking side steps, or jumping, and how that would be represented.)
Happy math.
Appendix
When doing simple arithmetic, we only track the final location, not orientation. Facing backwards and walking backwards might have us looking at 0 while we advance forward. But mathematically, our endpoint is the same: 8 - (-6) = 8 + 6 = 14.
If we care about the way we're facing, we need a more complex math object (a vector) to keep track of our orientation as well as position ("14, facing forward" vs. "14, facing backward"). Perhaps we'd use a line integral, moving along a path and tracking the direction we face as we go.
A fitting analogy leads to questions about what else is possible.
Other Posts In This Series
- Techniques for Adding the Numbers 1 to 100
- Rethinking Arithmetic: A Visual Guide
- Quick Insight: Intuitive Meaning of Division
- Quick Insight: Subtracting Negative Numbers
- Surprising Patterns in the Square Numbers (1, 4, 9, 16…)
- Fun With Modular Arithmetic
- Learning How to Count (Avoiding The Fencepost Problem)
- A Quirky Introduction To Number Systems
- Another Look at Prime Numbers
- Intuition For The Golden Ratio
- Different Interpretations for the Number Zero