Summary: The Golden Ratio is special because it perfectly balances addition and multiplication.
The Golden Ratio (1.618...) is often presented with an air of mysticism as "the perfect proportion". Setting aside whether we can find the Golden Ratio in the leaves of a nearby houseplant, what makes it special from a math perspective?
Well, let's try to make a pattern that's as balanced (symmetric) as possible.
A quick guess is something like 1, 1, 1, 1, 1. Every item is identical, but it's not very interesting -- it's a song where every word is the same. Does it rhyme? Yeah. Do I care? Not really.
Ok, let's try 1, 2, 3, 4, 5. There's a symmetry in the relationship that every element is one more than the previous. But if we skip around to random elements, there's no real connection: what do 3, 8, and 17 have in common?
Ok, fine. What about 1, 2, 4, 8, 16? Each element is twice the previous, and all the numbers are clean powers of two. But... what about addition? Can we create new elements in our pattern from the previous ones?
- 1 + 2 = 3 [not quite 4...]
- 1 + 2 + 4 = 7 [not quite 8...]
- 1 + 2 + 4 + 8 = 15 [not quite 16...]
Argh. We can concoct a rule for addition ("Every element is the sum of all previous elements... plus an extra 1"), but that's not clean and you know it. Let's figure this out.
Symmetry Between Addition and Multiplication
Our goal is a pattern that's connected with both addition and multiplication. No varying number of additions, no cute "+1" on the end. Just a clean, simple relationship.
First off, we need to make every item connected by multiplication. We need powers:
1 x x^2 x^3 x^4
Whatever number the pattern uses (x), everything will be a power of it (just like 1, 2, 4, 8, although that sequence wasn't symmetric enough).
Next, we need an "addition symmetry" that connects the items. Every element should be buildable from the previous ones without extra rules. Throwing a few ideas against the wall:
- Can we have
1 + x = x? If we subtract x from both sides, that leads to 1 = 0. Uh oh, we're breaking math. - How about
1 + 1 = x? Maybe we can allow multiple copies of everything. But that's just another way of getting x=2, you sneak. - How about
1 + x = 1? Ack, that just implies x = 0.0, 0, 0, 0is symmetric but not interesting.
Hrm. The next addition pattern that might make sense is 1 + x = x^2. If we follow this idea, here's what happens:
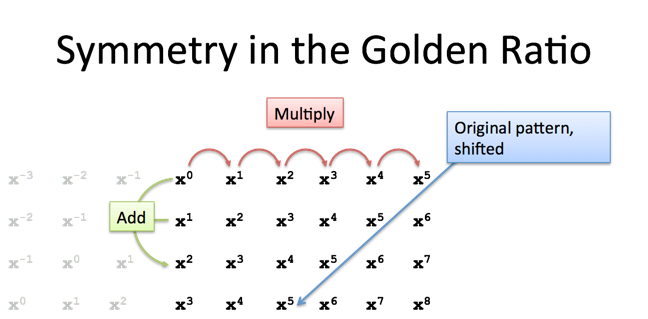
A few notes:
- Starting from a single connection
1 + x = x^2, we can multiply through byxand getx + x^2 = x^3. Every element is made from the previous two. - $x^0$ is another way to write 1. Makes the pattern easier to see, I think.
- Everything in the pattern grid is just our original pattern, shifted a bit. Neat.
Ok. That's the goal for the pattern, let's try to solve it.
![]()
![]()
We can find the "x" that makes this relationship true using the quadratic formula:
![]()
Plugging in a=1, b=-1, and c=-1, we get:
![]()
We only want a positive solution (the new part can't be negative), so we have
![]()
We label the solution Phi ($\phi$).
You can see it happening below. There are slight differences as the decimals go on -- computers have fixed precision.
Visualize the Intuition
Many descriptions of the Golden Ratio describe splitting a whole into parts, each of which is in the golden ratio:
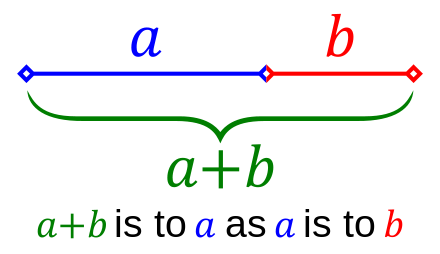
I prefer the "growth factor" scenario, where we start with a single item (1.0) and evolve it, while keeping it linked to its ancestors with both arithmetic and multiplication. Just describing a ratio doesn't call out the symmetry we're able to achieve.
Visually, I see a growing blob, like this:
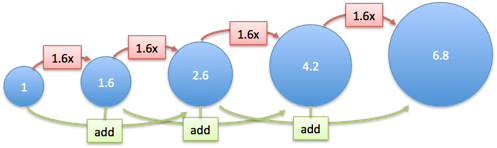
As we scale by Phi each time (1.618) we get:
- Addition symmetry: Each element is the sum of the previous two
- Multiplication symmetry: Each element is a scaled version of the previous
- Growth symmetry: Addition and multiplication change the pattern identically
Aha! That's a nice combo if I ever saw one. The "growing blob" can represent the length of a line, a 2d shape, an angle -- which can lead to interesting patterns:

The key relationship is we move from one blob to the next, such that multiplication and addition have the same effect:
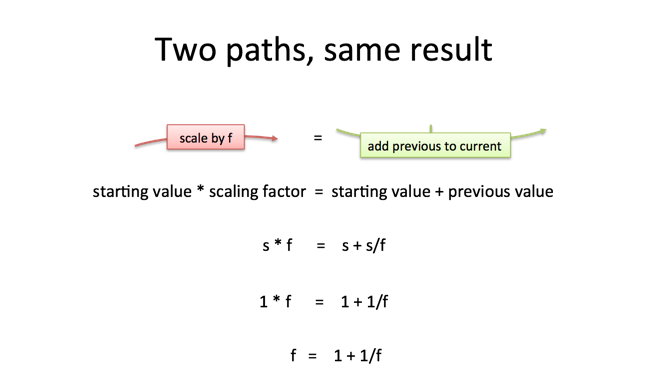
We've described the Golden Ratio with different phrasing: the scaling factor (f) must equal the original (1) plus the previous item (1/f). We divide by our growth factor to find the previous element given the current one.
Solving $f = 1 + \frac{1}{f}$ yields the Golden Ratio as before.
Is the Golden Ratio Everywhere?
The Golden Ratio tends to be oversold in its occurrences. While it may appear occasionally in nature, buildings, and portraits, if you draw lines thick enough many things have a ratio of about 1.5 to 1.
I think the deeper intuition comes from realizing we've made addition and multiplication symmetric.
The Fibonacci sequence is built from having every piece built from the two before:
Using a certain formula, we can jump to a Fibonacci number by repeated scaling (exponents) instead of laboriously adding the parts. And maybe we'd come to expect the Golden Ratio here, since it's the scaling factor that allows two parts to add to the next item in the sequence. (The specifics of dividing by $\sqrt 5$ are because we need to adjust based on the starting pieces.)
Rather than hunting for examples of the Golden Ratio in the produce aisle, let's soak in the beauty of balancing the forces of multiplication and addition.
Happy math.
Other Posts In This Series
- Techniques for Adding the Numbers 1 to 100
- Rethinking Arithmetic: A Visual Guide
- Quick Insight: Intuitive Meaning of Division
- Quick Insight: Subtracting Negative Numbers
- Surprising Patterns in the Square Numbers (1, 4, 9, 16…)
- Fun With Modular Arithmetic
- Learning How to Count (Avoiding The Fencepost Problem)
- A Quirky Introduction To Number Systems
- Another Look at Prime Numbers
- Intuition For The Golden Ratio
- Different Interpretations for the Number Zero