While working on some math colorizations I ran across some interpretations of division.
Multiplication can be repeated addition, scaling, rotating (via imaginary numbers), and more.
What about division? Let's take a look.
The permutation formula lets us pick 3 items out of 10, in a specific order. To order 3 items from 10, we have 10 options for the first choice, 9 options for the second, and 8 for the third, giving us 10 _ 9 _ 8 = 720 possibilities.
But how is this process written in most math books?
![]()
What's going on?
Well, we just want a portion of the factorial. 10! gives the full sequence (10 _ 9 _ 8 _ 7 _ 6 _ 5 _ 4 _ 3 _ 2 _ 1), but we want to stop it after we hit 8. That means we divide by 7!. The only part that's not removed is 10 _ 9 * 8.
In this case, division is acting like a brake/boundary/filter that stops the factorial from running hog-wild. (They get out of control, you know.)

Ah! If writing a software program, you wouldn't actually compute 10!, 7! and do a division. What if we needed 3 choices from 1000 options? (1000 factorial has 2568 digits and will make your computer cry. I told you this would happen!)
If we realize the role of division as a boundary marker, we can just compute 1000 _ 999 _ 998 = 997,002,000 and call it a day.
Let's keep going.
Suppose we don't care about the order of the items we pick: ABC is the same as CBA. What to do?
Well, we can apply another division! This time, we don't want a boundary, but want to merge/consolidate/group up similar items. Everything that looks like ABC (e.g., ACB, BAC, BCA, CAB, CBA) should be counted once.
With 3 items there are 3! rearrangements, so the final count is 720/3! = 720/6 = 120 choices.
As a formula:

Neat, right? The division in the permutation formula acts as a boundary, and the division in the combination formula is a type of "group up". I imagine the variations being merged into a single option:
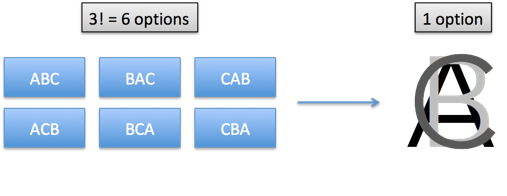
The words we pick frame how we think about an equation. "Divide" implies we're splitting things apart. If we know alternate meanings (repeated subtraction, boundaries, consolidation), we may pick a better description. Saying "divide by k!" doesn't have the same intuition as "consolidate the reorderings".
I think math concepts are fundamentally simple but their written description may not be. (Ever try to describe how to put on a shirt?) The goal is finding the words to make the idea click.
Happy math.
Other Posts In This Series
- Techniques for Adding the Numbers 1 to 100
- Rethinking Arithmetic: A Visual Guide
- Quick Insight: Intuitive Meaning of Division
- Quick Insight: Subtracting Negative Numbers
- Surprising Patterns in the Square Numbers (1, 4, 9, 16…)
- Fun With Modular Arithmetic
- Learning How to Count (Avoiding The Fencepost Problem)
- A Quirky Introduction To Number Systems
- Another Look at Prime Numbers
- Intuition For The Golden Ratio
- Different Interpretations for the Number Zero