Taking two vectors, we can write every combination of components in a grid:
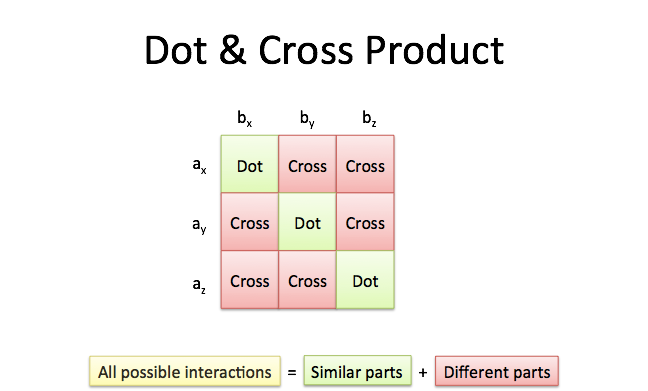
This completed grid is the outer product, which can be separated into the:
Dot product, the interactions between similar dimensions (
x*x,y*y,z*z)Cross product, the interactions between different dimensions (
x*y,y*z,z*x, etc.)
The dot product ($\vec{a} \cdot \vec{b}$) measures similarity because it only accumulates interactions in matching dimensions. It’s a simple calculation with 3 components.
The cross product (written $\vec{a} \times \vec{b}$) has to measure a half-dozen “cross interactions”. The calculation looks complex but the concept is simple: accumulate 6 individual differences for the total difference.
Instead of thinking “When do I need the cross product?” think “When do I need interactions between different dimensions?”.
Area, for example, is formed by vectors pointing in different directions (the more orthogonal, the better). Indeed, the cross product measures the area spanned by two 3d vectors (source):

(The “cross product” assumes 3d vectors, but the concept extends to higher dimensions.)
Did the key intuition click? Let’s hop into the details.
Defining the Cross Product
The dot product represents the similarity between vectors as a single number:
![]()
For example, we can say that North and East are 0% similar since $(0, 1) \cdot (1, 0) = 0$. Or that North and Northeast are 70% similar ($\cos(45) = .707$, remember that trig functions are percentages.) The similarity shows the amount of one vector that “shows up” in the other.
Should the cross product, the difference between vectors, be a single number too?
Let’s try. Sine is the percentage difference, so we could write:
![]()
Unfortunately, we’re missing some details. Let’s say we’re looking down the x-axis: both y and z point 100% away from us. A number like “100%” tells us there’s a big difference, but we don’t know what it is! We need extra information to tell us “the difference between $\vec{x}$ and $\vec{y}$ is this” and “the difference between $\vec{x}$ and $\vec{z}$ is that“.
So, let’s express the cross product as a vector:
The size of the cross product is the numeric “amount of difference” (with $\sin(\theta)$ as the percentage). By itself, this doesn’t distinguish $\vec{x} \times \vec{y}$ from $\vec{x} \times \vec{z}$.
The direction of the cross product is based on both inputs: it’s the direction orthogonal to both (i.e., favoring neither).
Now $\vec{x} \times \vec{y}$ and $\vec{x} \times \vec{z}$ have different results, each with a magnitude indicating they are “100%” different from $\vec{x}$.
(Should the dot product be a vector result too? Well, we’re tracking the similarity between $\vec{a}$ and $\vec{b}$. The similarity measures the overlap between the original vector directions, which we already have.)
Geometric Interpretation
Two vectors determine a plane, and the cross product points in a direction different from both (source):

Here’s the problem: there’s two perpendicular directions. By convention, we assume a “right-handed system” (source):
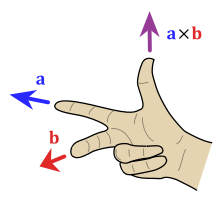
If you hold your first two fingers like the diagram shows, your thumb will point in the direction of the cross product. I make sure the orientation is correct by sweeping my first finger from $\vec{a}$ to $\vec{b}$. With the direction figured out, the magnitude of the cross product is $|a| |b| \sin(\theta)$, which is proportional to the magnitude of each vector and the “difference percentage” (sine).
The Cross Product For Orthogonal Vectors
To remember the right hand rule, write the xyz order twice: xyzxyz. Next, find the pattern you’re looking for:
xy => z(xcrossyisz)yz => x(ycrosszisx; we looped around:ytoztox)zx => y
Now, xy and yx have opposite signs because they are forward and backward in our xyzxyz setup.
So, without a formula, you should be able to calculate:
![]()
Again, this is because x cross y is positive z in a right-handed coordinate system. I used unit vectors, but we could scale the terms:
![]()
Calculating The Cross Product
A single vector can be decomposed into its 3 orthogonal parts:
![]()
![]()
When the vectors are crossed, each pair of orthogonal components (like $a_x \times b_y$) casts a vote for where the orthogonal vector should point. 6 components, 6 votes, and their total is the cross product. (Similar to the gradient, where each axis casts a vote for the direction of greatest increase.)
xy => zandyx => -z(assume $\vec{a}$ is first, soxymeans $a_x b_y$)yz => xandzy => -xzx => yandxz => -y
xy and yx fight it out in the z direction. If those terms are equal, such as in $(2, 1, 0) \times (2, 1, 1)$, there is no cross product component in the z direction (2 – 2 = 0).
The final combination is:
![]()
where $\vec{n}$ is the unit vector normal to $\vec{a}$ and $\vec{b}$.
Don’t let this scare you:
- There’s 6 terms, 3 positive and 3 negative
- Two dimensions vote on the third (so the
zterm must only haveyandxcomponents) - The positive/negative order is based on the
xyzxyzpattern
If you like, there is an algebraic proof, that the formula is both orthogonal and of size $|a| |b| \sin(\theta)$, but I like the “proportional voting” intuition.
Example Time
Again, we should do simple cross products in our head:
![]()
Why? We crossed the x and y axes, giving us z (or $\vec{i} \times \vec{j} = \vec{k}$, using those unit vectors). Crossing the other way gives $-\vec{k}$.
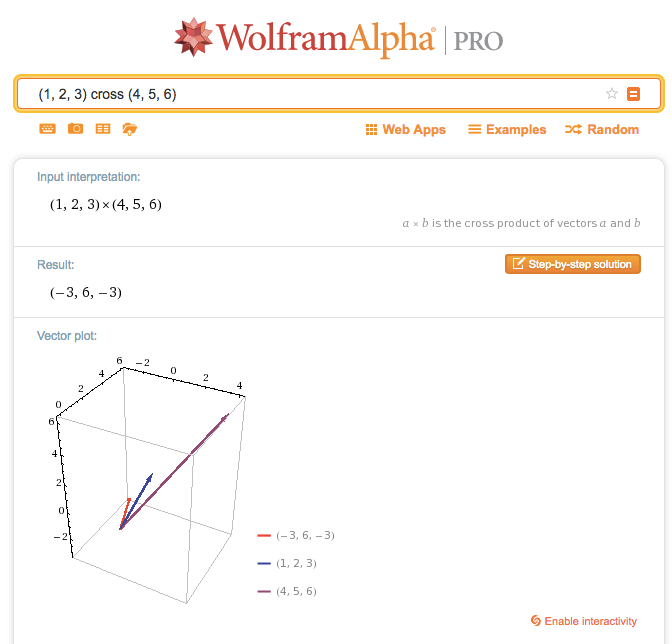
Here’s how I walk through more complex examples:
![]()
- Let’s do the last term, the z-component. That’s (1)(5) minus (4)(2), or 5 – 8 = -3. I did
zfirst because it usesxandy, the first two terms. Try seeing (1)(5) as “forward” as you scan from the first vector to the second, and (4)(2) as backwards as you move from the second vector to the first. - Now the
ycomponent: (3)(4) – (6)(1) = 12 – 6 = 6 - Now the
xcomponent: (2)(6) – (5)(3) = 12 – 15 = -3
So, the total is $(-3, 6, -3)$ which we can verify with Wolfram Alpha.
In short:
- The cross product tracks all the “cross interactions” between dimensions
- There are 6 interactions (2 in each dimension), with signs based on the
xyzxyzorder
Appendix
Connection with the Determinant
You can calculate the cross product using the determinant of this matrix:
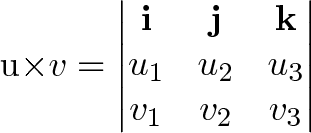
![]()
There’s a neat connection here, as the determinant (“signed area/volume”) tracks the contributions from orthogonal components.
There are theoretical reasons why the cross product (as an orthogonal vector) is only available in 0, 1, 3 or 7 dimensions. However, the cross product as a single number is essentially the determinant (a signed area, volume, or hypervolume as a scalar).
Connection with Curl
Curl measures the twisting force a vector field applies to a point, and is measured with a vector perpendicular to the surface. Whenever you hear “perpendicular vector” start thinking “cross product”.
We take the “determinant” of this matrix:
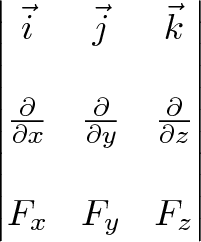
![]()
Instead of multiplication, the interaction is taking a partial derivative. As before, the $\vec{i}$ component of curl is based on the vectors and derivatives in the $\vec{j}$ and $\vec{k}$ directions.
Relation to the Pythagorean Theorem
The cross and dot product are like the orthogonal sides of a triangle:
![]()
For unit vectors, where $|a| = |b| = 1 $, we have:
![]()
I cheated a bit in the grid diagram, as we have to track the squared magnitudes (as done in the Pythagorean Theorem).
Advanced Math
The cross product & friends get extended in Clifford Algebra and Geometric Algebra. I’m still learning these.
Cross Products of Cross Products
Sometimes you’ll have a scenario like:
![]()
First, the cross product isn’t associative: order matters.
Next, remember what the cross product is doing: finding orthogonal vectors. If any two components are parallel ($\vec{a}$ parallel to $\vec{b}$) then there are no dimensions pushing on each other, and the cross product is zero (which carries through to $0 \times \vec{c}$).
But it’s ok for $\vec{a}$ and $\vec{c}$ to be parallel, since they are never directly involved in a cross product, for example:
![]()
Whoa! How’d we get back to $\vec{j}$? We asked for a direction perpendicular to both $\vec{i}$ and $\vec{j}$, and made that direction perpendicular to $\vec{i}$ again. Being “doubly perpendicular” means you’re back on the original axis.
Dot Product of Cross Products
Now if we take
![]()
what happens? We’re forced to do $\vec{a} \times \vec{b}$ first, because $\vec{b} \cdot \vec{c}$ returns a scalar (single number) which can’t be used in a cross product.
If $\vec{a}$ and $\vec{c}$ are parallel, what happens? Well, $\vec{a} \times \vec{b}$ is perpendicular to $\vec{a}$, which means it’s perpendicular to $\vec{c}$, so the dot product with $\vec{c}$ will be zero.
I never really memorized these rules, I have to think through the interactions.
Other Coordinate Systems
The Unity game engine is left-handed, OpenGL (and most math/physics tools) are right-handed. Why?
In a computer game, x goes horizontal, y goes vertical, and z goes “into the screen”. This results in a left-handed system. (Try it: using your right hand, you can see x cross y should point out of the screen).
Applications of the Cross Product
- Find the direction perpendicular to two given vectors.
- Find the signed area spanned by two vectors.
- Determine if two vectors are orthogonal (checking for a dot product of 0 is likely faster though).
- “Multiply” two vectors when only perpendicular cross-terms make a contribution (such as finding torque).
- With the quaternions (4d complex numbers), the cross product performs the work of rotating one vector around another (another article in the works!).
Happy math.
Other Posts In This Series
- Vector Calculus: Understanding the Dot Product
- Vector Calculus: Understanding the Cross Product
- Vector Calculus: Understanding Flux
- Vector Calculus: Understanding Divergence
- Vector Calculus: Understanding Circulation and Curl
- Vector Calculus: Understanding the Gradient
- Understanding Pythagorean Distance and the Gradient