Circulation is the amount of force that pushes along a closed boundary or path. It's the total "push" you get when going along a path, such as a circle.
A vector field is usually the source of the circulation. If you had a paper boat in a whirlpool, the circulation would be the amount of force that pushed it along as it went in a circle. The more circulation, the more pushing force you have.
Curl is simply the circulation per unit area, circulation density, or rate of rotation (amount of twisting at a single point). Imagine shrinking your whirlpool down smaller and smaller while keeping the force the same: you'll have a lot of power in a small area, so will have a large curl. If you widen the whirlpool while keeping the force the same as before, then you'll have a smaller curl. And of course, zero circulation means zero curl.
Intuition
Circulation is the amount of "pushing" force along a path. Curl is the amount of pushing, twisting, or turning force when you shrink the path down to a single point. Let's use water as an example.
Suppose we have a flow of water and we want to determine if it has curl or not: is there any twisting or pushing force? To test this, we put a paddle wheel into the water and notice if it turns (the paddle is vertical, sticking out of the water like a revolving door -- not like a paddlewheel boat):
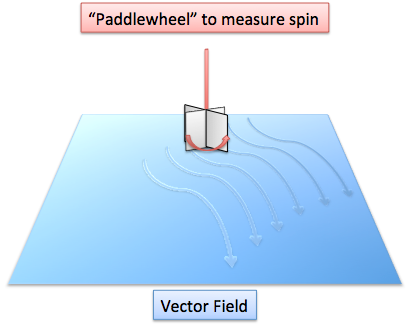
If the paddle does turn, it means this field has curl at that point. If it doesn't turn, then there's no curl.
What does it really mean if the paddle turns? Well, it means the water is pushing harder on one side than the other, making it twist. The larger the difference, the more forceful the twist and the bigger the curl. Also, a turning paddle wheel indicates that the field is "uneven" and not symmetric; if the field were even, then it would push on all sides equally and the paddle wouldn't turn at all.
The fact that there is a "twist" means the field is not conservative (this has nothing to do with its political views).
A conservative field is "fair" in the sense that work needed to move from point A to point B, along any path, is the same. For example, consider a river: its field is conservative. Sure, you can get a free ride downstream, but then you have to do work to get back to your starting point. Or, you can do work to move upstream, and get a free ride back. Either way, the amount of work you "put in" is the same as what you get back.
However, in a field with curl (like a whirlpool), you can get a free ride by moving in the direction of the twist. In a whirlpool, you can get a free trip by moving with the current in a circle. If you fight the current and go the wrong way, you have to use energy with no free ride at all.
Conservative fields have zero curl: there are no free twists to push you along. Alternatively, if a field has curl, it is not conservative.
Gravity is another example of a conservative field. Technically, if you lift a rock and then let it fall, the energy you get from falling is the same as what you put in to lift the rock. Theoretically speaking, no energy was gained or lost in this transaction.
Additional Details
To be technical, curl is a vector, which means it has a both a magnitude and a direction. The magnitude is simply the amount of twisting force at a point.
The direction is a little more tricky: it's the orientation of the axis of your paddlewheel in order to get maximum rotation. In other words, it is the direction which will give you the most "free work" from the field. Imagine putting your paddlewheel sideways in the whirlpool - it wouldn't turn at all. If you put it in the proper direction, it begins turning.
But wait a minute -- aren't there two directions to get a twisting motion? Couldn't you just turn the paddlewheel "upside down" and get the maximum curl as well?
Yep, you're right. By convention alone, if the paddle wheel is rotating counterclockwise, its curl vector points out of the page. This is a type of right-hand rule: make a fist with your right hand and stick out your thumb. If the circulation/pushing force follows the twisting of your fingers (counterclockwise), then the curl vector will be in the direction of your thumb.
Mathematics
Circulation is the integral of a vector field along a path - you are adding how much the field "pushes" you along a path.
How do we find this? Well, we should expect some type of dot product, because we want to know the amount that one vector (the force) is pushing in the direction of another (the path). So, the two vectors we need are (1) the path vector and (2) the field vector at every point along the path.
If we have a function that defines the position at any time, $F(t)$, we can take the time derivative to get the velocity at that position.
The velocity vector is always in the direction of movement -- if you are moving from A to B, the velocity vector will be an arrow from A to B, i.e. your change in position or your direction of movement. So, we can use the velocity to get our direction.
It's important to understand why we aren't using the position vector itself -- it tells us where we are, but not where we're going. We need to know our direction to see how much "push" we are getting: Knowing your position in a river isn't important -- are you going upstream or downstream, and at what angle?
The force vector (2) is defined by the field we are in. No derivatives or other changes are necessary -- every point in the field has some force acting on it.
So, our formula for circulation is:
![]()
![]()
![]()
Remember, velocity is simply the derivative of position (r), so (dr) is a vector giving us our direction. We integrate along the entire path and use the dot product to see how much pushing force is applied. We then sum up these "pushes" to get the total circulation.
Since curl is the circulation per unit area, we can take the circulation for a small area (letting the area shrink to 0). However, since curl is a vector, we need to give it a direction -- the direction is normal (perpendicular) to the surface with the vector field. The magnitude is the same as before: circulation/area.
Recall that by convention (a bunch of people agreeing), counterclockwise circulation will give a curl pointing out of the page. Using these facts, we can create the formula for curl:
![]()
Where (S) is the surface we are considering; the direction of the curl is the normal to the surface.
You'll see fancier equations for curl where the surface shrinks to zero (such as in wikipedia), but recognize the basic intuition -- curl is the circulation per unit area.
Parting Thoughts
You'll often see curl of a field (F) written like this:
![]()
which is a cross-product of the gradient and the field (F). This has to do with how curl is actually computed, which will be material for another article (and probably in your textbook already -- see wikipedia for details).
If I have been successful, you should understand intuitively what circulation and curl mean, and how we got the formulae above. They spring up naturally from our definition of circulation as "pushing force along a path" and curl as "pushing force/area".
Math should be a tool for clearly stating what we already know. Understand the intuition and then tackle the complicated formulas. Happy math.
PS. Have some fun and check out this video of a famous whirlpool. Imagine the circulation on this (go on, imagine):
Other Posts In This Series
- Vector Calculus: Understanding the Dot Product
- Vector Calculus: Understanding the Cross Product
- Vector Calculus: Understanding Flux
- Vector Calculus: Understanding Divergence
- Vector Calculus: Understanding Circulation and Curl
- Vector Calculus: Understanding the Gradient
- Understanding Pythagorean Distance and the Gradient