Intuitive Guide to Angles, Degrees and Radians

It’s an obvious fact that circles should have 360 degrees. Right?

Wrong. Most of us have no idea why there’s 360 degrees in a circle. We memorize a magic number as the “size of a circle” and set ourselves up for confusion when studying advanced math or physics, with their so called “radians”.

“Radians make math easier!” the experts say, without a simple reason why (discussions involving Taylor series are not simple). Today we’ll uncover what radians really are, and the intuitive reason they make math easier.

Where do degrees come from?

Before numbers and language we had the stars. Ancient civilizations used astronomy to mark the seasons, predict the future, and appease the gods (when making human sacrifices, they’d better be on time).

How is this relevant to angles? Well, bub, riddle me this: isn’t it strange that a circle has 360 degrees and a year has 365 days?. And isn’t it weird that constellations just happen to circle the sky during the course of a year?

Unlike a pirate, I bet you landlubbers can’t determine the seasons by the night sky. Here’s the Big Dipper (Great Bear) as seen from New York City in 2008 (try any city):

constellation rotation

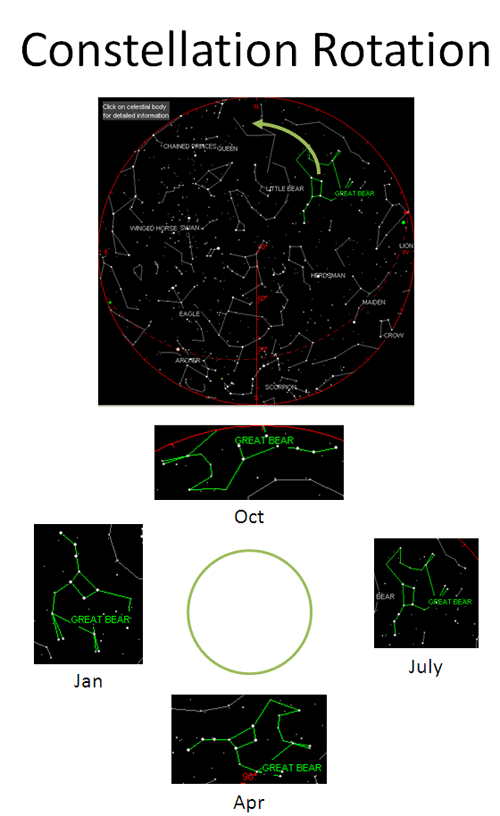
Constellations make a circle every day (video). If you look at the same time every day (midnight), they will make a circle throughout the year. Here’s a theory about how degrees came to pass:

Humans noticed that constellations moved in a full circle every year
Every day, they were off by a tiny bit (”a degree”)
Since a year has about 360 days, a circle had 360 degrees

But, but… why not 365 degrees in a circle?

Cut ‘em some slack: they had sundials and didn’t know a year should have a convenient 365.242199 degrees like you do.

360 is close enough for government work. It fits nicely into the Babylonian base-60 number system, and divides well (by 2, 3, 4, 6, 10, 12, 15, 30, 45, 90… you get the idea).

Basing mathematics on the Sun seems perfectly reasonable

Earth lucked out: ~360 is a great number of days to have in a year. But it does seem arbitrary: on Mars we’d have roughly ~680 degrees in a circle, for the longer Martian year (Martian days are longer too, but you get the idea). And in parts of Europe they’ve used gradians, where you divide a circle into 400 pieces.

Many explanations stop here saying, “Well, the degree is arbitrary but we need to pick some number.” Not here: we’ll see that the entire premise of the degree is backwards.

Radians Rule, Degrees Drool

A degree is the amount I, an observer, need to tilt my head to see you, the mover. It’s a tad self-centered, don’t you think?

Suppose you saw a friend go running on a large track:

“Hey Bill, how far did you go?”
“Well, I had a really good pace, I think I went 6 or 7 mile–”
“Shuddup. How far did I turn my head to see you move?”
“What?”
“I’ll use small words for you. Me in middle of track. You ran around. How…much…did…I…turn…my…head?”
“Jerk.”

Selfish, right? That’s how we do math! We write equations in terms of “Hey, how far did I turn my head see that planet/pendulum/wheel move?”. I bet you’ve never bothered to think about the pendulum’s feelings, hopes and dreams.

Do you think the equations of physics should be made simple for the mover or observer?

Radians: The Unselfish Choice

Much of physics (and life!) involves leaving your reference frame and seeing things from another’s viewpoint. Instead of wondering how far we tilted our heads, consider how far the other person moved.

Degrees vs radians

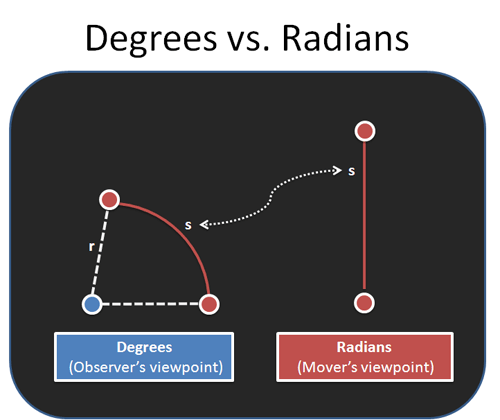
Degrees measure angles by how far we tilted our heads. Radians measure angles by distance traveled.

But absolute distance isn’t that useful, since going 10 miles is a different number of laps depending on the track. So we divide by radius to get a normalized angle:

$\displaystyle{Radian = \frac{distance \hspace{10pt} traveled}{radius}}$

You’ll often see this as $\displaystyle{\theta = \frac{s}{r}}$ , or angle in radians = arc length divided by radius.

A circle has 360 degrees or 2pi radians — going all the way around is 2*pi*r / r. So a radian is about 360/2*pi or 57.3 degrees.

Now don’t be like me, memorizing this thinking “Great, another unit. 57.3 degrees is so weird.” Because it is weird when you’re still thinking about you!

Moving 1 radian (unit) is a perfectly normal distance to travel. Put another way, our idea of a “clean, 90 degree angle” means the mover goes a very unclean pi/2 units. Think about it — “Hey Bill, can you run 90 degrees for me? What’s that? Oh, yeah, that’d be pi/2 miles from your point of view.” The strangeness goes both ways.

Radians are the empathetic way to do math — a shift from away from head tilting and towards the mover’s perspective.

Strictly speaking, radians are a ratio (length divided by another length) and don’t have a dimension. Practically speaking, we’re not math robots, and it helps to think of radians as “distance traveled on a unit circle”.

Using Radians

I’m still getting used to thinking in radians. But we encounter the concept of “mover’s distance” quite a bit:

We use “rotations per minute” not “degrees per second” when measuring certain rotational speeds. This is a shift towards the mover’s reference point (”How many laps has it gone?”) and away from an arbitrary degree measure.

When a satellite orbits the Earth, we understand its speed in “miles per hour”, not “degrees per hour”. Now divide by the distance to the satellite and you get the orbital speed in radians per hour.

Sine, that wonderful function, is defined in terms of radians as

$\displaystyle{sin(x) = x - \frac{x^3}{3!} + \frac{x^5}{5!} - \frac{x^7}{7!} ...}$

This formula only works when x is in radians! Why? Well, sine is fundamentally related to distance moved, not head-tilting. But we’ll save that discussion for another day.

Radian Example 1: Wheels of the bus

Let’s try a real example: you have a bus with wheels of radius 2 meters (it’s a monster truck bus). I’ll say how fast the wheels are turning and you say how fast the bus is moving. Ready?

“The wheels are turning 2000 degrees per second”. You’d think:

Ok, the wheels are going 2000 degrees per second. That means it’s turning 2000/360 or 5 and 5/9ths rotations per second. Circumference = 2 * pi * r, so it’s moving, um, 2 * 3.14 * 5 and 5/9ths… where’s my calculator…

“The wheels are turning 6 radians per second”. You’d think:

Radians are distance along a unit circle — we just scale by the real radius to see how far we’ve gone. 6 * 2 = 12 meters per second. Next question.

Wow! No crazy formulas, no pi floating around — just multiply to convert rotational speed to linear speed. All because radians speak in terms of the mover.

The reverse is easy too. Suppose you’re cruising 90 feet per second on the highway (60 miles per hour) on your 24″ inch rims (radius 1 foot). How fast are the wheels turning?

Well, 90 feet per second / 1 foot radius = 90 radians per second.

That was easy. I suspect rappers sing about 24″ rims for this very reason.

Radian Example 2: sin(x)

Time for a beefier example. Calculus is about many things, and one is what happens when numbers get really big or really small.

Choose a number of degrees (x), and put sin(x) into your calculator:

When you make x small, like .01, sin(x) gets small as well. And the ratio of sin(x)/x seems to be about .017 — what does that mean? Even stranger, what does it mean to multiply or divide by a degree? Can you have square or cubic degrees?

Radians to the rescue! Knowing they refer to distance traveled (they’re not just a ratio!), we can interpret the equation this way:

x is how far you traveled along a circle
sin(x) is how high on the circle you are

So sin(x)/x is the ratio of how high you are to how far you’ve gone: the amount of energy that went in an “upward” direction. If you move vertically, that ratio is 100%. If you move horizontally, that ratio is 0%.

sin x vs x

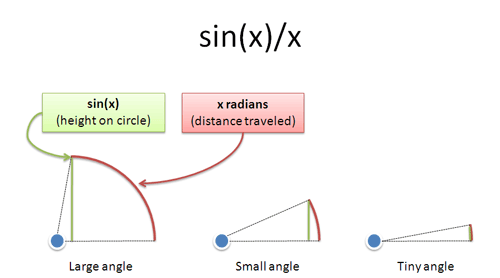
When something moves a tiny amount, such as 0 to 1 degree from our perspective, it’s basically going straight up. If you go an even smaller amount, from 0 to .00001 degrees, it’s really going straight up. The distance traveled (x) is very close to the height (sin(x)).

As x shrinks, the ratio gets closer to 100% — more motion is straight up. Radians help us see, intuitively, why sin(x)/x approaches 1 as x gets tiny. We’re just nudging along a tiny amount in a vertical direction. By the way, this also explains why sin(x) ~ x for small numbers.

Sure, you can rigorously prove this using calculus, but the radian intuition helps you understand it.

Remember, these relationships only work when measuring angles with radians. With degrees, you’re comparing your height on a circle (sin(x)) with how far some observer tilted their head (x degrees), and it gets ugly fast.

So what’s the point?

Degrees have their place: in our own lives, we’re the focal point and want to see how things affect us. How much do I tilt my telescope, spin my snowboard, or turn my steering wheel?

With natural laws, we’re an observer describing the motion of others. Radians are about them, not us. It took me many years to realize that:

Degrees are arbitrary because they’re based on the sun (365 days ~ 360 degrees), but they are backwards because they are from the observer’s perspective.
Because radians are in terms of the mover, equations “click into place”. Converting rotational to linear speed is easy, and ideas like sin(x)/x make sense.

Even angles can be seen from more than one viewpoint, and understanding radians makes math and physics equations more intuitive. Happy math.

41 Comments

Posted July 9, 2008, under Math
Tags:
Related Posts:

Intuitive Arithmetic With Complex Numbers

Explanations for everyone.

A Visual, Intuitive Guide to Imaginary Numbers

Rethinking Arithmetic: A Visual Guide

Advertise on BetterExplained.com

Like it? Share on:

RSS or Email Subscription |

Print This Post

Tools of the trade:

Don't Make Me Think
(Web Design)

On Writing Well
(Writing Style)

MS Office 2007
(Charts & Diagrams)

41 Comments »

Trackbacks & Pingbacks

Pingback by Ragged Clown » Blog Archive » Why Radians? — July 9, 2008 @ 8:58 pm
Pingback by Flying Colours Maths Blog » Angles: degrees and radians — January 24, 2009 @ 11:20 am
Pingback by Understanding Exponents (Why does 0^0 = 1?) | BetterExplained — February 17, 2009 @ 12:23 pm
Pingback by We Like This… | maths4edinburgh — May 5, 2009 @ 2:45 am
Pingback by Better Explained « Xavier Seton’s Blog — May 7, 2009 @ 12:39 am

Comments

Hi Khalid, I always enjoy your explanations.

While you’re talking about how arbitrary degrees are as a measure of angle, it reminded me of how radians are somewhat arbitrary. Here’s a really interesting article on how pi should actually be defined as what is currently 2 * pi:

http://www.math.utah.edu/~palais/pi.pdf

Tony — July 9, 2008 @ 9:39 am
Hi Tony, thanks for the comment! Yep, that’s a very interesting article.

I think radians are pretty natural (distance traveled/radius), but the scale is made somewhat arbitrary (as you say) based on our definition of pi. Perhaps it would be easier if a circle had pi radians instead of 2 pi (as a result of defining pi to be the circumference of a unit circle).

Kalid — July 9, 2008 @ 9:52 am
Shouldn’t the orbital speed of the satellite be the linear speed in mph divided by the distance from the center of the earth to the satellite (not the radius of the earth)?

Fredg — July 9, 2008 @ 10:28 am
@Fredg: Great catch! Yes, that was my mistake. Fixing it up now.

Kalid — July 9, 2008 @ 11:13 am
I’m a pilot. I can just imagine ATC telling me “Turn right heading pi radians.” Maybe they would just give me the coefficient and say turn right heading 1. Then north could be zero, east could be .5 etc. I can also imagine looking at my compass in the plane and seeing it marked with 0, 1/2pi, pi, 1 1/2 pi, 2pi, etc. Actually…no, I can’t imagine any of that at all.

Tracy R Reed — July 9, 2008 @ 11:32 am
@Tracy: Heh, point well taken — degrees are definitely best when we’re observing our own motion . Though a radian compass might be a fun gag.

Kalid — July 9, 2008 @ 12:37 pm
You are the only one I know who can make a math blog post sound funny!

Siya — July 9, 2008 @ 1:44 pm
Thanks Siya — I think there are gems hidden away in almost any topic .

Kalid — July 9, 2008 @ 8:31 pm
Kalid I can only encourage you to write faster and write more. I can’t get enough of these explanations.

Sid — July 10, 2008 @ 4:52 pm
Thanks for the encouragement Sid! I hope to increase the output too .

Kalid — July 10, 2008 @ 6:00 pm
HI KALID,
i am an comp sc grad. working for 15 yrs.
i love maths, but i had really bad maths teachers, all thru school and college.

as a result, i never understood what radians were for. THANKS A TON for this article. at last it is crystal clear.

av

av — July 10, 2008 @ 9:18 pm
Thanks av, glad it was helpful! It took me quite a while to figure out what radians were about as well .

Kalid — July 11, 2008 @ 12:02 am
Kalid,
Thank you again! I agree with the others. More!! That is all long as the quality stays the same and you have time to work out.

later
T.

T Rose — July 15, 2008 @ 7:31 am
Dear kalid,
Your site has rekindled my interest in Maths. thanks a lot.
Recently I had started assuming the following;
Degrees: Angle measured from origin
Radians: Angle measured from circumference (in terms of radius)
For equilateral triangle, the angle is 60 degrees between two sides. If these two sides are squeezed to form 57.3 degrees, third side bulges out to form an arc of a circle with 1 radian measurement.

Regards.
V.Manoharan

V.Manoharan — July 17, 2008 @ 7:46 am
@Mr. Rose: Thanks — yep, will definitely try to keep the quality up .

@V.Manoharan: Glad you enjoyed it. That’s an interesting thought — yes, an angle of 1 radian (about 57.3 degrees) will correspond to a bulge of length 1.

Kalid — July 22, 2008 @ 8:43 pm
hi khalid!

i m a student of 11th std, and i really hated maths before meeting you, but you are a real eye opener!!

P.S. i wish i had teachers like you in school!!!!

chirag — August 6, 2008 @ 9:01 am
(in continuation)…..
though i have become a great fan of yours, i just want to say that you should try to cover up topics a bit faster as you are my teacher from now onwards…..i m from india, and prep. for engineering….hope you consider it(covering up topics)…especially trigo. and quadratic equations, they are my least favourite(very tough)
thank you,
chirag

chirag — August 6, 2008 @ 9:16 am
Hi Chirag, thanks for the comment! Yep, math can be enjoyable if seen in the proper light.

I’ll try to keep cranking out posts as I can

Kalid — August 8, 2008 @ 12:52 pm
Your explanation of constellation rotation is incorrect. Every constellation rotates completely everyday. So if the Big Dipper is upside down it’ll be right side up in twelve hours. Now if you measure at the same time everyday each constellation will be one degree farther along than at the same time the day before and that is the once a year rotation. Your wikipedia reference has a succint description. “Ancient astronomers noticed that the stars in the sky, which circle the celestial pole every day, seem to advance in that circle by approximately one-360th of a circle, i.e., one degree, each day.”

Otherwise great post. Thanks.

joe — September 1, 2008 @ 11:46 pm
nice mathematics

Jessy — December 2, 2008 @ 2:51 am
Great explain thank you so much..

Uzaktan Eğitim — December 4, 2008 @ 4:02 am
pl. explain something about gradient curl & divergence. these are very difficult to understand

amit — December 18, 2008 @ 10:16 am
@Joe: Thanks for the clarification! I’ll update the article.

@Amit: You’re in luck, those topics are covered here: http://betterexplained.com/articles/category/math/vector-calculus/

Kalid — December 18, 2008 @ 8:18 pm
Obama needs to add you to the educational advisory board Your method of teaching definitely networks more of the mind enabling better recall and retention. I am sure that when Benjamin Franklin was creating the core of the current educational policies of this nation, this was way closer to the mark of what he intended then the holes in the head that we currently have.

anonymous — February 26, 2009 @ 5:47 pm
Thanx

Zrmbilisim Katkıları İle 2009 Seo Yarışması — March 20, 2009 @ 9:20 am
I have a question that I hope you can answer. When talking about a 360 degree circle, 90 degrees is vertical and 180 degrees is horizontal. Why is that different in cardinal directions? Example, 0 degrees is North. I am trying to understand the difference.

Thank you

Kim Frey

Kim Frey — April 5, 2009 @ 7:44 pm
@Anon: Thanks . Yes, I think there are many improvements we can make to how education is handled.

@Kim: Great question. I think the difference is in the starting reference point.

Mathematicians are used to thinking about the x and y axis, so going “right” on the x-axis is the natural starting point for them. Therefore +90 degrees means going “North” (or along the y-axis, as angles increase counter-clockwise for mathematicians).

In navigation (like hiking in the woods), North may be a more universal reference point — it’s where compasses point. In that case, +90 degrees means going East (since the angles increase clockwise).

It’s a bit confusing since each type of use has a different reference point, but thanks for asking.

Kalid — April 5, 2009 @ 9:34 pm
How do radians and degrees relate to sine space or sines? My understanding of sines is that you simply compute the ratio of the opposite/hypotenuse sides of a right triangle to derive the linear measurement. So can I infer that sines are also from the perspective of the “mover”; since you are dividing one length by another length? If so, would it be better to use sine space because you would have a dimension associated to your unit (cm, m, km, etc…). Maybe a discussion on how the right triangle relates to the unit circle would be helpful. Thanks for a great article!

E.G. — April 6, 2009 @ 4:04 pm
@E.G.: I’m not quite sure I understand the question, but here’s my take on how sine and radians relate.

Radians and degrees represent progress along a circle; 90 degrees represents a quarter-turn, and pi/2 radians represents the distance traveled when moving a quarter of the way around the circle.

Sine can mean many things, including the ratio of the sides of a right triangle. Another interpretation which may help is that sine represents the “height”, where 1.0 is the max height, -1.0 is the min height, and everything else is a fraction in-between.

(Edit: correcting an error in this comment):

The interesting thing is that sine/cosine represent position in grid coordinates, which the mover may not know about!

For example, 45 degrees represents a certain position along the circle. From the mover’s perspective, they are halfway to 90 (top of the circle), and indeed, they have moved halfway to their goal (at 45 degrees, the distance along the circumference from the start and top of the circle is the same).

But from our observer’s perspective, 45 degrees looks like a height of sin(45) or .707 — that is, at 45 degrees, the mover is 70.7% of the way to the top! In the last “half” they move the remaining amount. I see sine and cosine as ways for us to map the distance traveled in the mover’s frame of reference to distance traveled in ours.

Radians and degrees are different ways of describing how far you’ve traveled along the circle. Sine is a way to describing how ‘high’ you are on the circle (from our grid’s perspective), as a percentage of the maximum. Hope this helps!

Kalid — April 6, 2009 @ 8:41 pm
Thanks for the explanation. My intent was to understand the topic from a different perspective. Now I understand (”a ha”), thanks!

E.G.

E.G. — April 7, 2009 @ 6:49 pm
Awesome. you explained this better then my math teacher

Unshu — April 27, 2009 @ 5:45 pm
@E.G.: Thanks, always happy to share an a-ha moment .

@Unshu: Glad it was helpful!

Kalid — April 27, 2009 @ 7:01 pm
I finally got this radian stuff and thought I would sum up my brain blast for anyone who is still confused. This is a really basic explanation that just uses straight math.

Describing an angle in radians is just a way of writing an angle without the degree symbol.

The measure of an angle in radians is the ratio of the arc length it cuts out to the length of the circle’s radius.

If the arc that the angle cuts out is exactly equal to the length of the radius, the angle therefore has a measure of 1/1, 1 radian, or just 1.

Another useful example:
If the angle cuts out an arc that is equal to the whole circumference of the circle (2πr), the normal angle is 360 degrees, and so that means that the ratio of the arc length (2πr) to the radius is just 2πr/r, or 2π. This gives us the measure of the angle in radians, 2π.

In other words, 360 degrees = 2π radians,
180 degrees = π radians, and
180 degrees/π radians = 1.

We can use this ratio as a conversion factor.

To convert 39 degrees to radians, multiply 39 degrees x (π radians/180 degrees) to find that 39 degrees is really 39π/180 or about 0.68 radians!

I hope that helped!

George — September 13, 2009 @ 12:12 pm
I like math!

matematik — October 25, 2009 @ 2:52 pm
hey… ur explanation is really good. i have a presentation on radian angle tomorrow… do u knoe where i can find some more funda on radian???

i123 — October 27, 2009 @ 6:55 am
Hi Kalid I’m in grade 11 doing a college course supplied by our school and right now I think radians are the most stupid “number” in the world. Thanks for the explanation on what the stupid things are any way at least I’ll be able to understand part of it.

azariah007 — October 28, 2009 @ 12:42 am

RSS feed for comments on this post. TrackBack URI

Have a question? Know an explanation that caused your own a-ha moment? Write about it here.