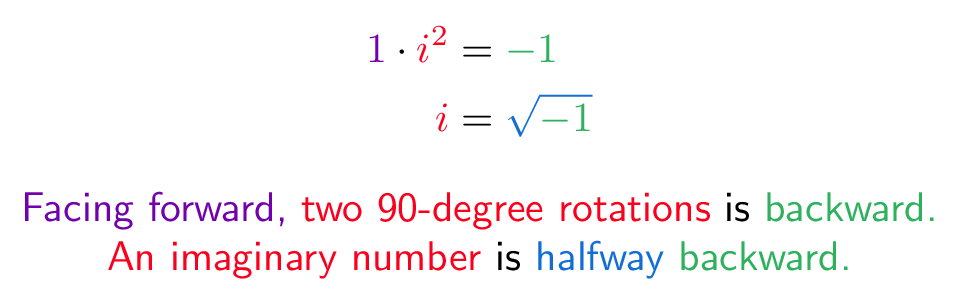Imaginary numbers have an intuitive explanation: they “rotate” numbers, just like negatives make a “mirror image” of a number. This insight makes arithmetic with complex numbers easier to understand, and is a great way to double-check your results. Here’s our cheatsheet:

complex arithmetic operations

This post will walk through the intuitive meanings.

Complex Variables

In regular algebra, we often say “x = 3″ and all is dandy — there’s some number “x”, whose value is 3. With complex numbers, there’s a gotcha: there’s two dimensions to talk about. When writing

\displaystyle{z = 3 + 4i}

complex number example

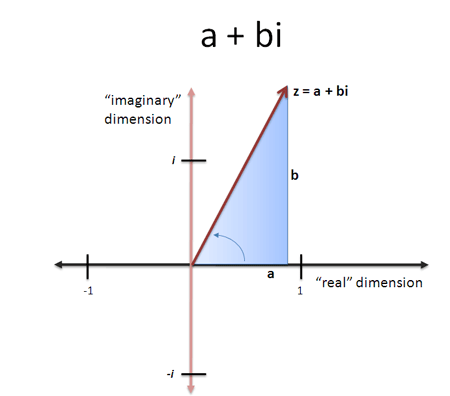
we’re saying there’s a number “z” with two parts: 3 (the real part) and 4i (imaginary part). It is a bit strange how “one” number can have two parts, but we’ve been doing this for a while. We often write:

\displaystyle{y = 3\frac{4}{10} = 3 + .4}

and it doesn’t bother us that a single number “y” has both an integer part (3) and a fractional part (.4 or 4/10). Y is a combination of the two. Complex numbers are similar: they have their real and imaginary parts “contained” in a single variable (shorthand is often Re and Im).

Unfortunately, we don’t have nice notation like (3.4) to “merge” the parts into a single number. I had an idea to write the imaginary part vertically, in fading ink, but it wasn’t very popular. So we’ll stick to the “a + bi” format.

Measuring Size

Because complex numbers use two independent axes, we find size (magnitude) using the Pythagorean Theorem:

complex magnitude

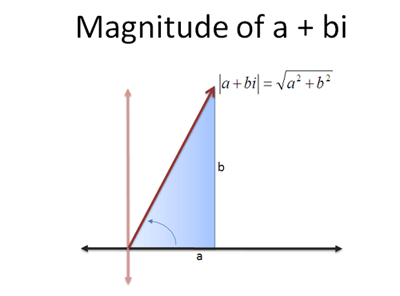
So, a number z = 3 + 4i would have a magnitude of 5. The shorthand for “magnitude of z” is this: |z|

See how it looks like the absolute value sign? Well, in a way, it is. Magnitude measures a complex number’s “distance from zero”, just like absolute value measures a negative number’s “distance from zero”.

Complex Addition and Subtraction

We’ve seen that regular addition can be thought of as “sliding” by a number. Addition with complex numbers is similar, but we can slide in two dimensions (real or imaginary). For example:

complex addition

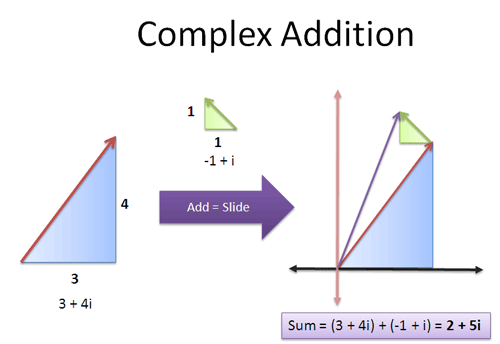
Adding (3 + 4i) to (-1 + i) gives 2 + 5i.

Again, this is a visual interpretation of how “independent components” are combined: we track the real and imaginary parts separately.

Subtraction is the reverse of addition — it’s sliding in the opposite direction. Subtracting (1 + i) is the same as adding -1 * (1 + i), or adding (-1 – i).

Complex Multiplication

Here’s where the math gets interesting. When we multiply two complex numbers (x and y) to get z:

  • Add the angles: angle(z) = angle(x) + angle(y)
  • Multiply the magnitudes: |z| = |x| * |y|

That is, the angle of z is the sum of the angles of x and y, and the magnitude of z is the product of the magnitudes. Believe it or not, the magic of complex numbers makes the math work out!

Multiplying by the magnitude (size) makes sense — we’re used to that happening in regular multiplication (3 × 4 means you multiply 3 by 4′s size). The reason the angle addition works is more detailed, and we’ll save it for another time. (Curious? Find the sine and cosine addition formulas and compare them to how (a + bi) * (c + di) get multiplied out).

Time for an example: let’s multiply z = 3 + 4i by itself. Before doing all the math, we know a few things:

  • The resulting magnitude will be 25. z has a magnitude of 5, so |z| * |z| = 25.
  • The resulting angle will be above 90. 3 + 4i is above 45 degrees (since 3 + 3i would be 45 degrees), so twice that angle will be more than 90.

With our predictions on paper, we can do the math:

\displaystyle{(3 + 4i) * (3 + 4i) = 9 + 16i^2 + 24i = -7 + 24i}

Time to check our results:

  • Magnitude: sqrt((-7 * -7) + (24 * 24)) = sqrt(625) = 25, which matches our guess.
  • Angle: Since -7 is negative and 24i is positive, we know we are going “backwards and up”, which means we’ve crossed 90 degrees (“straight up”). Getting geeky, we compute atan(24/-7) = 106.2 degrees (keeping in mind we’re in quadrant 2). This guess checks out too.

Nice. While we can always do the math out, the intuition about rotations and scaling helps us check the result. If the resulting angle was less than 90 (“forward and up”, for example), or the resulting magnitude not 25, we’d know there was a mistake in our math.

Complex Division

Division is the opposite of multiplication, just like subtraction is the opposite of addition. When dividing complex numbers (x divided by y), we:

  • Subtract angles angle(z) = angle(x) – angle(y)
  • Divide by magnitude |z| = |x| / |y|

Sounds good. Now let’s try to do it:

\displaystyle{\frac{3 + 4i}{1 + i}}

Hrm. Where to start? How do we actually do the division? Dividing regular algebraic numbers gives me the creeps, let alone weirdness of i (Mister mister! Didya know that 1/i = -i? Just multiply both sides by i and see for yourself! Eek.). Luckily there’s a shortcut.

Introducing Complex Conjugates

Our first goal of division is to subtract angles. How do we do this? Multiply by the opposite angle! This will “add” a negative angle, doing an angle subtraction.

complex conjugate example

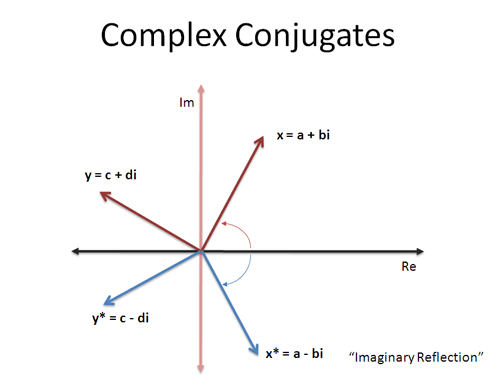
Instead of z = a + bi, think about a number z* = a – bi, called the “complex conjugate”. It has the same real part, but is the “mirror image” in the imaginary dimension. The conjugate or “imaginary reflection” has the same magnitude, but the opposite angle!

So, multiplying by a – bi is the same as subtracting an angle. Neato.

multiply complex conjugate

Complex conjugates are indicated by a star (z*) or bar above the number — mathematicians love to argue about these notational conventions. Either way, the conjugate is the complex number with the imaginary part flipped:

\displaystyle{z = a + bi}

Note that b doesn’t have to be “negative”. If z = 3 – 4i, then z* = 3 + 4i.

Multiplying By the Conjugate

What happens if you multiply by the conjugate? What is z times z*? Without thinking, think about this:

\displaystyle{z \cdot z^* = 1 \cdot z \cdot z^*}

So we take 1 (a real number), add angle(z), and add angle (z*). But this last angle is negative — it’s a subtraction! So our final result should be a real number, since we’ve canceled the angles. The number should be |z|^2 since we scaled by the size twice.

Now let’s do an example: \displaystyle{(3 + 4i) * (3 - 4i) = 9 - 16i^2 = 25}

We got a real number, like we expected! The math fans can try the algebra also:

\displaystyle{(a + bi) * (a - bi) = a^2 + abi - abi -b^2i^2 = a^2 + b^2 }

Tada! The result has no imaginary parts, and is the magnitude squared. Understanding complex conjugates as a “negative rotation” lets us predict these results in a different way.

Scaling Your Numbers

When multiplying by a conjugate z*, we scale by the magnitude |z*|. To reverse this effect we can divide by |z|, and to actually shrink by |z| we have to divide again. All in all, we have to divide by |z| * |z| to the original number after multiplying by the conjugate.

Show Me The Division!

I’ve been sidestepping the division, and here’s the magic. If we want to do

\displaystyle{\frac{3 + 4i}{1 + i}}

We can approach it intuitively:

  • Rotate by opposite angle: multiply by (1 – i) instead of (1 + i)
  • Divide by magnitude squared: divide by |sqrt(2)|^2 = 2

The answer, using this approach, is:

\displaystyle{\frac{3 + 4i}{1 + i} = (3 + 4i) \cdot (1 - i) \cdot \frac{1}{2} = (3 - 4i^2 + 4i - 3i) \cdot \frac{1}{2} = \frac{7}{2} + \frac{1}{2}i}

The more traditional “plug and chug” method is to multiply top and bottom by the complex conjugate:

\displaystyle{\frac{3 + 4i}{1 + i} = \frac{3 + 4i}{1 + i} \cdot \frac{1 - i}{1 - i} = \frac{3 - 4i^2 + 4i - 3i}{1 - i^2} = \frac{7 + i}{2}}

We’re traditionally taught to “just multiply both sides by the complex conjugate” without questioning what complex division really means. But not today.

We know what’s happening: division is subtracting an angle and shrinking the magnitude. By multiplying top and bottom by the conjugate, we subtract by the angle of (1-i), which happens to make the denominator a real number (it’s no coincidence, since it’s the exact opposite angle). We scaled both the top and bottom by the same amount, so the effects cancel. The result is to turn division into a multiplication in the numerator.

Both approaches work (you’re usually taught the second), but it’s nice to have one to double-check the other.

More Math Tricks

Now that we understand the conjugate, there’s a few properties to consider:

\displaystyle{(x + y)^* = x^* + y^*}

\displaystyle{(x \cdot y)^* = x^* \cdot y^*}

The first should make sense. Adding two numbers and “reflecting” (conjugating) the result, is the same as adding the reflections. Another way to think about it: sliding two numbers then taking the opposite, is the same as sliding both times in the opposite direction.

The second property is trickier. Sure, the algebra may work, but what’s the intuitive explanation?

The result (xy)* means:

  • Multiply the magnitudes: |x| * |y|
  • Add the angles and take the conjugate (opposite): angle(x) + angle(y) becomes “-angle(x) + -angle(y)”

And x* times y* means:

  • Multiply the magnitudes: |x| * |y| (this is the same as above)
  • Add the conjugate angles: angle(x) + angle(y) = -angle(x) + -angle(y)

Aha! We get the same angle and magnitude in each case, and we didn’t have to jump into the traditional algebra explanation. Algebra is fine, but it isn’t always the most satisfying explanation.

A Quick Example

The conjugate is a way to “undo” a rotation. Think about it this way:

  • I deposited $3, $10, $15.75 and $23.50 into my account. What transaction will cancel these out? To find the opposite: add them up, and multiply by -1.
  • I rotated a line by doing several multiplications: (3 + 4i), (1 + i), and (2 + 10i). What rotation will cancel these out? To find the opposite: multiply the complex numbers together, and take the conjugate of the result.

See the conjugate z* as a way to “cancel” the rotation effects of z, just like a negative number “cancels” the effects of addition. One caveat: with conjugates, you need to divide by |z| * |z| to remove the scaling effects as well.

Closing Thoughts

The math here isn’t new, but I never realized why complex conjugates worked as they did. Why a – bi and not -a + bi? Well, complex conjugates are not a random choice, but a mirror image from the imaginary perspective, with the exact opposite angle.

Seeing imaginary numbers as rotations gives us a new mindset to approach problems; the “plug and chug” formulas can make intuitive sense, even for a strange topic like complex numbers. Happy math.

Other Posts In This Series

  1. A Visual, Intuitive Guide to Imaginary Numbers
  2. Intuitive Arithmetic With Complex Numbers
  3. Understanding Why Complex Multiplication Works
  4. Intuitive Guide to Angles, Degrees and Radians
  5. Intuitive Understanding Of Euler's Formula
  6. An Interactive Guide To The Fourier Transform
  7. Intuitive Understanding of Sine Waves
  8. An Intuitive Guide to Linear Algebra