Understanding Exponents (Why does 0^0 = 1?)

We’re taught that exponents are repeated multiplication. This is a good introduction, but it breaks down on 3^1.5 and the brain-twisting 0^0. How do you repeat zero zero times and get 1?

You can’t, not while exponents are repeated multiplication. Today our mental model is due for an upgrade.

Viewing arithmetic as transformations

Let’s step back — how do we learn arithmetic? We’re taught that numbers are counts of something (fingers), addition is combining counts (3 + 4 = 7) and multiplication is repeated addition (2 times 3 = 2 + 2 + 2 = 6).

Repeated addition works when multiplying by nice round numbers like 2 and 10, but not when using numbers like -1 and $\sqrt{2}$. Why?

Our model was incomplete. Numbers aren’t just a count; a better viewpoint is a position on a line. This position can be negative (-1), between other numbers ($\sqrt{2}$), or in another dimension (i).

Arithmetic became a way to transform a number: Addition was sliding (+3 means slide 3 units to the right), and multiplication was scaling (times 3 means scale it up 3x).

So what are exponents?

Enter the Expand-o-tron(TM)

Let me introduce the Expand-o-tron 3000.

Yes, this device looks like a shoddy microwave — but instead of heating food, it grows numbers. Put a number in and a new one comes out. Here’s how:

Start with 1.0
Set the growth to the desired change after one second (2x, 3x, 10.3x)
Set the time to the number of seconds
Push the button

And shazam! The bell rings and we pull out our shiny new number. Suppose we want to change 1.0 into 9:

Put 1.0 in the expand-o-tron
Set the change for “3x” growth, and the time for 2 seconds
Push the button

The number starts transforming as soon as we begin: We see 1.0, 1.1, 1.2… and just as finish the first second, we’re at 3.0. But it keeps going: 3.1, 3.5, 4.0, 6.0, 7.5. As just as we finish the 2nd second we’re at 9.0. Behold our shiny new number!

Mathematically, the expand-o-tron (exponent function) does this:

$\displaystyle{\text{original} \cdot \text{growth}^{\text{duration}} = \text{new}}$

$\displaystyle{\text{growth}^{\text{duration}} = \frac{\text{new}}{\text{original}}}$

For example, 3^2 = 9/1. The base is the amount to grow each unit (3x), and the exponent is the amount of time (2). A formula like 2^n means “Use the expand-o-tron at 2x growth for n seconds”.

We always start with 1.0 in the expand-o-tron to see how it changes a single unit. If we want to see what would happen if we started with 3.0 in the expand-o-tron, we just scale up the final result. For example:

“Start with 1 and double 3 times” means 1 * 2^3 = 1 * 2 * 2 * 2 = 8
“Start with 3 and double 3 times” means 3 * 2^3 = 3 * 2 * 2 * 2 = 24

Whenever you see an plain exponent by itself (like 2^3), we’re starting with 1.0.

Understanding the Exponential Scaling Factor

When multiplying, we can just state the final scaling factor. Want it 8 times larger? Multiply by 8. Done.

Exponents are a bit… finicky:

You: I’d like to grow this number.

Expand-o-tron: Ok, stick it in.

You: How big will it get?

Expand-o-tron: Gee, I dunno. Let’s find out…

You: Find out? I was hoping you’d kn-

Expand-o-tron: Shh!!! It’s growing! It’s growing!

You: …

Expand-o-tron: It’s done! My masterpiece is alive!

You: Can I go now?

The expand-o-tron is indirect. Just looking at it, you’re not sure what it’ll do: What does 3^10 mean to you? How does it make you feel? Instead of a nice tidy scaling factor, exponents want us to feel, relive, even smell the growing process. Whatever you end with is your scaling factor.

It sounds roundabout and annoying. You know why? Most things in nature don’t know where they’ll end up!

Do you think bacteria plans on doubling every 14 hours? No — it just eats the moldy bread you forgot about in the fridge as fast as it can, and as it gets more it starts growing even faster. To predict the behavior, we use how fast they’re growing (current rate) and how long they’ll be changing (time) to figure out their final value.

The answer has to be worked out — exponents are a way of saying “Begin with these conditions, start changing, and see where you end up”. The expand-o-tron (or our calculator) does the work by crunching the numbers to get the final scaling factor. But someone has to do it.

Understanding Fractional Powers

Let’s see if the expand-o-tron can help us understand exponents. First up: what does at 2^1.5 mean?

It’s confusing when we think of repeated multiplication. But the expand-o-tron makes it simple: 1.5 is just the amount of time in the machine.

2^1 means 1 second in the machine (2x growth)
2^2 means 2 seconds in the machine (4x growth)

2^1.5 means 1.5 seconds in the machine, so somewhere between 2x and 4x growth (more later). The idea of “repeated counting” had us stuck using whole numbers, but fractional seconds are completely fine.

Multiplying exponents

What if we want to two growth cycles back-to-back? Let’s say we use the machine for 2 seconds, and then use it for 3 seconds at the exact same power:

$\displaystyle{x^2 \cdot x^3 = ?}$

Think about your regular microwave — isn’t this the same as one continuous cycle of 5 seconds? It sure is. As long as the power setting (base) stayed the same, we can just add the time:

$\displaystyle{x^y \cdot x^z = x^{y + z}}$

Again, the expand-o-tron gives us a scaling factor to change our number. To get the total effect from two consecutive uses, we just multiply the scaling factors together.

Square roots

Let’s keep going. Let’s say we’re at power level a and grow for 3 seconds:

$\displaystyle{a^3}$

Not too bad. Now what would growing for half that time look like? It’d be 1.5 seconds:

$\displaystyle{a^{1.5}}$

Now what would happen if we did that twice?

$\displaystyle{a^{1.5} \cdot a^{1.5} = a^3}$

$\displaystyle{\text{partial growth} \cdot \text{partial growth} = \text{full growth}}$

Looking at this equation, we see “partial growth” is the square root of full growth! If we divide the time in half we get the square root scaling factor. And if we divide the time in thirds?

$\displaystyle{a^1 \cdot a^1 \cdot a^1 = a^3}$

$\displaystyle{\text{partial growth} \cdot \text{partial growth} \cdot \text{partial growth} = \text{full growth}}$

And we get the cube root! For me, this is an intuitive reason why dividing the exponents gives roots: we split the time into equal amounts, so each “partial growth” period must have the same effect. If three identical effects are multiplied together, it means they’re each a cube root.

Negative exponents

Now we’re on a roll — what does a negative exponent mean? Negative seconds means going back in time! If going forward grows by a scaling factor, going backwards should shrink by it.

$\displaystyle{2^{-1} = \frac{1}{2^1}}$

The sentence means “1 second ago, we were at half our current amount (1/2^1)”. In fact, this is a neat part of any exponential graph, like 2^x:

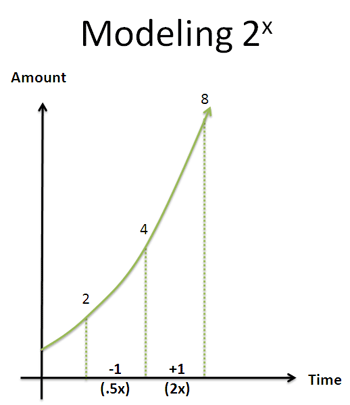
Pick a point like 3.5 seconds (2^3.5 = 11.3). One second in the future we’ll be at double our current amount (2^4.5 = 22.5). One second ago we were at half our amount (2^2.5 = 5.65).

This works for any number! Wherever 1 million is, we were at 500,000 one second before it. Try it below:

Taking the zeroth power

Now let’s try the tricky stuff: what does 3^0 mean? Well, we set the machine for 3x growth, and use it for… zero seconds. Zero seconds means we don’t even use the machine!

Our new and old values are the same (new = old), so the scaling factor is 1. Using 0 as the time (power) means there’s no change at all. The scaling factor is always 1.

Taking zero as a base

How do we interpret 0^x? Well, our growth amount is “0x” — after a second, the expand-o-tron obliterates the number and turns it to zero. But if we’ve obliterated the number after 1 second, it really means any amount of time will destroy the number:

0^(1/n) = nth root of 0^1 = nth root of 0 = 0

No matter the tiny power we raise it to, it will be some root of 0.

Zero to the zeroth power

At last, the dreaded 0^0. What does it mean?

The expand-o-tron to the rescue: 0^0 means a 0x growth for 0 seconds!

Although we planned on obliterating the number, we never used the machine. No usage means new = old, and the scaling factor is 1. 0^0 = 1 * 0^0 = 1 * 1 = 1 — it doesn’t change our original number. Mystery solved!

(For the math geeks: Defining 0^0 as 1 makes many theorems work smoothly. In reality, 0^0 depends on the scenario (continuous or discrete) and is under debate. The microwave analogy isn’t about rigor — it helps me see why it could be 1, in a way that “repeated counting” does not.)

Here's what happens when we try to plug in actual numbers:

Advanced: Repeated Exponents (a to the b to the c)

Repeated exponents are tricky. What does

$\displaystyle{\Large (2^a)^b}$

mean? It’s “repeated multiplication, repeated” — another way of saying “do that exponent thing once, and do it again”. Let’s dissect it:

$\displaystyle{(2^3)^4}$

First, I want to grow by doubling each second: do that for 3 seconds (2^3)
Then, whatever my number is (8x), I want to grow by that new amount for 4 seconds (8^4)

The first exponent (^3) just knows to take “2″ and grow it by itself 3 times. The next exponent (^4) just knows to take the previous amount (8) and grow it by itself 4 times. Each time unit in “Phase II” is the same as repeating all of Phase I:

$\displaystyle{(2^3)^4 = 2^3 \cdot 2^3 \cdot 2^3 \cdot 2^3 = 2^{3+3+3+3} = 2^{12} }$

This is where the repeated counting interpretation helps get our bearings. But then we bring out the expand-o-tron: we grow for 3 seconds in Phase I, and redo that for 4 more seconds. It works for fractional powers — for example,

$\displaystyle{(2^{3.1})^{4.2}}$

means “Grow for 3.1 seconds, and use that new growth rate for 4.2 seconds”. We can smush together the time (3.1 × 4.2) like this:

$\displaystyle{(a^b)^c = a^{b\cdot c} = (a^c)^b}$

It’s different, so try some examples:

(2^1)^x means “Grow at 2 for 1 second, and ‘do that growth’ for x more seconds”.
7 = (7^0.5)^2 means “We can jump to 7 all at once. Or, we can plan on growing to 7 but only use half the time ($\sqrt{7}$). But we can do that process for 2 seconds, which gives us the full amount ($\sqrt{7}^2 = 7$).”

We’re like kids learning that 3 times 7 = 7 times 3. (Or that a% of b = b% of a — it’s true!).

Advanced: Rewriting Exponents For The Grower

The expand-o-tron is a bit strange: numbers start growing the instant they’re inside, but we specify the desired growth at the end of each second.

We say we want 2x growth at the end of the first second. But how do we know what rate to start off with? How fast should we be growing at 0.5 seconds? It can’t be the full amount, or else we’ll overshoot our goal as our interest compounds.

Here’s the key: Growth curves written like 2^x are from the observer’s viewpoint, not the grower.

The value “2″ is measured at the end of the interval and we work backwards to create the exponent. This is convenient for us, but not the growing quantity — bacteria, radioactive elements and money don’t care about lining up with our ending intervals!

No, these critters know their current, instantaneous growth rate, and don’t try to line it up with our boundaries. It’s just like understanding radians vs. degrees — radians are “natural” because they are measured from the mover’s viewpoint.

To get into the grower’s viewpoint, we use the magical number e. There’s much more to say, but we can convert any “observer-focused” formula like 2^x into a “grower-focused” one:

$\displaystyle{2^x = (e^{\ln(2)})^x = e^{\ln(2)x} }$

In this case, ln(2) = .693 = 69.3% is the instantaneous growth rate needed to look like 2^x to an observer. When you enter “2x growth at the end of each period”, the expand-o-tron knows to grow the number at a rate of 69.3%.

We’ll save these details for another day — just remember the difference between the grower’s instantaneous growth rate (which the bacteria controls) and the observer’s chart that’s measured at the end of each interval. Underneath it all, every exponential curve is a scaled version of e^x:

$\displaystyle{a^x = (e^{\ln(a)})^x = e^{\ln(a)x} }$

Every exponent is a variation of e, just like every number is a scaled version of 1.

Why use this analogy?

Does the expand-o-tron exist? Do numbers really gather up in a line? Nope — they’re ways of looking at the world.

The expand-o-tron removes the mental hiccups when seeing 2^1.5 or even 0^0: it’s just 0x growth for 0 seconds, which doesn’t change the number. Everything from slide rules to Euler’s formula begins to click once we recognize the core theme of growth — even beasts like i^i can be tamed.

Friends don’t let friends think of exponents as repeated multiplication. Happy math.