How To Think With Exponents And Logarithms

Here’s a trick for thinking through problems involving exponents and logs. Just ask two questions:

1) Are we talking about inputs (cause of the change) or outputs (the actual change that happened?)

Logarithms reveal the inputs that caused the growth
Exponents find the final result of growth

2) Are we talking about the grower’s perspective, or an observer’s?

e and the natural log are from the grower’s instant-by-instant perspective
Base 10, Base 2, etc. are measurements convenient for a human observer

In my head, I put the options in a table:

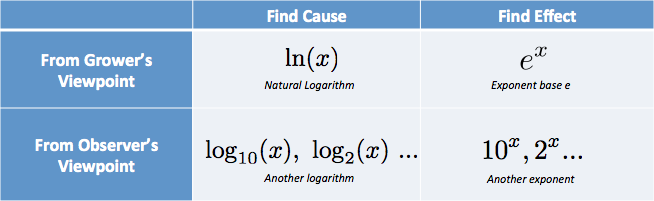
I have thoughts like “I need the cause, from the grower’s perspective… that’s the natural log.”. (Natural log is abbreviated with lowercase LN, from the high-falutin’ logarithmus naturalis.)

I was frustrated with classes that described the inner part of the table, the raw functions, without the captions that explained when to use them!

That won’t fly, let’s get direct practice thinking with logs and exponents.

Scenario: Describing GDP Growth

Here’s a typical example of growth:

From 2000 to 2010, the US GDP changed from 9.9 trillion to 14.4 trillion

Ok, sure, those numbers show change happened. But we probably want insight into the cause: What average annual growth rate would account for this change?

Immediately, my brain thinks “logarithms” because we’re working backwards from the growth to the rate that caused it. I start with a thought like this:

$\displaystyle{\text{logarithm of change} \rightarrow \text{cause of growth} }$

A good start, but let’s sharpen it up.

First, which logarithm should we use?

By default, I pick the natural logarithm. Most events end up being in terms of the grower (not observer), and I like “riding along” with the growing element to visualize what’s happening. (Radians are similar: they measure angles in terms of the mover.)

Next question: what change do we apply the logarithm to?

We’re really just interested in the ratio between start and finish: 9.9 trillion to 14.4 trillion in 10 years. This is the same growth rate as going from \$9.90 to \$14.40 in the same period.

We can sharpen our thought:

$\displaystyle{\text{natural logarithm of growth ratio} \rightarrow \text{cause of growth} }$

$\displaystyle{\ln(\frac{14.4}{9.9}) = .374}$

Ok, the cause was a rate of .374 or 37.4%. Are we done?

Not yet. Logarithms don’t know about how long a change took (we didn’t plug in 10 years, right?). They give us a rate as if all the change happened in a single time period.

The change could indeed be a single year of 37.4% continuous growth, or 2 years of 18.7% growth, or some other combination.

From the scenario, we know the change took 10 years, so the rate must have been:

$\displaystyle{ \text{rate} = \frac{.374}{10} = .0374 = 3.74\%}$

From the viewpoint of instant, continuous growth, the US economy grew by 3.74% per year.

Are we done now? Not quite!

This continuous rate is from the grower’s perspective, as if we’re “riding along” with the economy as it changes. A banker probably cares about the human-friendly, year-over-year difference. We can figure this out by letting the continuous growth run for a year:

$\displaystyle{\text{exponent with rate and time} \rightarrow \text{effect of growth} }$

$\displaystyle{e^{\text{rate} \cdot \text{time}} = \text{growth}}$

$\displaystyle{e^{.0374 \cdot 1} = 1.0381}$

The year-over-year gain is 3.8%, slightly higher than the 3.74% instantaneous rate due to compounding. Here’s another way to put it:

From an instant-by-instant basis, a given part of the economy is growing by 3.74%, modeled by $e^(.0374 * years)$
On a year-by-year basis, with compounding effects worked out, the economy grows by 3.81%, modeled by $1.0381^years$

In finance, we may want the year-over-year change which can be compared nicely with other trends. In science and engineering, we prefer modeling behavior on an instantaneous basis.

Scenario: Describing Natural Growth

I detest contrived examples like “Assume bacteria doubles every 24 hours, find its growth formula.”. Do bacteria colonies replicate on clean human intervals, and do we wait around for an exact doubling?

A better scenario: “Hey, I found some bacteria, waited an hour, and the lump grew from 2.3 grams to 2.32 grams. I’m going to lunch now. Figure out how much we’ll have when I’m back in 3 hours.”

Let’s model this. We’ll need a logarithm to find the growth rate, and then an exponent to project that growth forward. Like before, let’s keep everything in terms of the natural log to start.

The growth factor is:

$\displaystyle{\text{logarithm of change} \rightarrow \text{cause of growth} }$

$\displaystyle{\ln(\text{growth}) = \ln(2.32/2.3) = .0086 = .86\%}$

That’s the rate for one hour, and the general model to project forward will be

$\displaystyle{\text{exponent with rate and time} \rightarrow \text{effect of growth} }$

$\displaystyle{e^{.0086 \cdot \text{hours}} \rightarrow \text{effect of growth} }$

If we start with 2.32 and grow for 3 hours we’ll have:

$\displaystyle{2.32 \cdot e^{.0086 \cdot 3} = 2.38}$

Just for fun, how long until the bacteria doubles? Imagine waiting for 1 to turn to 2:

$\displaystyle{1 \cdot e^{.0086 \cdot \text{hours}} = 2}$

We can mechanically take the natural log of both sides to “undo the exponent”, but let’s think intuitively.

If 2 is the final result, then ln(2) is the growth input that got us there (some rate × time). We know the rate was .0086, so the time to get to 2 would be:

$\displaystyle{ \text{hours} = \frac{\ln(2)}{\text{rate}} = \frac{.693}{.0086} = 80.58}$

The colony will double after ~80 hours. (Glad you didn’t stick around?)

What Does The Perspective Change Really Mean?

Figuring out whether you want the input (cause of growth) or output (result of growth) is pretty straightforward. But how do you visualize the grower’s perspective?

Imagine we have little workers who are building the final growth pattern (see the article on exponents):

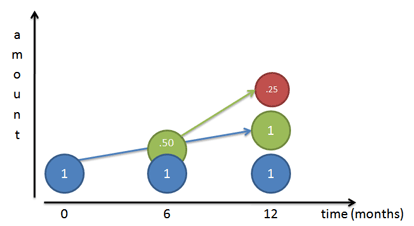
$compound interest$

If our growth rate is 100%, we’re telling our initial worker (Mr. Blue) to work steadily and create a 100% copy of himself by the end of the year. If we follow him day-by-day, we see he does finish a 100% copy of himself (Mr. Green) at the end of the year.

But… that worker he was building (Mr. Green) starts working as well. If Mr. Green first appears at the 6-month mark, he has a half-year to work (same annual rate as Mr. Blue) and he builds Mr. Red. Of course, Mr. Red ends up being half done, since Mr. Green only has 6 months.

What if Mr. Green showed up after 4 months? A month? A day? A second? If workers begin growing immediately, we get the instant-by-instant curve defined by $e^x$:

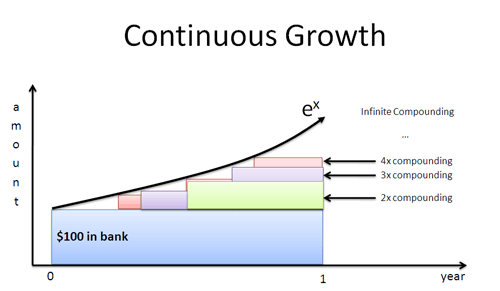
The natural log gives a growth rate in terms of an individual worker’s perspective. We plug that rate into $e^x$ to find the final result, with all compounding included.

Using Other Bases

Switching to another type of logarithm (base 10, base 2, etc.) means we’re looking for some pattern in the overall growth, not what the individual worker is doing.

Each logarithm asks a question when seeing a change:

Log base e: What was the instantaneous rate followed by each worker?
Log base 2: How many doublings were required?
Log base 10: How many 10x-ings were required?

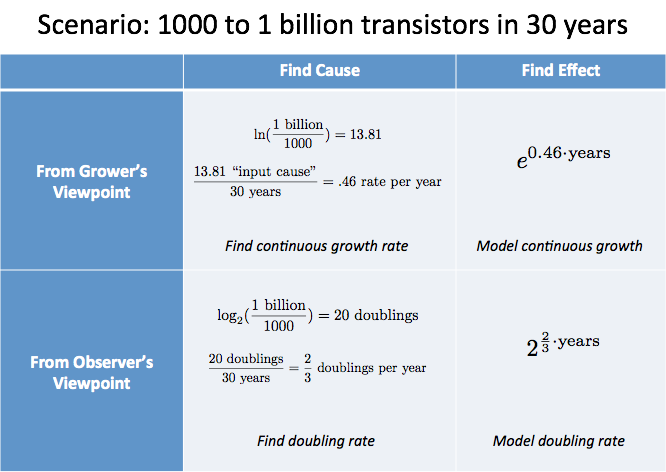
Here’s a scenario to analyze:

Over 30 years, the transistor counts on typical chips went from 1000 to 1 billion

How would you analyze this?

Microchips aren’t a single entity that grow smoothly over time. They’re separate editions, from competing companies, and indicate a general tech trend.
Since we’re not “riding along” with an expanding microchip, let’s use a scale made for human convenience. Doubling is easier to think about than 10x-ing.

With these assumptions we get:

$\displaystyle{\text{logarithm of change} \rightarrow \text{cause of growth} }$

$\displaystyle{\log_2(\frac{\text{1 billion}}{1000}) = \log_2(\text{1 million}) \sim \text{20 doublings}}$

The “cause of growth” was 20 doublings, which we know occurred over 30 years. This averages 2/3 doublings per year, or 1.5 years per doubling — a nice rule of thumb.

From the grower’s perspective, we’d compute $\ln(\text{1 billion}/1000) / \text{30 years} = 46\%$ continuous growth (a bit harder to relate to in this scenario).

We can summarize our analysis in a table:

Summary

Learning is about finding the hidden captions behind a concept. When is it used? What point view does it bring to the problem?

My current interpretation is that exponents ask about cause vs. effect and grower vs. observer. But we’re never done; part of the fun is seeing how we can recaption old concepts.

Happy math.

Appendix: The Change Of Base Formula

Here’s how to think about switching bases. Assuming a 100% continuous growth rate,

ln(x) is the time to grow to x
ln(2) is the time to grow to 2

Since we have the time to double, we can see how many would “fit” in the total time to grow to x:

$\displaystyle{\text{number of doublings from 1 to x} = \frac{\ln(x)}{\ln(2)} = \log_2(x)}$

For example, how many doublings occur from 1 to 64?

Well, ln(64) = 4.158. And ln(2) = .693. The number of doublings that fit is:

$\displaystyle{\frac{\ln(64)}{\ln(2)} = \frac{4.158}{.693} = 6}$

In the real world, calculators may lose precision, so use a direct log base 2 function if possible. And of course, we can have a fractional number: Getting from 1 to the square root of 2 is “half” a doubling, or log₂(1.414) = 0.5.

Changing to log base 10 means we’re counting the number of 10x-ings that fit:

$\displaystyle{\text{number of 10x-ings from 1 to x} = \frac{\ln(x)}{\ln(10)} = \log_{10}(x) }$

Neat, right? Read Using Logarithms in the Real World for more examples.

How To Think With Exponents And Logarithms

Scenario: Describing GDP Growth

Scenario: Describing Natural Growth

What Does The Perspective Change Really Mean?

Using Other Bases

Summary

Appendix: The Change Of Base Formula

Other Posts In This Series

Join 450k Monthly Readers