Surprising Patterns in the Square Numbers (1, 4, 9, 16…)

A quick puzzle for you — look at the first few square numbers:

1, 4, 9, 16, 25, 36, 49…

And now find the difference between consecutive squares:

1 to 4   = 3
4 to 9   = 5
9 to 16  = 7
16 to 25 = 9
25 to 36 = 11
…

Huh? The odd numbers are sandwiched between the squares?

Strange, but true. Take some time to figure out why — even better, find a reason that would work on a nine-year-old. Go on, I’ll be here.

Exploring Patterns

We can explain this pattern in a few ways. But the goal is to find a convincing explanation, where we slap our forehands with “ah, that’s why!”. Let’s jump into three explanations, starting with the most intuitive, and see how they help explain the others.

Geometer’s Delight

It’s easy to forget that square numbers are, well… square! Try drawing them with pebbles

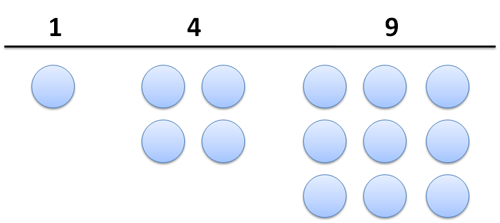
Notice anything? How do we get from one square number to the next? Well, we pull out each side (right and bottom) and fill in the corner:

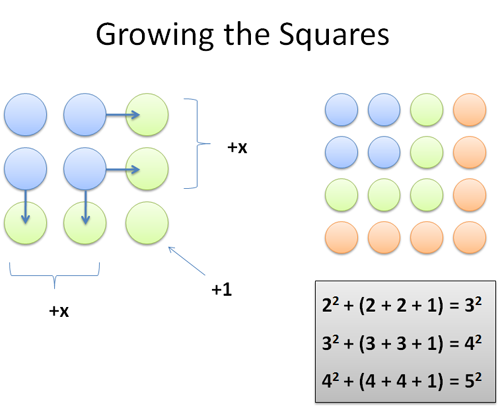
While at 4 (2×2), we can jump to 9 (3×3) with an extension: we add 2 (right) + 2 (bottom) + 1 (corner) = 5. And yep, 2×2 + 5 = 3×3. And when we’re at 3, we get to the next square by pulling out the sides and filling in the corner: Indeed, 3×3 + 3 + 3 + 1 = 16.

Each time, the change is 2 more than before, since we have another side in each direction (right and bottom).

Another neat property: the jump to the next square is always odd since we change by “2n + 1″ (2n must be even, so 2n + 1 is odd). Because the change is odd, it means the squares must cycle even, odd, even, odd…

And wait! That makes sense because the integers themselves cycle even, odd, even odd… after all, a square keeps the “evenness” of the root number (even * even = even, odd * odd = odd).

Funny how much insight is hiding inside a simple pattern. (I call this technique “geometry” but that’s probably not correct — it’s just visualizing numbers).

An Algebraist’s Epiphany

Drawing squares with pebbles? What is this, ancient Greece? No, the modern student might argue this:

We have two consecutive numbers, n and (n+1)
Their squares are n² and (n+1)²
The difference is (n+1)² – n² = (n²+ 2n + 1) – n² = 2n + 1

For example, if n=2, then n²=4. And the difference to the next square is thus (2n + 1) = 5.

Indeed, we found the same geometric formula. But is an algebraic manipulation satisfying? To me, it’s a bit sterile and doesn’t have that same “aha!” forehead slap. But, it’s another tool, and when we combine it with the geometry the insight gets deeper.

Calculus Madness

Calculus students may think: “Dear fellows, we’re examining the curious sequence of the squares, f(x) = x^2. The derivative shall reveal the difference between successive elements”.

And deriving f(x) = x^2 we get:

$\displaystyle{\frac{d}{dx}x^{2}=2x}$

Close, but not quite! Where is the missing +1?

Let’s step back. Calculus explores smooth, continuous changes — not the “jumpy” sequence we’ve taken from 2² to 3² (how’d we skip from 2 to 3 without visiting 2.5 or 2.00001 first?).

But don’t lose hope. Calculus has algebraic roots, and the +1 is hidden. Let’s dust off the definition of the derivative:

$\displaystyle{f'(x)=\lim_{dx\to 0}{f(x+dx)-f(x)\over dx}}$

Forget about the limits for now — focus on what it means (the feeling, the love, the connection!). The derivative is telling us “compare the before and after, and divide by the change you put in”. If we compare the “before and after” for f(x) = x^2, and call our change “dx” we get:

$\displaystyle{\frac{(x+dx)^2 - x^2}{dx} = \frac{(x^2+2x \cdot dx + dx^2) - x^2}{dx} = \frac{2x \cdot dx + dx^2}{dx}}$

$\displaystyle{= 2x + dx}$

Now we’re getting somewhere. The derivative is deep, but focus on the big picture — it’s telling us the “bang for the buck” when we change our position from “x” to “x + dx”. For each unit of “dx” we go, our result will change by 2x + dx.

For example, if we pick a “dx” of 1 (like moving from 3 to 4), the derivative says “Ok, for every unit you go, the output changes by 2x + dx (2x + 1, in this case), where x is your original starting position and dx is the total amount you moved”. Let’s try it out:

Going from 3² to 4² would mean:

x = 3, dx = 1
change per unit input: 2x + dx = 6 + 1 = 7
amount of change: dx = 1
expected change: 7 * 1 = 7
actual change: 4² – 3² = 16 – 9 = 7

We predicted a change of 7, and got a change of 7 — it worked! And we can change “dx” as much as we like. Let’s jump from 3² to 5²:

x = 3, dx = 2
change per unit input: 2x + dx = 6 + 2 = 8
number of changes: dx = 2
total expected change: 8 * 2 = 16
actual change: 5² – 3² = 25 – 9 = 16

Whoa! The equation worked (I was surprised too). Not only can we jump a boring “+1″ from 3² to 4², we could even go from 3² to 10² if we wanted!

Sure, we could have figured that out with algebra — but with our calculus hat, we started thinking about arbitrary amounts of change, not just +1. We took our rate and scaled it out, just like distance = rate * time (going 50mph doesn’t mean you can only travel for 1 hour, right? Why should 2x + dx only apply for one interval?).

My pedant-o-meter is buzzing, so remember the giant caveat: Calculus is about the micro scale. The derivative “wants” us to explore changes that happen over tiny intervals (we went from 3 to 4 without visiting 3.000000001 first!). But don’t be bullied — we got the idea of exploring an arbitrary interval “dx”, and dagnabbit, we ran with it. We’ll save tiny increments for another day.

Lessons Learned

Exploring the squares gave me several insights:

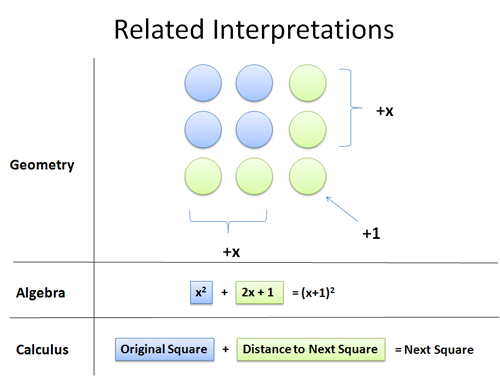
Seemingly simple patterns (1, 4, 9, 16…) can be examined with several tools, to get new insights for each. I had completely forgotten that the ideas behind calculus (x going to x + dx) could help investigate discrete sequences.
It’s all too easy to sandbox a mathematical tool, like geometry, and think it can’t shed light into higher levels (the geometric pictures really help the algebra, especially the +1, pop). Even with calculus, we’re used to relegating it to tiny changes — why not let dx stay large?
Analogies work on multiple levels. It’s clear that the squares and the odds are intertwined — starting with one set, you can figure out the other. Calculus expands this relationship, letting us jump back and forth between the integral and derivative.

As we learn new techniques, don’t forget to apply them to the lessons of old. Happy math.

Appendix: The Cubes!

I can’t help myself: we studied the squares, now how about the cubes?

1, 8, 27, 64…

How do they change? Imagine growing a cube (made of pebbles!) to a larger and larger size — how does the volume change?