Rethinking Arithmetic: A Visual Guide

Arithmetic gives us tools to smoosh, slide and stretch numbers. These transformations are handy: sometimes there’s things in the real world we want to smoosh, slide and stretch in the same way.

Why’s this important?

Seeing arithmetic as a type of transformation prepares you to make sense of seemingly-weird concepts, like the square root of -1, and visualize problems in a new way. Let’s take a look.

Addition

Addition is simple, yet it can mean several things:

Accumulate: Count up similar quantities (often for tangible items).
Slide: Shifting a number along a scale (for less tangible things, like temperature).
Combine: Make a new quantity out of two different ones (like notes in a music chord).

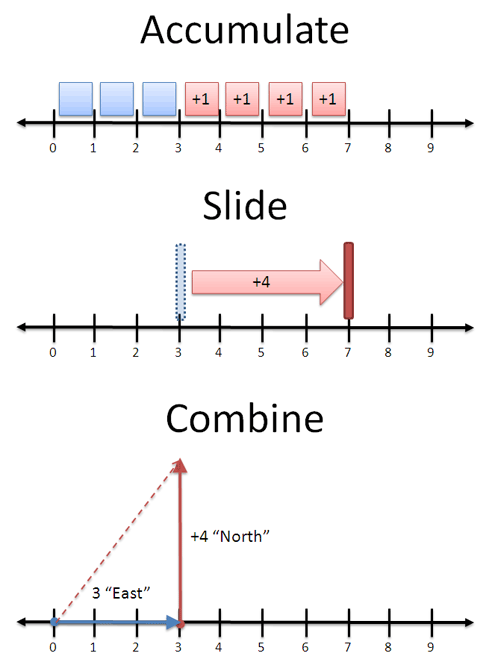
What’s the right meaning? It depends on the context. When adding apples, we count up similar items (3 apples + 4 apples = 7 apples). When measuring temperature, we add heat to move along a scale (3 degrees + 4 degrees = 7 degrees).

When adding vectors, a combination makes the most sense: 3 blocks east + 4 blocks north = 5 blocks in a new direction (“as the crow flies” distance). In this case, you must track the component parts, keeping “North” and “East” separate. When adding apples, you can combine everything: once you have 7, you don’t care that it was once 3 and 4.

A single operation (addition) can take on several intuitive meanings. This list isn’t exhaustive — they are the interactions I’ve noticed, and I’m sure you have others.

Multiplication

Multiplication can also be interpreted in several ways:

Repetition: Performing multiple additions.
Scaling: Making a number grow or shrink all at once.

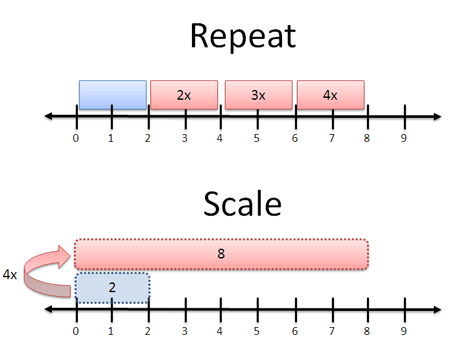
Context determines our meaning. With apples, “4x” means turning an order of 2 apples into an order of 8 (4 groups of 2). With photo software, “4x” means expanding a 2-inch photo to be 8 inches long. Each meaning is different: you’d be annoyed if I gave you a giant, 5-lb apple or 4 separate photos.

In a narrow sense, multiplication is “repeated addition”. Sure. But that’s not always the easiest interpretation — care to “repeatedly add” 7.3 times?

Negatives and Inverses

Negatives and inverses both represent the idea of “reverse” or “opposite”. But that’s ambiguous: What’s the opposite of multiplying by two?

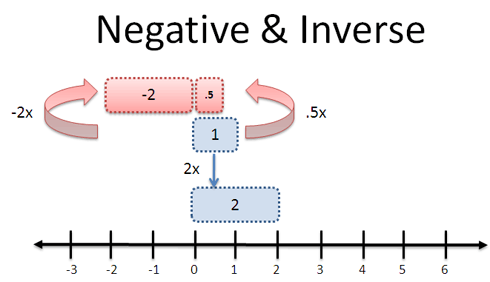
“Opposite” can mean a few things:

Multiply by 1/2: Turn a profit of 1 into a profit of 1/2 (“unscale” it)
Multiply by -2: Turn a profit of 1 into a loss of 2 (flip it)

Yet again, our context determines meaning. When a company “reverses a gain” it implies a loss, aka multiplying by a negative. When we “reverse a zoom” in photo software, we want to shrink the photo (not mirror-image it), so we multiply by 1/2. Context, context, context (tired of that word yet?).

When adding, there’s only one type of opposite: the reverse of +8 is -8. But the trick is to know that -8 really means “0-8″ or even “0 + (-8)”: you’re moving backwards relative to some reference point. Moving “in reverse” means different things depending if your original direction was East or North.

What’s in an equation?

Equations ask questions. When you see

$\displaystyle{x^2 = 9}$

It’s more than just a plug and chug problem. Think about the question like this:

$\displaystyle{1 * x^2 = 9}$

What transformation (“times x”), when applied twice, will turn 1 into 9?

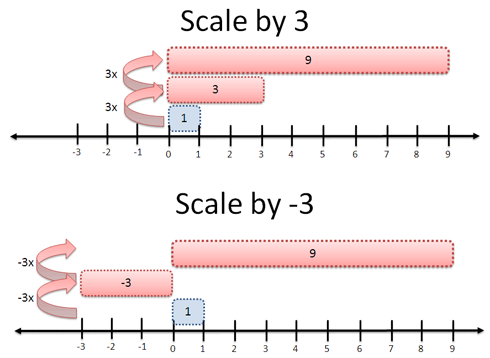
We have two answers:

Scale by 3 (times 3): Do it twice and you’ll get 9: 1 * 3 * 3 = 9
Scale by 3 and flip (times -3): Done twice, you get 9 also: 1 * -3 * -3 = 9

Nifty. I included “1″ to show what is being transformed. Sure, it’s optional, but it’s not something we think about. What is the “times 3″ acting on?

Stepping back this way, we can see arithmetic as a method to push, pull, tug and squeeze one number into another. We’ve managed to turn one large transformation (“times 9″) into two equal, smaller ones (“times -3″ or “times 3″).

Real-World Example: Random Numbers

Enough theory — let’s show this mindset in action. Most programming languages offer a random() function that gives a number from 0 to 1. But what if you want something from 5-10?

The question is: how do I transform my range of 0-1 into a range from 5-10?

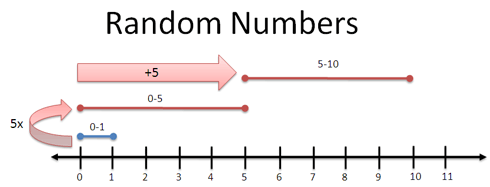
Arithmetic to the rescue!

First, you stretch 0-1 into 0-5 by multiplying by 5
Next, slide 0-5 to 5-10 by adding 5
And tada. You have a range from 5-10.

Try it out below. You start with a number “r” and transform it into the proper range.

By the way, this range could be the ages 18-65, the years 1960-2007, or the temperatures 30F – 80F for use in your simulation (everyone runs simulations, right?). No matter your range, you can start with the “0 to 1″ building block and modify it.

Sure, you can figure this out without a diagram, but sometimes it’s nice to visualize what’s happening. Our brain is a vision-processing supercomputer, so let’s use its strengths.

What’s next?

This post introduces the idea that arithmetic is a transformation. You bend numbers into other ones, and each transformation has a meaning. Some fit a situation better than others: use the one you like most.

The goal isn’t to turn multiplication into a cumbersome diagramming process. It’s a technique, a mindset, a new weapon to use against seemingly complex operations.

When studying linear algebra (matrices), you can view multiplication as a type of transformation (scaling, rotating, skewing), instead of a bunch of operations that change a matrix around. This approach will help when we cover imaginary numbers, that foul beast which has befuddled many students.

Little insights help bigger ideas click. Happy math.