Learning How to Count (Avoiding The Fencepost Problem)

Counting isn't easy. Suppose your boss wants you to work from 8am to 11am, and mop floors 8 to 11. Simple - it's one floor per hour, right?

Nope! There are 4 floors to mop (8, 9, 10 and 11) but only 3 hours to work (8-9, 9-10, and 10-11).

Whoa -- we count floors and hours differently? You bet. And somehow, if the boss said "Mop floors 8 to 11 on April 8th to 11th" everything would be ok.

Today let's unravel this counting mystery.

Basic Counting

Numbers help us know "how many". Take a numbered list of houses:

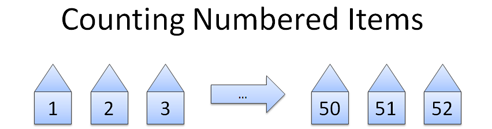
There's 52 houses there. Don't count each one: the addresses count for us! The numbers label the houses one by one, just as we'd do. We can just read the last item: "1 to 52" is 52 houses.

Examples:

Employee ID cards from 1 to 3493. There are 3493 employees.
Days of the month from 1 to 31. There are 31 days in that month.

What Does Subtraction Mean?

We often see numbers as points on a line:

These points can be houses, floors, or plain integers. Whatever they are, they're labeled so we can count them easily. 1 to 10 means ten items.

But what about a range like 8 to 11? How many items are there?

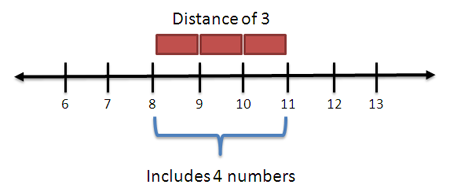
We'd probably try subtraction: 11 - 8 = 3, right? But here's the key:

Subtraction is a span between numbers, not a count

The equation 11 - 8 = 3 means there are 3 "spans" between 8 and 11, but four numbers in that range!

A span is a distance measure, like time from 8am and 11am (3 hours) or the distance between 8 and 11 inches (3 inches).

But when counting floors, we aren't asking for the distance between floors 8 to 11 (which is in fact 3 floors or 30 feet, assuming 10 feet per floor). We want a count of how many items the range "8 to 11" includes!

Working With Spans and Counts

Realizing there are two types of counting was a big mental shift. We have two possible choices when "counting" from a to b:

Distance from a to b: b - a [regular subtraction]
Number of items from a to b: b - a + 1 (span touches extra element)

Ok, the formulas work. But why does a count need an extra element?

Well, the shortest span (distance 1) actually touches two numbers:

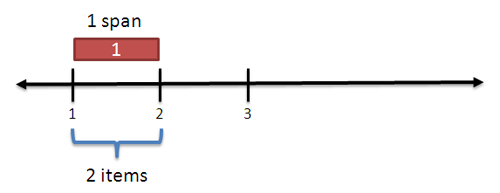
A span is a line segment with a start and end; a span of distance 1 covers 2 points. As we grow the span, we gobble up more points and are always "one ahead".

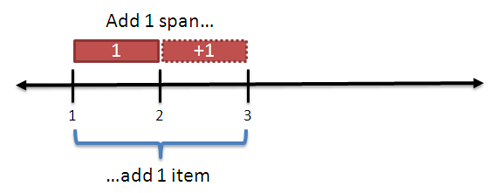
Here's another way to think about it. A span of 3 means we start with an item (#8) and count out 3 more (#9, #10, #11). So, a span of N includes 1 original item and N new items, for a total of N + 1 items.

I like seeing new viewpoints; use what works for you.

The Fencepost Problem

The confusion between spans and counts is commonly called the fencepost problem. Are you counting the posts (points) or the distance between them (fence spans)?

The question goes like this:

You're building a fence 100 feet long, with posts every 10 feet. How many posts do you need?

Here's how to think about it with our new mental model:

Hrm, we want a fence 100 feet long. Ok: that's a span of ten, 10-foot segments. But we want the number of posts: how many posts do those ten segments touch? Well, a span always touches an extra point, so ten segments means 11 posts.

11 fenceposts it is. But the problem isn't natural for me - I have to think about spans vs points. I'd double-check with a smaller example - a fence that is 10 feet long needs 2 posts, so yes, we need an "extra post".

A few more examples:

Working Days: I worked April 8th to April 11th. How many days did I work? Well, that's a span of 3 (11-8), but we "touch" 4 days: April 8, 9, 10, 11. So I worked 4 days.
Hours: Hours are like spans. Working from 8 to 11 means you are covering the spans 8-9, 9-10, and 10-11. 8 to 11 means a "timespan" of 3 hours.
Seconds: I start a race, and the start time at 12:01:08 (12 hours, 1 minute, 8 seconds). It ends at 12:01:11. How long did it go? 11 - 8 = 3 seconds. (Short race)

Interesting, eh? Some units of time are measured with spans (hours, seconds) and others are items to be counted (days).

The measuring type depends on the context. We see shorter units of time as "instants" and want the duration between those instants, not the "number" of instants we touched.

We see days as a large fuzzy blob covering a time period (9am-5am) -- and we want to know how many blobs we covered. Saying you worked April 8 to April 9th implies you worked a timespan of 9am-5pm on two days.

The counting type depends on the context - but at least you know why we count them differently.

Final Thoughts

Counting isn't simple. The fencepost problem and other "off by one" boundary errors are notoriously common. But don't just remember a special trick, like "sometimes I need to add 1". Remember there are two ways to measure something:

Are we measuring a difference (distance, time)? Then do regular subtraction to get a span.
Are we counting items? Then subtract and add 1 (b - a + 1) - we want the number of items the span touches.

It's not easy to recognize the difference - we're used to having one way to measure. Try a simple example (a fence 10 feet long) to test if you've got a count or span.

I've run into the fencepost problem many times, but the articles I read just told me how to fix it. No, no, no - why does it happen?

It turns out we often use the same approach for two different types of counting. And while the right method may not be obvious, at least we know to try both approaches. Happy math.