Demystifying the Natural Logarithm (ln)

After understanding the exponential function our next target is the natural logarithm.

Given how the natural log is described in math books, there’s little “natural” about it: it’s defined as the inverse of e^x, a strange enough exponent already.

But there’s a fresh, intuitive explanation: The natural log gives you the time needed to reach a certain level of growth.

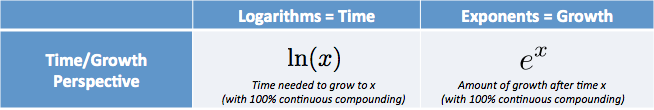
Suppose you have an investment in gummy bears (who doesn’t?) with an interest rate of 100% per year, growing continuously. If you want 10x growth, assuming continuous compounding, you’d wait only ln(10) or 2.302 years. Don’t see why it only takes a few years to get 10x growth? Read more about e.

e and the Natural Log are twins:

e^x is the amount of continuous growth after a certain amount of time.
Natural Log (ln) is the amount of time needed to reach a certain level of continuous growth

Not too bad, right? While the mathematicians scramble to give you the long, technical explanation, let’s dive into the intuitive one.

E is about growth

The number e is about continuous growth. As we saw last time, e^x lets us merge rate and time: 3 years at 100% growth is the same as 1 year at 300% growth, when continuously compounded.

We can take any combination of rate and time (50% for 4 years) and convert the rate to 100% for convenience (giving us 100% for 2 years). By converting to a rate of 100%, we only have time to think about:

$\displaystyle{e^x = e^{rate \cdot time} = e^{1.0 \cdot time} = e^{time}}$

Intuitively, e^x means:

How much growth do I get after after x units of time (and 100% continuous growth)
For example: after 3 time periods I have e^3 = 20.08 times the amount of “stuff”.

e^x is a scaling factor, showing us how much growth we’d get after x units of time.

Natural Log is about time

The natural log is the inverse of e, a fancy term for opposite. Speaking of fancy, the Latin name is logarithmus naturali, giving the abbreviation ln.

Now what does this inverse or opposite stuff mean?

e^x lets us plug in time and get growth.
ln(x) lets us plug in growth and get the time it would take.

For example:

e^3 is 20.08. After 3 units of time, we end up with 20.08 times what we started with.
ln(20.08) is about 3. If we want growth of 20.08, we’d wait 3 units of time (again, assuming a 100% continuous growth rate).

With me? The natural log gives us the time needed to hit our desired growth.

Logarithmic Arithmetic Is Not Normal

You’ve studied logs before, and they were strange beasts. How’d they turn multiplication into addition? Division into subtraction? Let’s see.

What is ln(1)? Intuitively, the question is: How long do I wait to get 1x my current amount?

Zero. Zip. Nada. You’re already at 1x your current amount! It doesn’t take any time to grow from 1 to 1.

ln(1) = 0.

Ok, how about a fractional value? How long to get 1/2 my current amount? Assuming you are growing continuously at 100%, we know that ln(2) is the amount of time to double. If we reverse it (i.e., take the negative time) we’d have half of our current value.

ln(.5) = – ln(2) = -.693

Makes sense, right? If we go backwards (negative time) .693 seconds we’d have half our current amount. In general, you can flip the fraction and take the negative: ln(1/3) = – ln(3) = -1.09. This means if we go back 1.09 units of time, we’d have a third of what we have now.

Ok, how about the natural log of a negative number? How much time does it take to “grow” your bacteria colony from 1 to -3?

It’s impossible! You can’t have a “negative” amount of bacteria, can you? At most (er… least) you can have zero, but there’s no way to have a negative amount of the little critters. Negative bacteria just doesn’t make sense.

ln(negative number) = undefined

Undefined just means “there is no amount of time you can wait” to get a negative amount.

Logarithmic Multiplication is Mighty Fun

How long does it take to grow 4x your current amount? Sure, we could just use ln(4). But that’s too easy, let’s be different.

We can consider 4x growth as doubling (taking ln(2) units of time) and then doubling again (taking another ln(2) units of time):

Time to grow 4x = ln(4) = Time to double and double again = ln(2) + ln(2)

Interesting. Any growth number, like 20, can be considered 2x growth followed by 10x growth. Or 4x growth followed by 5x growth. Or 3x growth followed by 6.666x growth. See the pattern?

ln(a*b) = ln(a) + ln(b)

The log of a times b = log(a) + log(b). This relationship makes sense when you think in terms of time to grow.

If we want to grow 30x, we can wait ln(30) all at once, or simply wait ln(3), to triple, then ln(10), to grow 10x again. The net effect is the same, so the net time should be the same too (and it is).

How about division? ln(5/3) means: How long does it take to grow 5 times and then take 1/3 of that?

Well, growing 5 times is ln(5). Growing 1/3 is -ln(3) units of time. So

ln(5/3) = ln(5) – ln(3)

Which says: Grow 5 times and “go back in time” until you have a third of that amount, so you’re left with 5/3 growth. In general we have

ln(a/b) = ln(a) – ln(b)

I hope the strange math of logarithms is starting to make sense: multiplication of growth becomes addition of time, division of growth becomes subtraction of time. Don’t memorize the rules, understand them.

Using Natural Logs With Any Rate

“Sure,” you say, “This log stuff works for 100% growth but what about the 5% I normally get?”

It’s no problem. The “time” we get back from ln() is actually a combination of rate and time, the “x” from our e^x equation. We just assume 100% to make it simple, but we can use other numbers.

Suppose we want 30x growth: plug in ln(30) and get 3.4. This means:

e^x = growth
e^3.4 = 30

And intuitively this equation means “100% return for 3.4 years is 30x growth”. We can consider the equation to be:

$\displaystyle{e^{x} = e^{rate \cdot time}}$

$\displaystyle{e^{100 \% \cdot 3.4 years} = 30}$

We can modify “rate” and “time”, as long as rate * time = 3.4. For example:

3.4 years at 100% = 3.4 * 1.0 = 3.4
1.7 years at 200% = 1.7 * 2.0 = 3.4
6.8 years at 50% = 6.8 * 0.5 = 3.4
68 years at 5% = 68 * .05 = 3.4

Cool, eh? The natural log can be used with any interest rate or time as long as their product is the same. You can wiggle the variables all you want.

Awesome example: The Rule of 72

The Rule of 72 is a mental math shortcut to estimate the time needed to double your money. We’re going to derive it (yay!) and even better, we’re going to understand it intuitively.

How long does it take to double your money at 100% interest, compounded every year?

Uh oh. We’ve been using natural log for continuous rates, but now you’re asking for yearly interest? Won’t this mess up our formula? Yes, it will, but at reasonable interest rates like 5%, 6% or even 15%, there isn’t much difference between yearly compounded and fully continuous interest. So the rough formula works, uh, roughly and we’ll pretend we’re getting fully continuous interest.

Now the question is easy: How long to double at 100% interest? ln(2) = .693. It takes .693 units of time (years, in this case) to double your money with continuous compounding with a rate of 100%.

Ok, what if our interest isn’t 100% What if it’s 5% or 10%?

Simple. As long as rate * time = .693, we’ll double our money:

rate * time = .693
time = .693/rate

So, if we only had 10% growth, it’d take .693 / 10% or 6.93 years to double.

To simplify things, let’s multiply by 100 so we can talk about 10 rather than .10:

time to double = 69.3/rate, where rate is assumed to be in percent.

Now the time to double at 5% growth is 69.3/5 or 13.86 years. However, 69.3 isn’t the most divisible number. Let’s pick a close neighbor, 72, which can be divided by 2, 3, 4, 6, 8 and many more numbers.

time to double = 72/rate

which is the rule of 72! Easy breezy.

If you want to find the time to triple, you’d use ln(3) ~ 109.8 and get

time to triple = 110 / rate

Which is another useful rule of thumb. The Rule of 72 is useful for interest rates, population growth, bacteria cultures, and anything that grows exponentially.

Where to from here?

I hope the natural log makes more sense — it tells you the time needed for any amount of exponential growth. I consider it “natural” because e is the universal rate of growth, so ln could be considered the “universal” way to figure out how long things take to grow.

When you see ln(x), just think “the amount of time to grow to x”. In an upcoming article I’ll bring e and ln together, and the sweet aroma of math will fill the air.

Appendix: The Natural Log of E

Quick quiz: What’s ln(e)?

The math robot says: Because they are defined to be inverse functions, clearly ln(e) = 1
The intuitive human: ln(e) is the amount of time it takes to get “e” units of growth (about 2.718). But e is the amount of growth after 1 unit of time, so ln(e) = 1.

Think intuitively.

124 Comments

Posted May 20, 2007, under Math
Tags:
Related Posts:

An Intuitive Guide To Exponential Functions & e

Explanations for everyone.

How to Develop a Mindset for Math

Developing Your Intuition For Math

A Visual Guide to Simple, Compound and Continuous Interest Rates

Like it? Share on:

RSS or Email Subscription |

Print This Post

124 Comments »

Trackbacks & Pingbacks

Pingback by How to Develop a Mindset for Math | BetterExplained — November 27, 2007 @ 4:11 am
Pingback by strawberry fields forever « Meniti di Titian Hati — April 30, 2008 @ 4:27 am
Pingback by A Gentle Introduction To Learning Calculus | BetterExplained — May 3, 2008 @ 9:20 am
Pingback by Developing Your Intuition For Math | BetterExplained — January 8, 2009 @ 1:09 pm
Pingback by 最近的最近 at 奔三 — February 8, 2009 @ 2:46 am
Pingback by Complex Concepts, Explained Better » Lone Gunman — February 12, 2009 @ 2:26 am
Pingback by Better Explained « Xavier Seton’s Blog — May 7, 2009 @ 12:40 am
Pingback by Shooting the moon « Underage Reading — September 5, 2009 @ 4:32 pm

Comments

Uhm, wouldn’t bacteria grown at 100% per day take more than 3 days? first day gives you 2x growth, second gives you 4x, third gives you 8x, sometime after 3rd but before 4th gives you 10x. Perhaps .3 days, dunno.
Sorry, I couldn’t read past that seemingly huge error.

Mike Y — May 21, 2007 @ 12:49 pm
Ah, that’s the magic of continuous compound growth. Consider how much bacteria you have at the 12-hour mark: 1.5 (50% more than you started).

After another 12 hours that amount (1.5) has time to grow another 50%: 1.5 * 1.5 = 2.25, even better than double at the end of the day.

Now take a smaller interval, like 6-hours. After 6 hours you have 25% growth: 1.25

and after 4 periods of 25% growth you have 1.25^4 = 2.44 times your original.

If you keep taking smaller and smaller time intervals, you get a net compound growth rate of 2.71828 per day, which is e (take a look at the article on e for more details). I’ll amend the article to clarify.

Kalid — May 21, 2007 @ 1:15 pm
Perhaps, but that’s NOT what you said, you said they had 100% growth in 1 day. You didn’t say 125% growth in 1 day.

Mike Y — May 22, 2007 @ 4:51 am
The example you’re giving seems to be based on compounding interest; if you have a 5% interest rate (yearly) BUT you compound it continously you get an APR or whatever of 5.25% or whatever. Basically it works out that ln would be useful IF you wanted to take something that didn’t compound continously, and see what would happen if it did. By definition, a 100% increase in a colony of bacteria in 24 hours means that it will actually have double in size in 24 hours. Yes it would have been growing continously, but the end result would be 100% growth, not e^1.

Mike Y — May 22, 2007 @ 4:58 am
That’s a good point, I think I’ll rephrase the bacteria example to use money, where the concepts of “simple” and “compound” interest are more natural.

You can imagine bacteria that grows at 100% “simple interest”, and the net result would be over 100% growth if the mini-bacteria which are made after a half-day create new bacteria of their own. But describing it as 100% continuous growth, as worded, may be confusing.

The meta-point, which I’m pretty sure we both agree on, is that ln can give you the time something growing continuously (e^x) would take.

And the cool thing is that ln can even help figure out non-continuous growth (2^x, like the normal bacteria case) as well. I’ll be writing more on this.

Kalid — May 22, 2007 @ 12:06 pm
I’m not sure that I agree on the “something” grows part. It doesn’t really seem to apply to anything more than interest, or something I can’t think of that might not grow in cleanly divisible increments. As for the ln being useful for the bacteria growth, actually not all. That would be Log base 2 rather than Log base e.

Mike Y — May 22, 2007 @ 12:57 pm
Uh oh, you’re going to make me give away the crown secret: e and ln can be used in a change-of-base formula, so you actually don’t need a separate log base 2 to get the expected number of doublings (It’s convenient to have a separate log base 2, but not strictly needed).

Kalid — May 22, 2007 @ 1:36 pm
excellent explanation…its more intuitive now!

raj mathur — May 23, 2007 @ 1:34 pm
Thanks Raj, glad you liked it!

Kalid — May 23, 2007 @ 5:27 pm
Wow… i’ve been casually using ln(N) in the context of “big-O notation” in programming for years, but this article is the first to really get my on my way to being able to USE the function. i first tried the related Wikipedia articles and, like you mentioned, was only mystified by the circular references between ln and ‘e’.

Stephan Beal — June 24, 2007 @ 12:22 am
Hey Stephan, thanks for the mail! There’s so many topics that we just take for granted and use mechanically, it’s a lot of fun to really understand them. E and natural log was like this for a long time for me, too.

Kalid — June 24, 2007 @ 11:12 pm
Hi my friend… congratulations for an amazing site! This is the way these things should be taught to children! Will be spreading the word to as many people as I can! Since you’re into e, I wonder if you could write something demystifying a bit hyperbolic trigonometry.

John — July 3, 2007 @ 3:55 pm
Thanks John, I’m happy you liked the site! I think hyperbolic geometry would be a good topic — personally, I need to investigate it a bit more! But I’d love to share what I learn when I do.

Kalid — July 15, 2007 @ 2:15 am
Excellent article.cool..Maths was never so easy to read.

Amit — July 31, 2007 @ 1:26 am
ln(a*b) = ln(a) + ln(b)

The log of a times b = log a + log b. This relationship makes sense when you think about it being the time to grow.

If we want to grow 30x, we can wait ln(30) all at once, or simply wait ln(3), to triple, then ln(10), to grow 10x again. The net effect is the same, so the net time should be the same too (and it is).

this is very well said;
i don’t know that i’ve ever
seen it put in quite this way.

on the other hand, you’ve confused
the issue mightily by referring
to “simple interest” — which is
essentially the opposite
of “compound interest” and hence
not what you mean at all.

wikipedia on interest

vlorbik — August 1, 2007 @ 11:20 am
Hi vlorbik, thanks for the comment and feedback. I’d like to understand what you mean about simple interes vs. compound to help make the article more clear.

For me, I consider continuous interest an extension of simple interest, rather than the opposite. Simple interest has a relatively large term (interest returned over 1 year), while compound interest breaks the duration into many (infinitely small) pieces.

My meaning was that ln(30) means a period of continuous growth for 1n(10) units of time, followed by a period of continuous growth for ln(3) units of time.

Kalid — August 2, 2007 @ 3:51 pm
I don’t understand the comment about conversion between simple and compound interest (as described below). If, ln(rt) = ln(2) = .693, then .693…/r should exactly equal the time it takes to double.

Since .693 is approximated by .72, there is some error in this shortcut, but it is not a function of a conversion from compound to simple interest. Please elaborate on your thinking.

One caveat: notice how we’re converting between simple and compound interest – won’t this mess up our formula? Yes, it does, but at reasonable interest rates like 5%, 6% or even 15%, there isn’t much difference between simple and compound interest. So the rough formula works, uh, roughly.

Anonymous — August 22, 2007 @ 12:35 pm
Hi, great question. Simple vs. compound interest is pretty tricky and I want to clarify it in a later article.

There are two sources of error in the rule of 72 equation:

1) The rounding from .693 to .72
2) The use of natural log when most interest is actually simple interest. The natural log (ln) assumes continuous growth, but this is not the case for most returns.

Suppose you have an investment with 5% simple interest.

To compute your return, you get $100 * (1 + .05) = $105 after the first year.

To compute your return with compound interest, you’d have $100 * e^(.05) = $105.13 at the end of the year.

It’s only 13 cents, but it’s a difference that can lead to small errors in how long growth rates will take. (For small rates like 5%, simple vs compound interest isn’t a big deal. For larger rates like 100%, simple interest would be $200, while compound interest would be “e”: $271.281828)

I do need to take another look at all this and make sure my explanation is correct, it can be confusing

Kalid — August 23, 2007 @ 2:36 am
Your article was very useful and helped me better understand the natural logarithm.
Thanks!
Julien.

Julien — September 10, 2007 @ 1:10 am
Hi Julien, I’m glad you found it useful!

Kalid — September 11, 2007 @ 9:55 pm
The concept is so clear now! and the explanation is just awesome. Keep up the good work.

Jason.B — October 8, 2007 @ 12:13 am
Thanks Jason!

Kalid — October 8, 2007 @ 8:07 am
This website makes sense of the things that even math teachers have to look up to do correctly.
Amazing job Kalid, absolutely amazing.

Anonymous — October 21, 2007 @ 11:11 pm
Wow, thanks for the kind words! I’m happy to be able to share my thoughts, I’m glad you enjoyed the site .

Kalid — October 22, 2007 @ 1:10 am
e^3 is 20.08. After 3 units of time, we end up with 20.08 more than we started with.

Should that read “we end up with 20.08 times what we started with?”

Scott — December 1, 2007 @ 8:56 pm
Whoops, that was unclear. Yep, it should be 20.08 times our initial amount. I’ll fix it up.

Kalid — December 1, 2007 @ 9:21 pm
Very informative and helpful. I would appreciate it if you could explain how you would solve this problem.

Investor A invests $1000 at an interest rate of 5% compounded continuously and Investor B invests $500 at a rate of 8% compounded continuously. If both of them invest at the beginning of 2008, when will the value of their investments be equal ?

Dave — December 4, 2007 @ 6:30 am
Can someone explain to me how e^(pi*i) = -1?

dasickis — December 4, 2007 @ 11:36 am
@Dave: Nice question. You basically want to solve this equation:

1000 * e^(.05 * t) = 500 * e^(.08 * t)

e^(.05*t) is how much growth the $1000 investment has after some amount of time, and similar for e^(.08 * t). If you take the natural log of both sides you can “cancel” the ‘e’ and solve for the amount of time needed.

@dasickis: Great topic, I’m planning on covering that eventually. First I’ll be writing about what complex numbers mean. I found a good explanation here: http://www.cut-the-knot.org/arithmetic/algebra/Scott.shtml.

Kalid — December 4, 2007 @ 11:50 am
This was a very informative site. It really cleared up all the bad blood between me and logarithms.

Brandon — December 7, 2007 @ 8:00 am
You know what? This site was just sooo good that I have to leave another comment. Thank you for this fabulous site.

Brandon — December 7, 2007 @ 8:04 am
sorry…it’s fabolous. Not fabulous

Brandon — December 7, 2007 @ 8:07 am
Thanks Brandon

Kalid — December 7, 2007 @ 9:20 pm
Cool is the word that comes to mind. Man and all these years I thought that these were some abstract concepts both ln and e. Thanks for letting us appreciate what they really are. I really keep looking forward to your new articles on math .I seriously suggest that you write a book on math and if you dont have the time then take some out of your schedule to write one …..

Mohammad Ali — December 11, 2007 @ 11:05 pm
Thanks Mohammad! There’s so much beauty in math, but it gets buried under lifeless proofs. People forget that these ideas emerged naturally, not by someone saying “Today I’ll define e as lim n->inf of (1+1/n)^n”.

I’ve been thinking about taking the top math/programming posts and putting them into a book… I think it’d be fun. Not quite enough yet, but soon .

Kalid — December 12, 2007 @ 12:56 pm
Thanks a lot! Before finding this site, I was trying to understand the meaning of ln and e on Wikipedia, and discovered the same circular logic that you mentioned. Keep up the good work! I look forward to future articles.

Thomas — January 13, 2008 @ 10:49 pm
Thanks Thomas, glad you enjoyed it. I had that same run-around for a while myself.

Speaking of new articles, I just did a post on interest rates.

Kalid — January 14, 2008 @ 12:35 am
Wow – THANK YOU for putting this so simply!!! My friend used this term on the phone earlier. Since I had no clue what it meant, I went to Wikipedia and saw a horribly complicated, technical explanation -but you put it simply!! And true wisdom is being able to communicate a complex topic in simple terms. THANK YOU so much. You made my night!!

Mimi — January 17, 2008 @ 8:18 pm
Hi Mimi, thanks for the wonderful comment! I’m glad you found it helpful — I agree, there are many subjects that are often explained in an overly complex way. Everything can (and should) be simple .

Kalid — January 18, 2008 @ 12:02 am
Do all bases for logs have to be positive? If not is the log of a negative number possible?
EG -8 = (-2)^3
Is this ‘log to base -2, of -8 = 3
Help please and thanks. JP

jack paton — January 26, 2008 @ 8:01 am
Hi Jack, great question. At its heart, a logarithm answers the question

base^power = desired value

So I don’t see a reason why you couldn’t use a negative base. The only problem is that certain values are undefined: with regular, positive bases we can’t get to negative values (at least, not without using imaginary numbers).

With negative bases, certain values are out of range: for example, we can’t get “-4″ since (-2)^2 = 4.

So, negative bases would work, but would have a different set of undefined values.

Kalid — January 26, 2008 @ 12:00 pm
I really like the way you explain about e,you make a really good teacher

Doug — February 12, 2008 @ 1:04 pm
Thanks Doug, glad you liked it!

Kalid — February 13, 2008 @ 12:41 am
Excellent explanation…logical, applicable, and concise. I teach nuclear plant operators a variety of technical subjects/skills (including mathematics), and this is the type of format I strive for in my lessons. Less memorization and more in-depth understanding means more retention! I am going to recommend your site to both my students and my fellow instructors.

Tim — February 13, 2008 @ 11:27 am
Wow, thanks Tim, that’s great! I love hearing that people in the real world are finding the content useful.

Kalid — February 13, 2008 @ 11:56 am
The world make’s sense again – you just reminded me why i like math…
thank you!
kt

Katie — April 15, 2008 @ 12:30 pm
Awesome Katie, glad you enjoyed it!

Kalid — April 15, 2008 @ 3:22 pm
Re: comment #41: saying that “certain values are undefined” is IMO somewhat misleading. If you would allow negative bases, such as -2, you would get a very ‘messy’ function.

If you realise the log is the inverse of an exponential function with the same base, allowing -2log(x) would be the same as allowing -2 as the base in an exponential function: y = (-2)^x.
Now this last function is only defined for integer x: (-2)^0.5 for example is asking for the square root of -2 which clearly is undefined (assuming non-complex numbers). So the graph of (-2)^x consists of dots which are horizontally spaced 1 apart (alternating above and below the x-axis: the sequence (-2)^1, (-2)^2, (-2)^3 is -2, +4, -8, +16, etc).
Likewise the graph of log(x), base -2, would consist of dots vertically spaced 1 apart and alternating left and right of the y-axis (-2log(-2) = 1, -2log(4) = 2, -2log(-8)=3, etc) — the reflection of (-2)^x in the line y=x.

So yes, you’re right that “certain values are out of range”. The problem though is that *almost all* values are out of range, seriously limiting the usefulness of a log function with negative base. There’s a good reason mathematical practice explicitly limits the choice of a base for log and exponential functions to positive numbers (excluding 1, for obvious reasons).

Your remark that “I don’t see a reason why you couldn’t use a negative base” seems to me to add confusion rather than clear things up.

Somewhat related observation: when dealing with discrete sequences, all the above is not a problem. You can easily define a sequence x(0) = 1, x(n) = -2*x(n-1), giving the sequence 1, -2, 4, -8, … This demonstrates how such a sequence resembles but is not identical to exponential growth.

Don’t take my comments to be negative though: I really enjoy your website, including the above article.

Hendrik Jan — April 17, 2008 @ 3:02 am
Hi Hendrik, thanks for the comment! No worries, lively discussion is one of the fun parts of having a blog. Nobody has all the answers or is immune from mistakes .

Yes, looking at it again I should have clarified my response to the negative base. As you say, while it is “possible” to have a negative base, it’s likely not very useful because it only works for a small set of numbers. (As an aside, a negative base may give an interesting graph if you trace out the complex numbers it covers). Appreciate the comment.

Kalid — April 17, 2008 @ 9:33 pm
Your detailed content really shine. Yours is one of the few that has an in-depth explanation. Maths is, at times, abstract and takes time to figure out the concepts. Here I find it smooth going. Though I have maths blog myself, I like your blog. Good work! Nice learning from you. Natural log and time…. cheers!

Lim Ee Hai — April 20, 2008 @ 6:11 am
your presentation is very good. it has a practical
insight, but when you come up with 2^n for the doubling equation you seem to pull that out of the hat. for sombody familiar with math its easy to see why but for sombody unfamiliar its mysterious. how did you get there? then you pull out the 100% again how did you get there? then you use the 2^n equation for all other forms. i understand why but i could never derive this and wonder that there is still somthing i dont get.

mike l — April 25, 2008 @ 9:59 pm
@Lim Ee Hai: Thanks for the wonderful comment! I’m glad you’re finding the site useful. Yes, math has many beautiful ideas, but they can get hidden behind a wall of abstraction, or lost in a sea of formulas. Glad you’re enjoying it.

@Mike: Great question, it’s always helpful to see what parts worked and what didn’t. There’s more about the 2^n equation in the article on e, but I’ll try to explain it here.

Doubling can be considered as growing 100% — if you start the year with 1 item, you finish with 2. So 2 = (1 + 100%).

If you double 3 times, you could write that as 2 * 2 * 2. That is, after 3 years, you would have 8 items.

But since exponents are a shortcut for repeated multiplication, we can write 2^3 instead of 2 * 2 * 2. Even better, we can pick any number of years and write

2^n

where n is the number of years to use. Remembering that 2 implies a rate of 100% increase, we could replace that with

(1 + rate)^n

to get a general equation for any rate and duration. You may also want to try this article on interest rates.

Hope this helps!

Kalid — April 25, 2008 @ 11:28 pm
I am going to create my own world now!

Bobby Noble — May 11, 2008 @ 12:33 pm
Kalid –

Great explanation and very helpful. Thanks for taking the time to put it together.

David

David Charlot — May 29, 2008 @ 6:33 am
Hi David, appreciate the comment — I’m glad the explanation worked for you!

Kalid — May 29, 2008 @ 9:05 am
Thank-you! I have a degree in math I have wondered for years why e was used. In all of my classes I was told what e equaled, that ln was the inverse of the e function, and how to compute with e and ln, but never how e was derived! I now have a better understanding and hopefully this will make me a better math teacher in the future!

Rhonda — June 1, 2008 @ 4:58 pm
Hi Rhonda, I’m so happy you found the article useful! Yes, there are many concepts that just get thrown out there without the background about *why* it’s useful.

e/ln aren’t magical, just the result of wondering what would happen if you earned interest as fast as you could (i.e. compounding every fraction of a second). Good luck with your teaching!

Kalid — June 1, 2008 @ 9:30 pm
Does this make sense? Mike Y said all that about simple vs continuous, and how could it be continuous if it’s simple. But think of the bacteria: If one bacterium can split in one hour, it will have a growth rate of 2, not e, because half of the bacterium cannot start splitting until it is completely split right? Wouldn’t that be the same for populations, so e only applies to things that grow continuously.

Trying to understand — June 18, 2008 @ 2:14 pm
I guess I’m wondering, how could a population increase by 1.5, wouldn’t all the bacteria take the entire day to split, or if each were offset, you couldn’t count the incomplete bacteria in the total.

Trying to understand — June 18, 2008 @ 2:18 pm
The thing is, if bacteria divided more than once per day, the rate would be greater than 100% per day, but they can’t divide continuously regardless, the time it takes a bacteria to divide would be the time it takes a population to double. I don’t see how this relates to continuous compounding

Trying to understand — June 18, 2008 @ 2:22 pm
oh your article on e explains the difference between bacteria and money

Trying to understand — June 18, 2008 @ 2:36 pm
can someone tel me how to solve the logarithm of a negative number… for example log of -1 to the base 10… i know that the answer is a complex number…

log — June 23, 2008 @ 4:03 am
Great question. You can plug in negative logs to google calculator and do ln(-1) / ln (10). So log base 10 of -1 is about 1.36i.

Euler’s Formula explains how to do negative logs, and I’ll cover this in a future article .

Kalid — June 23, 2008 @ 9:11 am
@Trying to understand: Yep, money and bacteria grow differently (simple vs. compound). However, even bacterial growth can be modeled continuous growth at a different rate. And in reality, there are millions of bacteria at different stages, so the total “clump” looks like one continuously changing amount.

Kalid — June 23, 2008 @ 9:13 am
This site is amazing. I have a math degree from a fancy school and I never really understood ln until now. Thanks so much!

Louis — June 26, 2008 @ 8:27 am
Thanks Louis! Yes, sometimes it’s easy to miss the real insights when learning a subject at a deep level. Personally, I’m pretty interested in math and am trying to study analysis, hopefully some “aha” insights will click there .

Kalid — June 26, 2008 @ 10:50 am
cheers man, certinly cleared up some stuff for me. Wish I had this a few years ago at school. I think I get the discrete growth thing, but this really helped me with continuous change. Gonna help me in years to come. You should post on Wikipedia, the maths stuff there is inaccessable from a basic level of knowledge, whereas the article here is practical, much to my liking. Keep it up.

G04T_DFA — September 6, 2008 @ 3:51 am
First, let me say I think your explanation of ln is very intuitive and helpful.

However, your first example threw me off a bit because your terminology is incorrect with regards to simple interest. I see this is discussed a bit in the comments, but the following comment you made is incorrect: “For me, I consider continuous interest an extension of simple interest, rather than the opposite. Simple interest has a relatively large term (interest returned over 1 year), while compound interest breaks the duration into many (infinitely small) pieces.” In the financial world, simple interest means interest on the principal only, with no interest on interest. Compound interest means you get interest on the interest. It can be compounded quarterly, annually, continuously, etc. So constant growth is compound interest, compounded continuously. So, where you say compound interest, I believe you mean continuous compounding. And when you say simple interest, you still mean compounding, but it’s done an an annual or other discrete basis.

For reference see: http://en.wikipedia.org/wiki/Compound_interest

Mike — September 8, 2008 @ 2:08 am
@G04T_DFA: Thanks for the comment – glad you enjoyed it! Yeah, I make a few typo edits to Wikipedia every once in a while, but generally save the longer stuff for here .

@Mike: Thanks for the comment, you’re right: simple interest is like a fixed bond coupon with no reinvestment. As you noticed, I was really talking about the difference between yearly compound interest and continuously compounded interest. I’ll update the article — thanks for the catch!

Kalid — September 8, 2008 @ 9:15 pm
Thanks for your explanations of compound interest and from whence “e” is derived. Your explanation of compound interest would have saved me from an all night “do-it-by-hand” session 20 years ago. An accountant told me I was correct but it took a very long time to calculate the monies for at least four participants. Henceforth I’m referring a number of readers to you. If there’s anything wrong I’ll have ‘em sue you! Keep up the good work.

N. Kogneato — September 15, 2008 @ 8:32 pm
@N. Kogneato: I appreciate the comment, glad it was helpful! I might need to add a little disclaimer — “Results may vary” .

Kalid — September 16, 2008 @ 6:32 pm
Great write up on a useful concept. I work for an insurance company where we use LN to determine the time at which ‘losses’ or ‘investment’ income can/will grow over time. Our actuaries use various formulas that leverage LN and though I took calc in college, I couldn’t figure out the importance of the number. You’ve done what so many people don’t, shown the relevance of math to real world scenarios. Math, Accounting, and other fields are guilty of using jargon and obscure terms without ever explaining the impact of the terms in ‘real world’ tangible ways. I’ve passed this link on to other co-workers who have all found it useful. Thanks.

Brett — September 17, 2008 @ 6:42 am
@Brett: Thanks for the wonderful comment! Yes, I completely agree — we can end up using an idea for years in finance or engineering without understanding what it really means. It just becomes a magic equation we throw numbers into .

Glad you and your co-workers enjoyed it!

Kalid — September 17, 2008 @ 11:43 am
Great explanation for ln, but you already knew that…

I’m working on a problem in my quantum mechanics class, the Baker-Hausdorff lemma, and I can’t figure out how they’re expanding the series! Could you give me a point in the right direction?

z = ln [ (e^A)*(e^B ] = A + B + (1/2)(AB – BA) + (1/12)(A^2B + AB^2 – 2ABA + B^2A + BA^2 – 2BAB)

Is this some sort of twisted Taylor Series expansion?

BatManda — September 21, 2008 @ 12:23 pm
@BatManda: Thanks — great question. I don’t know much about that formula unfortunately, it does look like a crazy taylor series. It seems strange to break the equation apart when you could simplify it like this:

=ln[ e^(A+B) ]
= A + B

But clearly I must be missing something . You might try the math/physics forums (there’s a section for quantum): http://www.physicsforums.com/

Kalid — September 23, 2008 @ 12:13 am
First, let me say that I found your articles on e and ln to be very enlightening. Thanks for taking the time.

That being said, I agree with the general consensus that your explanation of 100% continuous growth is confusing. I’m not sure if this is valid for all uses of e, but I prefer to think of all cases of continuous growth to be 100% while only time varies. In this way, all talk of percentages can be left behind (as I’m not sure the concept of fractional continuous growth really applies to real world situations) and allows us to simply say “continuous growth.”

Also, I am surprised that no one mentioned the case of continuous growth that everyone who’s taken high school chemistry should know about: dG = -RT ln K which relates the reaction rate constant K to Gibbs Free Energy. Continuous growth is essential to any topic relating to chemistry including phase change, thermodynamics, heat and fluid transport phenomena, and a wide range of other topics. Math is a tool of science, not the other way around.

Luke — October 9, 2008 @ 10:06 am
what about the power property of natural logs.. how is this derived?

ln(b^t) = t ln(b)

this is a bit confusing to me

Anonymous — October 13, 2008 @ 5:54 pm
@Luke: Thanks for the comments! I think I need to revisit the continuous growth explanation as it can be really confusing. I see continuous growth of r% meaning:

* 1 unit will product r% interest after 1 time period
* That r% interest, as soon as it’s made, will produce r% on itself after 1 time period

So, the “money that money earns, earns money”.

The problem is the difference between APR (annual percentage rate — your “growth rate”) and APY (annual percentage yield — the total amount you change as a result of the compounded interest).

Because it’s e^r*t, you could see it as 100% growth letting time vary (as you mentioned), or 1 year letting the growth rate vary. But still, I need to think about ways to clarify.

Thanks for the relation to chemistry, it’s been a while since I’ve looked at that and it’s nice to have reminders .

@Anonymous: Great question. ln(b^t) means: How long does it take to grow to b^t?

Well, growing to b takes ln(b) time (for example, growing to 3 takes ln(3) time). Growing to b*b takes ln(b) + ln(b) time [grow to b, then grow to b again -- to grow to 9, you grow by 3, then grow by 3 again].

So, growing to b^t means you just add up the time to grow to b [ln(b)] “t” number of times: t * ln(b). Hope this helps!

Kalid — October 18, 2008 @ 3:36 pm
I’m taking a financial structuring course at an undergraduate level… always knew how to use e but never really grasped what the hell it meant! thanks a lot for this it really helped refresh and consolidate my knowledge of this function!

thanks again!

RP — October 22, 2008 @ 12:07 pm
@RP: You’re welcome, I’m glad you enjoyed it! The true meaning of e didn’t hit me until much longer after I “learned” it also .

Kalid — October 22, 2008 @ 5:17 pm
Many research papers use the natural log for items such as total assets or sales revenue as a size variable. Why is the natural log a better size measure versus just using the actual dollar amounts for total assets?

Phil

phil little — November 14, 2008 @ 1:59 pm
Hi Phil, good question. I’d be surprised to see natural log taken on a straight number (total assets or sales) — usually it’d be used for a growth factor or a series. It could be used to rescale numbers to a “human” factor (like a Richter scale or Decibel lets us talk about large variations in a smaller range). But there may be another interpretation of the natural log which would make sense for the raw number.

Kalid — November 14, 2008 @ 11:38 pm
U’m In Pre-Calc and sadly when the teacher talks thats all she does I get better explinations from other students, and this was a new topic, which of couse i thaught i would never grasp thank you for this…:(…i sorta wish you could teach me now…but i digress and return to theact of thanking you and hope that you cover some other topics i’ll have to come.

Kid Crew — November 19, 2008 @ 3:51 pm
I just want to THANK YOU because your article was so just so much more straight forward then my text book. This article explained the concepts and a more comprehensive way then I think even my teacher could explain it. THANK YOU AGAIN and keep wrtiting!

Calculous Crushed — December 3, 2008 @ 8:34 pm
@Kid Crew: Glad you enjoyed it! Hopefully I’ll cover the topics you’re learning about. Really happy to hear things are clicking.

@Calculous Crushed: You’re welcome! I had a similar reaction when learning about logs and exponents, and only “got” them much, much later after learning about them. Thanks again for the encouragement.

Kalid — December 4, 2008 @ 2:23 am
I dont quite get the the rule of 72 thing could explain that to me. I dont get the idea of having rate and time always getting the same answer.
Thank you. (great article, btw)

Anurag C — January 3, 2009 @ 3:50 am
@Anurag: There’s more detail on the Rule of 72 here:

http://betterexplained.com/articles/the-rule-of-72/

Kalid — January 4, 2009 @ 1:23 pm
Can you please explain how log returns work (ie IBM starts the day at $5 and finishes the day at $6…the return would equal ln(6/5))…i believe this type of calculation is used in finance to calculate returns. This is different than (6-5)/5….I understand the log is using continous growth, but can you explain how to think about it, and also why most firms use one technique rather than the other.

jeff — January 5, 2009 @ 2:18 pm
Hi Jeff, interesting comment! I’m not certain of the reason, but here’s what comes to mind.

e and natural log let us discuss growth in a way that is “flexible”. Using your example, (6-5)/5 represents 20% growth in a day. ln(6/5) ~ 18%, which is the equivalent continuous growth rate (which is less than 20% because continuous growth earns “interest on interest” and can catch up).

With the continuous growth rate, we can say that having 18% growth for 1 day will have the same impact as 1% growth for 18 days. Or 2% for 9 days, or 3% for 6 days, etc.

If we use 20% standard growth, we can’t easily swap out the numbers since rate and time can’t be mixed. Natural log lets us convert rates to “standard” format which makes it easier to do mental “what-if” scenarios. That’s one application I can think of .

Kalid — January 5, 2009 @ 8:18 pm
Hi Kalid, brilliant explanation, really enjoyed it.

I was thinking about cell division.

If I understand correctly, we cannot use our formulas if there are less than 100 cell divisions over the time period under consideration; if there are less than 100 cell divisions the formulas will be too inaccurate.

See Kalid’s explanation here

If the cell could divide in zero seconds then our formulas using e would be 100% accurate.

A cell division every zero seconds corresponds to a growth rate of infinity%

Using our formula above The time for the cells to double would be given by
time x infinity = ln(2)

time = zero seconds.

This is a trivial result, but ironically this is the only time the formulas are 100% accurate.

The rest of the time, when we are dealing with real life systems, the formulas are so close to accurate that errors can be ignored.

Have I got it or am I way off the mark?

chris — January 11, 2009 @ 4:17 am
Yes yo, bn a great pleasure reading the article. It opened me up a bit, thanx to you proficiency.I wish to kindly ask if you can be able to explain to me how to hanndle exprassions of the form :Ln(x+y). Just how this can be simplified will do me good.
Thanx in advance!

Sehluko — January 16, 2009 @ 12:29 am
@chris: Great question! Here’s the key:

Real-life systems can’t grow perfectly continuously. But, they can be approximated by some continuous function.

An analogy may be how we try to make wheels on a car “round” — that is, follow the equation of a circle (x2 + y2 = r2). Of course, at a molecular level the atoms aren’t exactly on that line, but the above equation describes the shape of the wheel very well.

For cell divisions, individual cells may not divide at a continuous rate (or even at 100 times per second). But the whole “lump” of cells may appear to grow at some rate — we have a lumpy goop that is growing over time.

e^x can then approximate the “expected” growth rate of that goop, like the circle can model the “expected” location of atoms in the wheel. So, you don’t need your cells to grow at any certain rate, you can find some rate that approximates the way it grows. You can find some growth rate x to make e^x fit the curve of your actual growth. If your goop grows 2x after a unit of time, your equivalent continuous rate is ln(2) = .69, and can be modeled by e^.69x. Hope this helps!

@Sehluko: Hi, I’m not sure there’s an easy way to simplify ln(a+b) by itself. If there are other terms ln(a+b) + ln(c+d) you can do = ln([a+b]*[c+d]).

Kalid — January 17, 2009 @ 9:01 pm
Kalid,

Great work.

Question: as you know, we think of risk and return in finance. Let’s assume we have an expected rate of return (on which we can apply e assuming the rate is constant or close to constant). But let’s further assume that returns are uncertain and normally distributed around the mean (with a known variance). As my variance in returns increases, what happens to e?

Thanks!

David

David — January 18, 2009 @ 9:28 pm
Yay! I love math. Thanks to these wonderful lessons.

Christian — January 19, 2009 @ 4:44 am
Thanks for your article. It helped a tremendous amount. My unit guide describe all of ln and e within one side of a standard a4 piece of paper. It was incredibly useful! My unit jumped from ln and e into exponential and logarithmic models (Ln Reg). Thank you very much, and I’d be happy to read more!

Raymond — January 19, 2009 @ 9:07 pm
Hi Kalid
thanks so much for your response. What I was trying to say is elaborated below:

Let us say we have a sum in the bank invested at 100% growth per year compounded every 6 months. If we dive straight in with our formulas involving e we would say:

We have 100% growth over 1 year rate x time = 1
Therefore growth factor = e^1 = 2.71828182846

However using our compound growth formula:

Growth factor = (1 +1/2)^2 = 2.25

A fair size inaccuracy has crept in:

So we always have to be mindful of how many times the we have compounded over the period in question.

If there was continuous growth, of course, there would be no problem.

Now let us consider rates different from 100%; for example, a growth rate of 1% compounded 100 times over a year.

We can jump in with our e formula and say
that the growth factor will be:
e^(1/100) = 1.01005016708

However, if we use our compound growth formula we get a growth factor of:

(1+.01/100)^100 = 1.01004966209

Why the discrepancy?

Well let us recall how we derived the e formula for growth rates that are different from 100%

We said that a continuous compound could be approximated to a number of discrete compounds.

Applying this to the problem above: we will approximate 100 discrete compounds to 1 discrete compound.

In other words we are stating that:

1+.01/100)1^100 is close to

(1 + .01/1)^1

We then rearrange this to give:

(1 + 1/100)^(100x(1/100))

But (1+1/100)^100 is nearly e

so the answer must be e^(1/100)

right so let us examine the areas where we have allowed inaccuracies to creep in.

first we said:

1+.01/100)1^100 is close to

(1 + .01/1)^1

In fact it is a little bit larger

Then we said:
(1+1/100)100 is close to

e,

In fact it is a little smaller

So we’ve exaggerated in opposite directions allowing us to get an answer but it is an approximate one.

If we had continuous growth instead of our 100 discrete compounds over the time period in question, all of these inaccuracies would disappear.

We can see this if we look at the same problem again but with continuous growth over the year.

Let us approximate an infinite number of discrete compounds to 1000 compounds

The compound growth formula gives:

1+.01/infinity)^infinity

This is close to

(1 + .01/1000)^1000 (closer than the last approximation because the series converges.)

This can be rewritten as:

(1 + 1/10000)^(100000x(1/100))

making our e formula even more accurate because (1+1/10000)^10000 is closer to e than (1+1/100)^100

You can use your imagination to determine that as we approach continuous growth the e formulas become more and more accurate.

However very few systems in the real world exhibit continuous growth so caution must be exercised.

I am an amateur mathematician so this could be a load of rubbish please chip in with your two cents. Thanks for such a brilliant web site Kalid.

Chris — January 22, 2009 @ 3:07 pm
FWIW, in my class, the logarithm was defined as the antiderivative of 1/t, and the exponential map as the inverse of the logarithm.

Nimmy — February 11, 2009 @ 11:39 am
Mike Y, you are a stupid, stupid DlCK.

Telanis — February 13, 2009 @ 12:10 pm
Now the integral of 1/t = ln(t)

From Kalid’s explanation above that means that the (RATE x TIME) for something to grow, if it experiences continuously compounded growth, is given by the area under the 1/t graph from t = 1 to t = final size.

This can easily be shown mathematically but I was wondering if anyone has got a ‘better explained’ intuitive reason why the (RATE x TIME) for exponential growth is equal to the area under the 1/t graph.

Chris — March 4, 2009 @ 5:42 am
hey is there any laws dealing with natural logs over natural logs e.g ln|5 + 2x| / ln|5|?

Anonymous — March 11, 2009 @ 11:15 pm
Good job with the explanations. I do think a visual aid would be fantastic. A little graph. Maybe plotting y = ln x and y = e^x. Relating your explanations to a visual would certainly help me. I have had to read over and over some of your explanations (needing more clarity before moving on).
If you have time that is. Inbetween explaining other things.
Thank-you

John — March 30, 2009 @ 3:40 am
Further; You have not linked the concept of ln to e very well in terms of time to reach a certain level of growth. Consider the following

At 100% (continuous) growth, time to double can by definition of e: 2x = x.e^t, where x is the initial amount.

Lets get rid of x (/x to both sides): 2 = e^t
Using laws of logs: ln 2 = t ln e^1
ln e = 1, this leaves ln 2 = t

For those of ous who have a good understanding of ‘e’ gained from your last tutorial, this helps to tie it together. Hope you agree and consider it.
Thanks again

John — March 30, 2009 @ 5:02 am
assuming 100% growth rate, simplified statement?

e^(time) = amount
ln(amount) = time

explanation:
e^(time*100% growth) = amount (at 100% growth)

Aaron — April 3, 2009 @ 5:33 pm
Good job with the explanations. I do think a visual aid would be fantastic. A little graph. cheers

clearance london — April 14, 2009 @ 8:39 am
Good job with the explanations. I do think a visual aid would be fantastic.

platnosci online — April 21, 2009 @ 9:30 am
I am building an mapping application where I need to convert geolocation data (longitude / latitude) to x/y coordinates and vice-versa. I am having trouble understanding how I can solve for latitude given y using the Miller cylindrical projection method. I tried putting an image embed code below but if it doesn’t show up you can see the equation here: http://en.wikipedia.org/wiki/Miller_cylindrical_projection

I am interested in learning how to solve for this but the log math is still a bit abstract for me. Can anyone help clarify this problem?

Jorge — May 1, 2009 @ 11:26 am
Wow, I never liked math in school because I didn’t understand WHY the things like “e” and “ln” were practical. I guess I had a hard time memorizing mind-numbing formulas with teachers whom, I am guessing, did not even understand it quite so intuitively themselves. Thanks for sparking my interest in something I did not think I could effectively utilize in life.

phil — May 25, 2009 @ 7:17 am
@phil: Awesome! Yes, there’s so many things we learn by rote which can just kill our interest in a subject, glad you’re enjoying it again.

Kalid — May 26, 2009 @ 12:02 pm
Thanks for such a wonderful explanation of the exponential function and its inverse. I never understood how my calculus books came up with this number. Because they managed to avoid the “why’s” with rather unnecessary calculations and problems.

Thanks again for such a simple and intuitive explanation. This should be published!

awesome — July 23, 2009 @ 6:50 am
@awesome: Thanks for the wonderful comment! I’m happy it made sense to you after all this time, it was such a relief for me too when it finally clicked. And thanks, I hope to publish this one day .

Kalid — July 23, 2009 @ 11:40 am
I tutor college students. This is exactly the sort of explanation they need and I strive to provide. No, it’s not mathy/technical, thus it’s open to attacks from the “what ifs” and “but you fail to recognize” crowd. But this is the kind of explanation that will help the average student truly understand the concepts and–much more importantly–retain the information. Good job! I might even steal a couple of ideas from you. I hope you don’t mind.

Mike — August 28, 2009 @ 10:16 pm
@Mike: Thanks for the note, and you’re more than welcome to use the ideas here in your tutoring! I want to help as many people as I can to have that “aha” moment — glad you’re helping it along .

Kalid — September 4, 2009 @ 4:06 pm
I worship you!!! 12 years of grad school and 2 years of undergrad have not come close to what you have done here to help me understand

Anonymous — September 17, 2009 @ 8:37 pm
@Anonymous: I know what you mean! It took me a long, long time to really understand e / ln to a level that made intuitive sense!

Kalid — September 20, 2009 @ 12:21 am
how would you solve 8e^9t=12e^8t ?

amy — October 6, 2009 @ 12:14 pm
Man, I do not even know where to begin. I love your site and articles. e and ln articles are incredible, real art. In 5 min you have answered some questions that bugged me for years. You have amazing talent in teaching and I would love to see math/calculus book written by you some day. Engineers, computer science and math enthusiasts do not need “rigor”, they need real knowledge and understanding of the subject. And honestly I have never read anything even closely as good as what you have put on this site. Please keep it up!!!

RF_Guy — October 19, 2009 @ 6:46 am

RSS feed for comments on this post. TrackBack URI

Have a question? Know an explanation that caused your own a-ha moment? Write about it here.