The Pythagorean theorem is a celebrity: if an equation can make it into the Simpsons, I'd say it's well-known.
![]()
But most of us think the formula only applies to triangles and geometry. Think again. The Pythagorean Theorem can be used with any shape and for any formula that squares a number.
Read on to see how this 2500-year-old idea can help us understand computer science, physics, even the value of Web 2.0 social networks.
Understanding How Area Works
I love seeing old topics in a new light and discovering the depth there. For example, I realize I didn't have a deep grasp of area until writing this article. Yes, we can rattle off equations, but do we really understand the nature of area? This fact may surprise you:
The area of any shape can be computed from any line segment squared. In a square, our "line segment" is usually a side, and the area is that side squared (side 5, area 25). In a circle, the line segment is often the radius, and the area is pi * r^2 (radius 5, area 25 pi). Easy enough.
We can pick any line segment and figure out area from it: every line segment has an "area factor" in this universal equation:
![]()
| Shape | Line Segment | Area | Area Factor |
|---|---|---|---|
Square |
Side [s] | s2 | 1 |
Square |
Perimeter [p] | 1/16 p2 | 1/16 |
Square |
Diagonal [d] | 1/2 d2 | 1/2 |
Circle |
Radius [r] | pi r2 | pi (3.14159...) |
For example, look at the diagonal of a square ("d"). A regular side is $\frac{d}{\sqrt{2}}$, so the area becomes $\frac{1}{2} d^2$. Our "area constant" is 1/2 in this case, if we want to use the diagonal as our line segment to be squared.
Now, use the entire perimeter ("p") as the line segment. A side is $\frac{p}{4}$, so the area is $\frac{p^2}{16}$. The area factor is 1/16 if we want to use $p^2$.
Can we pick any line segment?
You bet. There is always some relationship between the "traditional" line segment (the side of a square), and the one you pick (the perimeter, which happens to be 4 times a side). Since we can convert between the "traditional" and "new" segment, it doesn't matter which one we use -- there'll just be a different area factor when we multiply it out.
Can we pick any shape?
Sort of. A given area formula works for all similar shapes, where "similar" means "zoomed versions of each other". For example:
- All squares are similar (area always $s^2$)
- All circles are similar, too (area always $\pi r^2$)
- Triangles are not similar: Some are fat and others skinny -- every "type" of triangle has its own area factor based on the line segment you are using. Change the shape of the triangle and the equation changes.
Yes, every triangle follows the rule "area = 1/2 base * height". But the relationship between base and height depends on the type of triangle (base = 2 * height, base = 3 * height, etc.), so even then the area factor will be different.
Why do we need similar shapes to keep the same area equation? Intuitively, when you zoom (scale) a shape, you're changing the absolute size but not the relative ratios within the shape. A square, no matter how zoomed, has a perimeter = 4 * side.
Because the "area factor" is based on ratios inside the shape, any shapes with the same "ratios" will follow the same formula. It's a bit like saying everyone's armspan is about equal to their height. No matter if you're a NBA basketball player or child, the equation holds because it's all relative. (This intuitive argument may not satisfy a mathematical mind -- in that case, take up your concerns with Euclid).
I hope these high-level concepts make sense:
- Area can be be found from any line segment squared, not just the "side" or "radius"
- Each line segment has a different "area factor"
- The same area equation works for similar shapes
Intuitive Look at The Pythagorean Theorem
We can all agree the Pythagorean Theorem is true (here's 75 proofs). But most proofs offer a mechanical understanding: re-arrange the shapes, and voila, the equation holds. But is it really clear, intuitively, that it must be a2 + b2 = c2 and not 2a2 + b2 = c2? No? Well, let's build some intuition.
There's one killer concept we need: Any right triangle can be split into two similar right triangles.
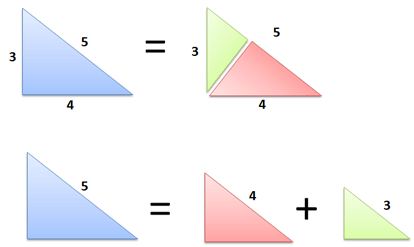
Cool, huh? Drawing a perpendicular line through the point splits a right triangle into two smaller ones. Geometry lovers, try the proof yourself: use angle-angle-angle similarity.
This diagram also makes something very clear:
- Area (Big) = Area (Medium) + Area (Small)
Makes sense, right? The smaller triangles were cut from the big one, so the areas must add up. And the kicker: because the triangles are similar, they have the same area equation.
Let's call the long side c (5), the middle side b (4), and the small side a (3). Our area equation for these triangles is:
![]()
where F is some area factor (6/25 or .24 in this case; the exact number doesn't matter). Now let's play with the equation:
![]()
![]()
Divide by F on both sides and you get:
![]()
Which is our famous theorem! You knew it was true, but now you know why:
- A triangle can be split into two smaller, similar ones
- Since the areas must add up, the squared hypotenuses (which determine area) must add up as well.
This takes a bit of time to see, but I hope the result is clear. How could the small triangles not add to the larger one?
Actually, it turns out the Pythagorean Theorem depends on the assumptions of Euclidean geometry and doesn't work on spheres or globes, for example. But we'll save that discussion for another time.
Useful Application: Try Any Shape
We used triangles in our diagram, the simplest 2-D shape. But the line segment can belong to any shape. Take circles, for example:
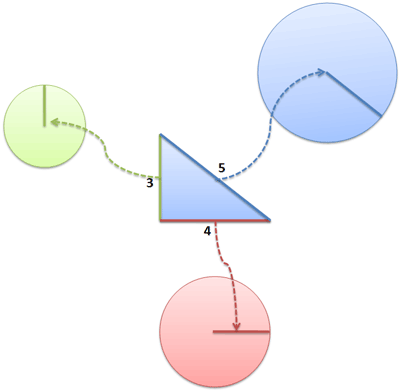
Now what happens when we add them together?
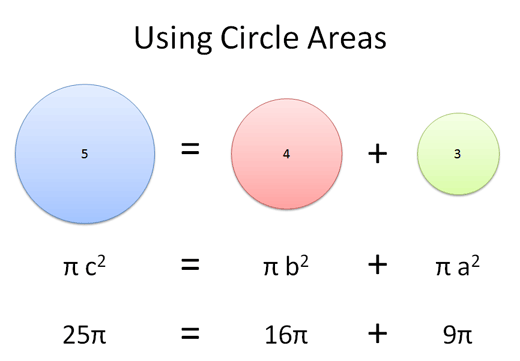
You guessed it: Circle of radius 5 = Circle of radius 4 + Circle of radius 3.
Pretty wild, eh? We can multiply the Pythagorean Theorem by our area factor (pi, in this case) and come up with a relationship for any shape.
Remember, the line segment can be any portion of the shape. We could have picked the circle's radius, diameter, or circumference -- there would be a different area factor, but the 3-4-5 relationship would still hold.
So, whether you're adding up pizzas or Richard Nixon masks, the Pythagorean theorem helps you relate the areas of any similar shapes. Now that's something they didn't teach you in grade school.
Useful Application: Conservation of Squares
The Pythagorean Theorem applies to any equation that has a square. The triangle-splitting means you can split any amount (c2) into two smaller amounts (a2 + b2) based on the sides of a right triangle. In reality, the "length" of a side can be distance, energy, work, time, or even people in a social network:
Social Networks.
Metcalfe's Law (if you believe it) says the value of a network is about n2 (the number of relationships). In terms of value,
- Network of 50M = Network of 40M + Network of 30M.
Pretty amazing -- the 2nd and 3rd networks have 70M people total, but they aren't a coherent whole. The network with 50 million people is as valuable as the others combined.
Computer Science
Some programs with n inputs take n2 time to run (bubble sort, for example). In terms of processing time:
- 50 inputs = 40 inputs + 30 inputs
Pretty interesting. 70 elements spread among two groups can be sorted as fast as 50 items in one group. (Yeah, there may be constant overhead/start up time, just work with me here).
Given this relationship, it makes sense to partition elements into separate groups and then sort the subgroups. Indeed, that's the approach used in quicksort, one of the best general-purpose sorting methods. The Pythagorean theorem helps show how sorting 50 combined elements can be as slow as sorting 30 and 40 separate ones.
Surface Area
The surface area of a sphere is 4 pi r2. So, in terms of surface area of spheres:
- Area of radius 50 = area of radius 40 + area of radius 30
We don't often have spheres lying around, but boat hulls may have the same relationship (they're like deformed spheres, right?). Assuming the boats are similarly shaped, the paint needed to coat one 50 foot yacht could instead paint a 40 and 30-footer. Yowza.
Physics
If you remember your old physics classes, the kinetic energy of an object with mass m and velocity v is 1/2 m v2. In terms of energy,
- Energy at 500 mph = Energy at 400 mph + Energy at 300 mph
With the energy used to accelerate one bullet to 500 mph, we could accelerate two others to 400 and 300 mph.
Try Any Number
You can use any set of numbers that make a right triangle. For example, enter a total amount (50) and one subportion (30), and the remainder will appear below:
Suppose you want to see if a large pizza (16 inches) is bigger than two mediums (12 inches). Plug in 16 for C, and 12 for A. It looks like the large pizza can be split into a 12-inch and 10.5-inch pizza, so two-mediums are in fact bigger.
Enjoy Your New Insight
Throughout our school life we think the Pythagorean Theorem is about triangles and geometry. It's not.
When you see a right triangle, realize the sides can represent the lengths of any portion of a shape, and the sides can represent variables in any equation that has a square. Maybe it's just me, but I find this pretty surprising.
There's much, much more to this beautiful theorem, such as measuring any distance. Enjoy.
