How To Measure Any Distance With The Pythagorean Theorem

We’ve underestimated the Pythagorean theorem all along. It’s not about triangles; it can apply to any shape. It’s not about a, b and c; it applies to any formula with a squared term.

It’s not about distance in the sense of walking diagonally across a room. It’s about any distance, like the “distance” between our movie preferences or colors.

If it can be measured, it can be compared with the Pythagorean Theorem. Let’s see why.

Understanding The Theorem

We agree the theorem works. In any right triangle:

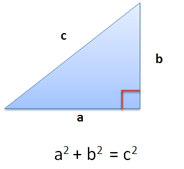
If a=3 and b=4, then c=5. Easy, right?

Well, a key observation is that a and b are at right angles (notice the little red box). Movement in one direction has no impact on the other.

It’s a bit like North/South vs. East/West. Moving North does not change your East/West direction, and vice-versa — the directions are independent (the geek term is orthogonal).

The Pythagorean Theorem lets you use find the shortest path distance between orthogonal directions. So it’s not really about right triangles — it’s about comparing “things” moving at right angles.

You: If I walk 3 blocks East and 4 blocks North, how far am I from my starting point?

Me: 5 blocks, as the crow flies. Be sure to bring adequate provisions for your journey.

You: Uh, ok.

So what is “c”?

Well, we could think of c as just a number, but that keeps us in boring triangle-land. I like to think of c as a combination of a and b.

But it’s not a simple combination like addition — after all, c doesn’t equal a + b. It’s more a combination of components — the Pythagorean theorem lets us combine orthogonal components in a manner similar to addition. And there’s the magic.

In our example, C is 5 blocks of “distance”. But it’s more than that: it contains a combination of 3 blocks East and 4 blocks North. Moving along C means you go East and North at the same time. Neat way to think about it, eh?

Chaining the Theorem

Let’s get crazy and chain the theorem together. Take a look at this:

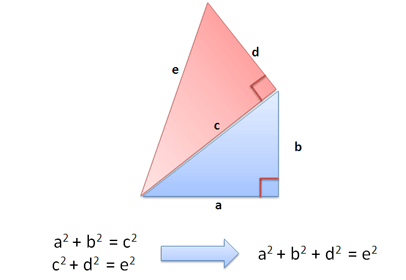
Cool, eh? We draw another triangle in red, using c as one of the sides. Since c and d are at right angles (orthogonal!), we get the Pythagorean relation: c² + d² = e².

And when we replace c² with a² + b² we get:

$\displaystyle{a^2 + b^2 + d^2 = e^2}$

And that’s something: We’ve written e in terms of 3 orthogonal components (a, b and d). Starting to see a pattern?

Put on your 3D Goggles

Think two triangles are strange? Try pulling one out of the paper. Instead of lining the triangles flat, tilt the red one up:

It’s the same triangle, just facing a different way. But now we’re in 3d! If we call the sides x, y and z instead of a, b and d we get:

$\displaystyle{x^2 + y^2 + z^2 = \text{distance}^2}$

Very nice. In math we typically measure the x-coordinate [left/right distance], the y-coordinate [front-back distance], and the z-coordinate [up/down distance]. And now we can find the 3-d distance to a point given its coordinates!

Use Any Number of Dimensions

As you can guess, the Pythagorean Theorem generalizes to any number of dimensions. That is, you can chain a bunch of triangles together and tally up the “outside” sections:

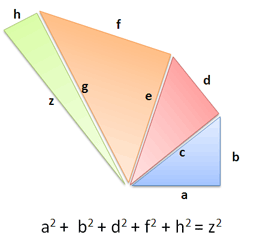
You can imagine that each triangle is in its own dimension. If segments are at right angles, the theorem holds and the math works out.

How Distance Is Computed

The Pythagorean Theorem is the basis for computing distance between two points. Consider two triangles:

Triangle with sides (4,3) [blue]
Triangle with sides (8,5) [pink]

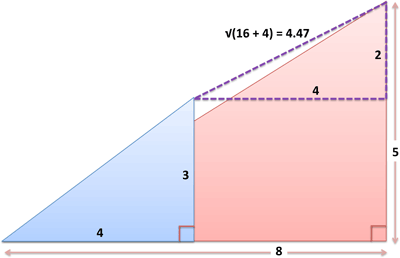
What’s the distance from the tip of the blue triangle [at coordinates (4,3)] to the tip of the red triangle [at coordinates (8,5)]? Well, we can create a virtual triangle between the endpoints by subtracting corresponding sides. The hypotenuse of the virtual triangle is the distance between points:

Distance: $(8-4, 5-3) = (4,2) = \sqrt{4^2 + 2^2} = \sqrt{20} = 4.47$

Cool, eh? In 3D, we can find the distance between points $(x_1,y_1,z_1)$ and $(x_2,y_2,z_2)$ using the same approach:

$\displaystyle{\text{distance}^2 = (x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2}$

And it doesn’t matter if one side is bigger than the other, since the difference is squared and will be positive (another great side-effect of the theorem).

How to Use Any Distance

The theorem isn’t limited to our narrow, spatial definition of distance. It can apply to any orthogonal dimensions: space, time, movie tastes, colors, temperatures. In fact, it can apply to any set of numbers (a,b,c,d,e). Let’s take a look.

Measuring User Preferences

Let’s say you do a survey to find movie preferences:

How did you like Rambo? (1-10)
How did you like Bambi? (1-10)
How did you like Seinfeld? (1-10)

How do we compare people’s ratings? Find similar preferences? Pythagoras to the rescue!

If we represent ratings as a "point" (Rambo, Bambi, Seinfeld) we can represent our survey responses like this:

Tough Guy: (10, 1, 3)
Average Joe: (5, 5, 5)
Sensitive Guy: (1, 10, 7)

And using the theorem, we can see how different people are:

Tough Guy to Average Joe: $(10 – 5, 1 – 5, 3 – 5) = (5, -4, -2) = \sqrt{(5)^2 + (-4)^2 + (-2)^2} = \sqrt{45} = 6.7$
Tough Guy to Sensitive Guy: $(10 – 1, 1 – 10, 3 – 7) = (9, -9, -4) = \sqrt{(9)^2 + (-9)^2 + (-4)^2} = \sqrt{178} = 13.34$

We can compute the results using a² + b² + c² = distance² version of the theorem. As we suspected, there’s a large gap between the Tough and Sensitive Guy, with Average Joe in the middle. The theorem helps us quantify this distance and do interesting things like cluster similar results.

This technique can be used to rate Netflix movie preferences and other types of collaborative filtering where you attempt to make predictions based on preferences (i.e. Amazon recommendations). In geek speak, we represented preferences as a vector, and use the theorem to find the distance between them (and group similar items, perhaps).

Finding Color Distance

Measuring “distance” between colors is another useful application. Colors are represented as red/green/blue (RGB) values from 0(min) to 255 (max). For example

Black: (0, 0, 0) — no colors
White: (255, 255, 255) — maximum of each color
Red: (255, 0, 0) — pure red, no other colors

We can map out all colors in a “color space”, like so:

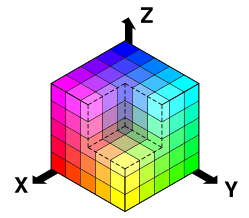
We can get distance between colors the usual way: get the distance from our (red, green, blue) value to black (0,0,0) [formally labeled delta e]. It appears humans can’t tell the difference between colors only 4 units apart; heck, even 30 units looks pretty close to me:

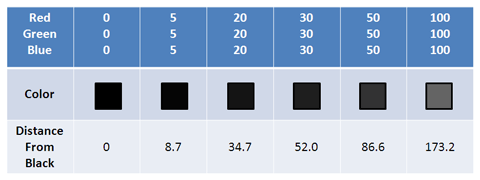
How similar do these look to you? The color distance gives us a quantifiable way to measure the distance between colors (try for yourself). You can even unscramble certain blurred images by cleverly applying color distance.

The Point: You can measure anything

If you can represent a set of characteristics with numbers, you can compare them with the theorem:

Temperatures during the week: (Mon, Tues, Wed, Thurs, Fri). Compare successive weeks to see how “different” they are (find the difference between 5-dimensional vectors).
Number of customers coming into a store hour-by-hour, day-by-day, or week-by-week
SpaceTime distance: (latitude, longitude, altitude, date). Useful if you’re making a time machine (or a video game that uses one)!
Differences between people: (Height, Weight, Age)
Differences between companies: (Revenue, Profit, Market Cap)

You can tweak the distance by weighing traits differently (i.e., multiplying the age difference by a certain factor). But the core idea is so important I’ll repeat it again: if you can quantify it, you can compare it using the the Pythagorean Theorem.

Your x, y and z axes can represent any quantity. And you aren’t limited to 3 dimensions. Sure, mathematicians would love to tell you about the other ways to measure distance (aka metric space), but the Pythagorean Theorem is the most famous and a great starting point.

So, What Just Happened Here?

There’s so much to learn when revisiting concepts we were “taught”. Math is beautiful, but the elegance is usually buried under mechanical proofs and a wall of equations. We don’t need more proofs; we need interesting, intuitive results.

For example, the Pythagorean Theorem:

Works for any shape, not just triangles (like circles)
Works for any equation with squares (like 1/2 m v²)
Generalizes to any number of dimensions (a² + b² + c² + …)
Measures any type of distance (i.e. between colors or movie preferences)

Not too bad for a 2000-year old result, right? This is quite a brainful, so I’ll finish here for today (the previous article has more uses). Happy math.