Trig mnemonics like SOH-CAH-TOA focus on computations, not concepts:
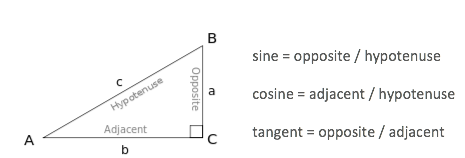
TOA explains the tangent about as well as $x^2 + y^2 = r^2$ describes a circle. Sure, if you’re a math robot, an equation is enough. The rest of us, with organic brains half-dedicated to vision processing, seem to enjoy imagery. And “TOA” evokes the stunning beauty of an abstract ratio.
I think you deserve better, and here’s what made trig click for me.
- Visualize a dome, a wall, and a ceiling
- Trig functions are percentages to the three shapes
Motivation: Trig Is Anatomy
Imagine Bob The Alien visits Earth to study our species.
Without new words, humans are hard to describe: “There’s a sphere at the top, which gets scratched occasionally” or “Two elongated cylinders appear to provide locomotion”.
After creating specific terms for anatomy, Bob might jot down typical body proportions:
- The armspan (fingertip to fingertip) is approximately the height
- A head is 5 eye-widths wide
- Adults are 8 head-heights tall
How is this helpful?
Well, when Bob finds a jacket, he can pick it up, stretch out the arms, and estimate the owner’s height. And head size. And eye width. One fact is linked to a variety of conclusions.
Even better, human biology explains human thinking. Tables have legs, organizations have heads, crime bosses have muscle. Our biology offers ready-made analogies that appear in man-made creations.
Now the plot twist: you are Bob the alien, studying creatures in math-land!
Generic words like “triangle” aren’t overly useful. But labeling sine, cosine, and hypotenuse helps us notice deeper connections. And scholars might study haversine, exsecant and gamsin, like biologists who find a link between your tibia and clavicle.
And because triangles show up in circles…
…and circles appear in cycles, our triangle terminology helps describe repeating patterns!
Trig is the anatomy book for “math-made” objects. If we can find a metaphorical triangle, we’ll get an armada of conclusions for free.
Sine/Cosine: The Dome
Instead of staring at triangles by themselves, like a caveman frozen in ice, imagine them in a scenario, hunting that mammoth.
Pretend you’re in the middle of your dome, about to hang up a movie screen. You point to some angle “x”, and that’s where the screen will hang.
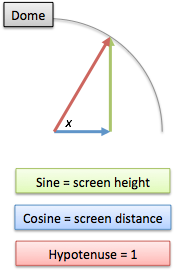
The angle you point at determines:
- sine(x) = sin(x) = height of the screen, hanging like a sign
- cosine(x) = cos(x) = distance to the screen along the ground [“cos” ~ how “close”]
- the hypotenuse, the distance to the top of the screen, is always the same
Want the biggest screen possible? Point straight up. It’s at the center, on top of your head, but it’s big dagnabbit.
Want the screen the furthest away? Sure. Point straight across, 0 degrees. The screen has “0 height” at this position, and it’s far away, like you asked.
The height and distance move in opposite directions: bring the screen closer, and it gets taller.
Tip: Trig Values Are Percentages
Nobody ever told me in my years of schooling: sine and cosine are percentages. They vary from +100% to 0 to -100%, or max positive to nothing to max negative.
Let’s say I paid \$14 in tax. You have no idea if that’s expensive. But if I say I paid 95% in tax, you know I’m getting ripped off.
An absolute height isn’t helpful, but if your sine value is .95, I know you’re almost at the top of your dome. Pretty soon you’ll hit the max, then start coming down again.
How do we compute the percentage? Simple: divide the current value by the maximum possible (the radius of the dome, aka the hypotenuse).
That’s why we’re told “Sine = Opposite / Hypotenuse”. It’s to get a percentage! A better wording is “Sine is your height, as a percentage of the hypotenuse”. (Sine becomes negative if your angle points “underground”. Cosine becomes negative when your angle points backwards.)
Let’s simplify the calculation by assuming we’re on the unit circle (radius 1). Now we can skip the division by 1 and just say sine = height.
Every circle is really the unit circle, scaled up or down to a different size. So work out the connections on the unit circle and apply the results to your particular scenario.
Try it out: plug in an angle and see what percent of the height and width it reaches:
The growth pattern of sine isn’t an even line. The first 45 degrees cover 70% of the height, and the final 10 degrees (from 80 to 90) only cover 2%.
This should make sense: at 0 degrees, you’re moving nearly vertical, but as you get to the top of the dome, your height changes level off.
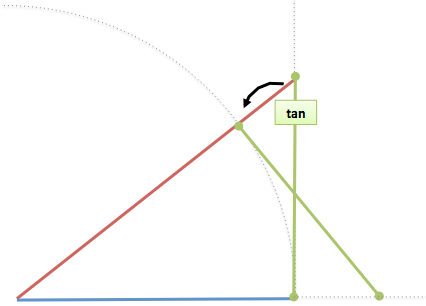
Tangent/Secant: The Wall
One day your neighbor puts up a wall right next to your dome. Ack, your view! Your resale value!
But can we make the best of a bad situation?
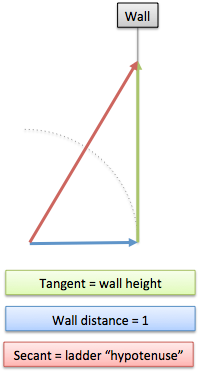
Sure. What if we hang our movie screen on the wall? You point at an angle (x) and figure out:
- tangent(x) = tan(x) = height of screen on the wall
- distance to screen: 1 (the screen is always the same distance along the ground, right?)
- secant(x) = sec(x) = the “ladder distance” to the screen
We have some fancy new vocab terms. Imagine seeing the Vitruvian “TAN GENTleman” projected on the wall. You climb the ladder, making sure you can “SEE, CAN’T you?”. (Yeah, he’s naked… won’t forget the analogy now, will you?)
Let’s notice a few things about tangent, the height of the screen.
It starts at 0, and goes infinitely high. You can keep pointing higher and higher on the wall, to get an infinitely large screen! (That’ll cost ya.)
Tangent is just a bigger version of sine! It’s never smaller, and while sine “tops off” as the dome curves in, tangent keeps growing.
How about secant, the ladder distance?
- Secant starts at 1 (ladder on the floor to the wall) and grows from there
- Secant is always longer than tangent. The leaning ladder used to put up the screen must be longer than the screen itself, right? (At enormous sizes, when the ladder is nearly vertical, they’re close. But secant is always a smidge longer.)
Remember, the values are percentages. If you’re pointing at a 50-degree angle, tan(50) = 1.19. Your screen is 19% larger than the distance to the wall (the radius of the dome).
(Plug in x=0 and check your intuition that tan(0) = 0, and sec(0) = 1.)
Cotangent/Cosecant: The Ceiling
Amazingly enough, your neighbor now decides to build a ceiling on top of your dome, far into the horizon. (What’s with this guy? Oh, the naked-man-on-my-wall incident…)
Well, time to build a ramp to the ceiling, and have a little chit chat. You pick an angle to build and work out:
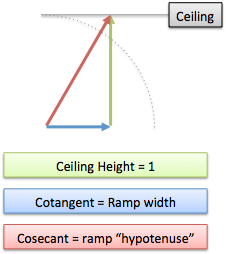
- cotangent(x) = cot(x) = how far the ceiling extends before we connect
- cosecant(x) = csc(x) = how long we walk on the ramp
- the vertical distance traversed is always 1
Tangent/secant describe the wall, and COtangent and COsecant describe the ceiling.
Our intuitive facts are similar:
- If you pick an angle of 0, your ramp is flat (infinite) and never reachers the ceiling. Bummer.
- The shortest “ramp” is when you point 90-degrees straight up. The cotangent is 0 (we didn’t move along the ceiling) and the cosecant is 1 (the “ramp length” is at the minimum).
Visualize The Connections
A short time ago I had zero “intuitive conclusions” about the cosecant. But with the dome/wall/ceiling metaphor, here’s what we see:
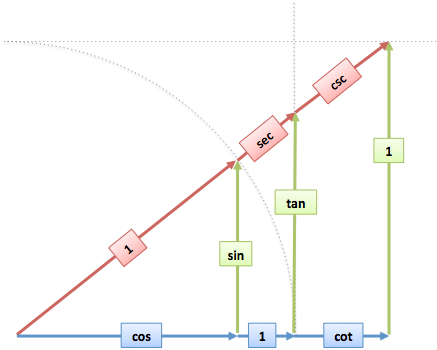
Whoa, it’s the same triangle, just scaled to reach the wall and ceiling. We have vertical parts (sine, tangent), horizontal parts (cosine, cotangent), and “hypotenuses” (secant, cosecant). (Note: the labels show where each item “goes up to”. Cosecant is the full distance from you to the ceiling.)
Now the magic. The triangles have similar facts:
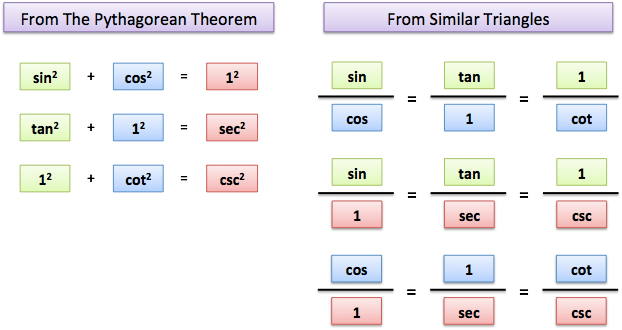
From the Pythagorean Theorem ($a^2 + b^2 = c^2$) we see how the sides of each triangle are linked.
And from similarity, ratios like “height to width” must be the same for these triangles. (Intuition: step away from a big triangle. Now it looks smaller in your field of view, but the internal ratios couldn’t have changed.)
This is how we find out “sine/cosine = tangent/1”.
I’d always tried to memorize these facts, when they just jump out at us when visualized. SOH-CAH-TOA is a nice shortcut, but get a real understanding first!
Gotcha: Remember Other Angles
Psst… don’t over-focus on a single diagram, thinking tangent is always smaller than 1. If we increase the angle, we reach the ceiling before the wall:
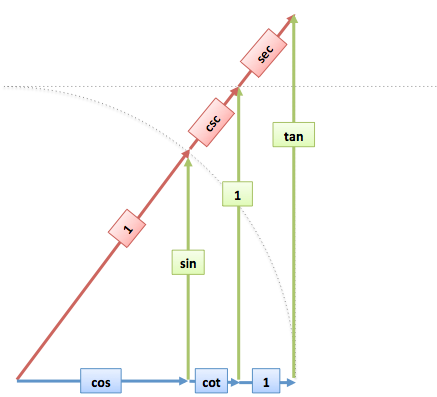
The Pythagorean/similarity connections are always true, but the relative sizes can vary.
(But, you might notice that sine and cosine are always smallest, or tied, since they’re trapped inside the dome. Nice!)
Summary: What Should We Remember?
For most of us, I’d say this is enough:
- Trig explains the anatomy of “math-made” objects, such as circles and repeating cycles
- The dome/wall/ceiling analogy shows the connections between the trig functions
- Trig functions return percentages, that we apply to our specific scenario
You don’t need to memorize $1^2 + \cot^2 = \csc^2$, except for silly tests that mistake trivia for understanding. In that case, take a minute to draw the dome/wall/ceiling diagram, fill in the labels (a tan gentleman you can see, can’t you?), and create a cheatsheet for yourself.
In a follow-up, we’ll learn about graphing, complements, and using Euler’s Formula to find even more connections.
Appendix: The Original Definition Of Tangent
You may see tangent defined as the length of the tangent line from the circle to the x-axis (geometry buffs can work this out).
As expected, at the top of the circle (x=90) the tangent line can never reach the x-axis and is infinitely long.
I like this intuition because it helps us remember the name “tangent”, and here’s a nice interactive trig guide to explore:
Still, it’s critical to put the tangent vertical and recognize it’s just sine projected on the back wall (along with the other triangle connections).
Appendix: Inverse Functions
Trig functions take an angle and return a percentage. $\sin(30) = .5$ means a 30-degree angle is 50% of the max height.
The inverse trig functions let us work backwards, and are written $\sin^{-1}$ or $\arcsin$ (“arcsine”), and often written asin in various programming languages.
If our height is 25% of the dome, what’s our angle?
Plugging asin(.25) into a calculator gives an angle of 14.5 degrees.
Now what about something exotic, like inverse secant? Often times it’s not available as a calculator function (even the one I built, sigh).
Looking at our trig cheatsheet, we find an easy ratio where we can compare secant to 1. For example, secant to 1 (hypotenuse to horizontal) is the same as 1 to cosine:
![]()
Suppose our secant is 3.5, i.e. 350% of the radius of the unit circle. What’s the angle to the wall?
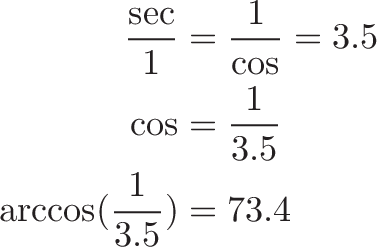
Appendix: A Few Examples
Example: Find the sine of angle x.
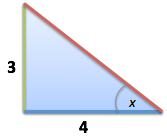
Ack, what a boring question. Instead of “find the sine” think, “What’s the height as a percentage of the max (the hypotenuse)?”.
First, notice the triangle is “backwards”. That’s ok. It still has a height, in green.
What’s the max height? By the Pythagorean theorem, we know
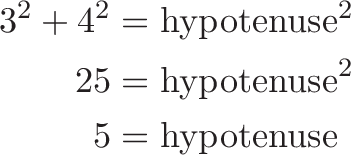
Ok! The sine is the height as a percentage of the max, which is 3/5 or .60.
Follow-up: Find the angle.
Of course. We have a few ways. Now that we know sine = .60, we can just do:
![]()
Here’s another approach. Instead of using sine, notice the triangle is “up against the wall”, so tangent is an option. The height is 3, the distance to the wall is 4, so the tangent height is 3/4 or 75%. We can use arctangent to turn the percentage back into an angle:
![]()
![]()
Example: Can you make it to shore?
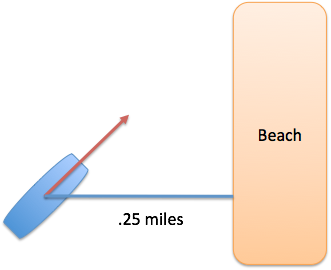
You’re on a boat with enough fuel to sail 2 miles. You’re currently .25 miles from shore. What’s the largest angle you could use and still reach land? Also, the only reference available is Hubert’s Compendium of Arccosines, 3rd Ed. (Truly, a hellish voyage.)
Ok. Here, we can visualize the beach as the “wall” and the “ladder distance” to the wall is the secant.
First, we need to normalize everything in terms of percentages. We have 2 / .25 = 8 “hypotenuse units” worth of fuel. So, the largest secant we could allow is 8 times the distance to the wall.
We’d like to ask “What angle has a secant of 8?”. But we can’t, since we only have a book of arccosines.
We use our cheatsheet diagram to relate secant to cosine: Ah, I see that “sec/1 = 1/cos”, so
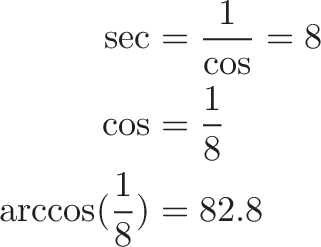
A secant of 8 implies a cosine of 1/8. The angle with a cosine of 1/8 is arccos(1/8) = 82.8 degrees, the largest we can afford.
Not too bad, right? Before the dome/wall/ceiling analogy, I’d be drowning in a mess of computations. Visualizing the scenario makes it simple, even fun, to see which trig buddy can help us out.
In your problem, think: am I interested in the dome (sin/cos), the wall (tan/sec), or the ceiling (cot/csc)?
Happy math.
Update: The owner of Grey Matters put together interactive diagrams for the analogies (drag the slider on the left to change the angle):
- Sine/Cosine: The Dome
- Tangent/Secant: The Wall
- Cotangent/Cosecant: The Ceiling
- Combined visualization
Thanks!
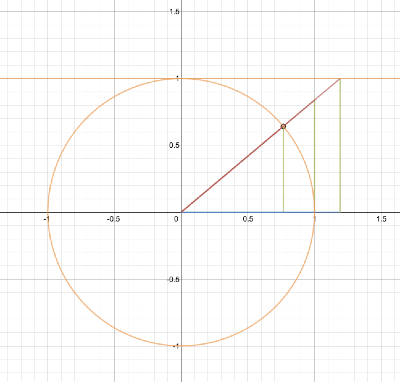
.png)
.png)