Let's say you had to estimate 1 + 2 + 3 + 4 + 5 + 6 + 7 + ... + 100.

What would you do? Well, you could work out the exact formula:

\displaystyle{\frac{(n + 1)(n)}{2}}

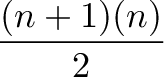
and plug in n=100 to get 5050.

But we just want a rough answer. You have a list of numbers, they follow a simple pattern, and want a quick estimate. What to do?

The "easy" way (well, the Calculus way) is to realize 1 + 2 + 3 + 4 is about the same as f(x) = x. The first element is f(1) = 1, the second is f(2) = 2, and so on.

From here, we can take the integral:

\displaystyle{ \int x = \frac{1}{2} x^2 }

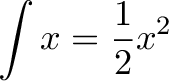
We usually see the integral as a formal, elegant operation, which artfully accumulates one function and returns another. Informally, we're squashing everything together in that bad mamma-jamma and seeing how much there is.

The result frac(1)(2) x2 should be pretty close to what we want.

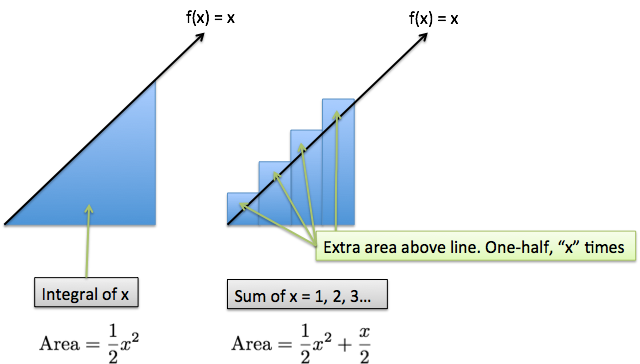
calculus-sum-x

The exact total is our staircase-like pattern, which accumulates to 5050.

The approximate answer is the area of that triangle, frac(1)(2) base · height = frac(1)(2) 100 · 100 = 5000. The difference is because of the corners in the staircase which overhang. frac(x)(2) is one-half, x times (the size of overhang (1/2) times the number of pieces (x)).

The net result is using a smooth, easy-to-measure shape to approximate a jagged, tedious-to-measure one. (This is a bit of Calculus inception, since we usually use rectangles to approximate smooth shapes.)

More Estimates

This tactic works for other sequences:

What's the sum of the first 10 square numbers? 1 + 4 + 9 + 16 + 25 + ... + 100 = ?

Hrm. The formula is probably tricky to work out. But without our Calculus-infused Arithmetic, a quick guess would be:

\displaystyle{\int x^2 = \frac{1}{3} x^3}

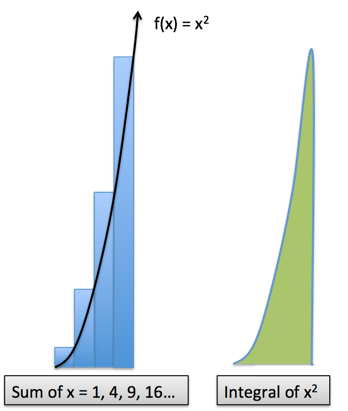
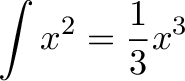
Our first hunch should be "one third of 10^3" or 333. But as we saw before, there's an "overhang" that we missed. Let's call it 10%, for an estimate of 330 + 10% ~ 370.

The exact answer is 385. Not bad! The actual formula is:

\displaystyle{P_{n}=\sum _{k=1}^{n}k^{2}={\frac {n(n+1)(2n+1)}{6}}={\frac {2n^{3}+3n^{2}+n}{6}}={\frac {n^{3}}{3}}+{\frac {n^{2}}{2}}+{\frac {n}{6}} }

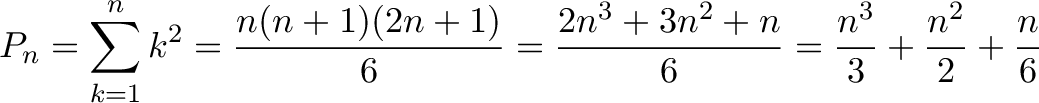
I'd say frac(x3)(3) isn't bad for a few seconds of work.

Data doubles every year. What does lifetime usage look like?

The integral (squashed-together total) of an exponential is an exponential. In Calculus terms,

\displaystyle{\int e^x = e^x}

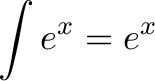
The key insight is that all exponential growth is just a variation of ex. If ex accumulates exponentially, so will 2x.

So the total usage to date will also follow an exponential pattern, doubling every year also. Contrast this with a usage pattern of "1 + 2 + 3 + 4 ..." -- we grow linearly (f(x) = x), but total usage accumulates quadratically (frac(1)(2)x2).

My goal is to incorporate math thinking into everyday scenarios. We start with an arithmetic question, convert it to a geometry puzzle (how big is the staircase?), and then use calculus to approximate it.

I know a concept is clicking when I can switch between a few styles of thought. Imagine the problem as a script: how would Spielberg, Tarantino, or Scorsese direct it? Each field takes a different look. (To learn how to think with Calculus, check out the Calculus Guide.)

Happy math.

{{ strings.title }}

{{item.title}}
{{item.text }}
 Show {{ filteredItems.length - limit }} more