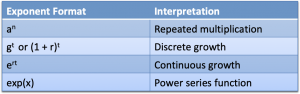
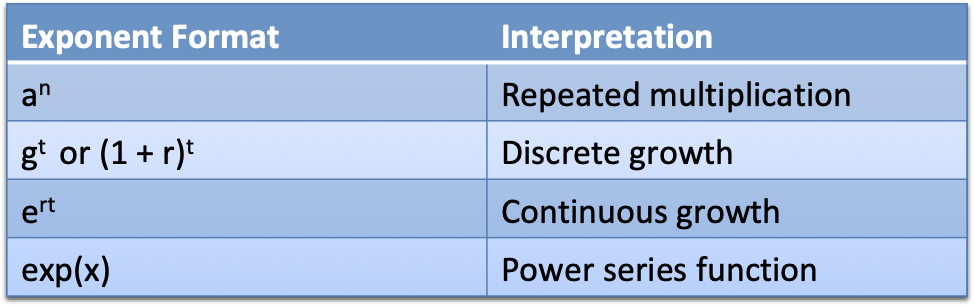
BetterExplained » What does an exponent really mean?

Ever get a hint of confusion about what an exponent was doing? I sure have.

Like the word "run", the meaning depends on context:

crawl / walk / run (movement)
run a company (general operation)
a run of good luck (sequence)
and a dozen more definitions

Sticking with a single interpretation of "run" leads to confusion, and the same happens in math. Let's clarify how exponents are used.

What does an exponent really mean?

Meaning 1: Repeated Multiplication

We first learn that exponents like $3^2$ or $a^n$ are repeated multiplication: multiply $a$, $n$ times.

Like counting on your fingers, this breaks down beyond the positive integers. What does a fractional exponent mean? A negative one? Zero? (Since $a^0 = 1$, we multiply zero times and get 1?)

Common usage of $a^n$: Counting problems. If you flip a coin $n$ times, you have $2^n$ possible outcomes.

Meaning 2: Growth Microwave

Let's say I have an exponent like $3^{4.5}$. I mentally convert it to $1.0 * 3^{4.5}$, and then $1.0 * g^{t}$.

With the "growth microwave" analogy, an exponent grows our starting amount (1.0) by $g$ for $t$ units of time. (In this example, 3x growth applied for for 4.5 seconds.)

What values can $t$ have?

If t is positive, we go forward in time and get larger (assuming $g > 1$). Fractional time is ok -- I can run a microwave for 3.5 minutes, and get some effect between 3 minutes and 4 minutes.
If t is negative, we go backwards in time and get smaller. If a regular microwave allowed negative time, it would cool down your food, right?
If t is zero, we didn't use the machine at all! We're left with 1.0, our original amount.

The growth microwave interpretation helps with fractional powers (and resolves the t=0 issue), but it's not flexible. Doubling the rate and halving the time doesn't have the result we expect:

$\displaystyle{3^2 \neq 6^1}$

2 seconds of 3x growth isn't the same as 1 second of 6x growth. Ugh. I'm not a caveman, we need to mix rate and time! (Hold onto that thought.)

Common usage of $g^t$: Man-made systems. If I agree to pay you 15% at a certain discrete interval (yearly), we can model the outcome as $(1.15)^t$. If I decide to cut the payments short (2.5 years) we can exponentially interpolate between the two intervals ($r^{0.5}$ is the square root). We often set $g = (1 + r)$, so we could write $(1 + .15)^t$.

Aside: Let's prove $g^t$ isn't flexible.

$\begin{aligned} g^t &\stackrel{?}{=} (gn)^{t/n} \ [\text{claim to test}] \\ g^{tn} &\stackrel{?}{=} (gn)^{t} \ [\text{raise both sides to nth power}] \\ g^{n} &\stackrel{?}{=} (gn) \ [\text{raise both sides to (1/t) power}] \\ g^{n} &\neq (gn) \ [\text{not true in general}] \end{aligned}$

However, this shows the special case of $2^2 = 4^1$ does work.

Meaning 3: Continuous Growth Engine

Regular readers know I think of e as a continuous growth engine:

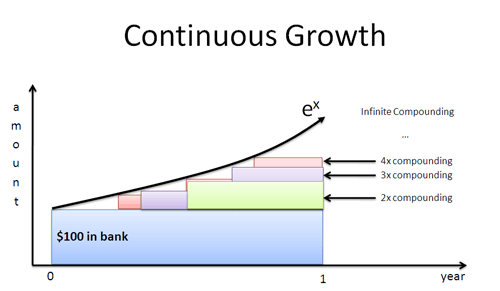
Instead of waiting to grow at discrete intervals, we apply interest immediately and compound as fast as we can. A pleasant consequence of e's definition is that we merge rate and time into a single, interchangeable quantity:

$\displaystyle{e^{50\% \cdot 2} = e^{100\% \cdot 1} = e^{r \cdot t} = e^{x}}$

Conveniently, 2 years of 50% growth is the same as 1 year of 100% growth. We doubled our rate, halved our time, and got the same result. (Practically, we may prefer the shorter time period but the final quantity is the same.)

The input $x$ is the "growth fuel" that can be separated into "rate * time". The base, e, is a machine that just cares how much fuel you gave it. Drip the fuel over 50 time periods, or firehose it into a single one. Either way, the same total input $x$ gets the same final result.

Common usage of $e^{rt}$: Natural systems. Most laws of physics have continuous growth patterns (no delay between earning interest and using it). We may occasionally use the man-made version for our convenience, e.g., describing a radioactive half life of 20 years, even though the atoms are decaying on an instant-by-instant basis.

(Aside: Use the natural log to convert one exponent format to another. $g^t = e^{\ln(g)t}$)

Meaning 4: A Power Series Calculation

We can treat $e^x$ as a fancy mathematical function:

$\displaystyle{e^x = 1 + x + \frac{x^2}{2!} + \frac{x^3}{3!} + \frac{x^4}{4!} + ...}$

You may see $e^x$ written $\exp(x)$, treated like any other function $f(x)$. Here, $x$ is just a numerical input to an intricate power series. Concepts like repeated counting, growth rate, and time fall into the background (though we can see them if we look).

Curiously, we're left with integer powers ($x^0, x^1, x^2, x^3$) and our "repeated multiplication" interpretation shows up again! The power of the exponent, $x$, switches from the number of multiplications to the base being multiplied. (The ciiiircle of life.)

Common usage of $\exp(x)$: When we see $e^x$ as just another function, a few properties emerge:

Using calculus with exponents gets way easier, since we can take the derivative / integral of each term (and realize $\frac{d}{dx} e^x = e^x$).
Exponential approximations become easy: $e^x \sim 1 + x$ for small values of $x$, since the higher-order powers become negligible.
Other math patterns click. Sine and cosine have expansions similar to $e^x$, hinting that trig functions and exponents are connected (Euler's Formula).
$e^x$ looks like a polynomial of infinite degree, and will eventually surpass any finite polynomial. (While $x^2 + 100 > e^x$ in the beginning, $e^x$ will eventually exceed it.)

So which version of exponents is best?

You probably guessed it: it depends, though the interpretations are listed from most to least common for a general audience.

If a formula doesn't make sense, try switching versions. Life's too short to have only a single interpretation of exponents.

Happy math.

Meaning 1: Repeated Multiplication

Meaning 2: Growth Microwave

Meaning 3: Continuous Growth Engine

Meaning 4: A Power Series Calculation

So which version of exponents is best?

Other Posts In This Series