- BetterExplained - https://betterexplained.com -

Using Logarithms in the Real World

Posted By kalid On In Math | 61 Comments
Using Logarithms in the Real World

Logarithms are everywhere. Ever use the following phrases?

You're describing numbers in terms of their powers of 10, a logarithm. And an interest rate is the logarithm of the growth in an investment.

Surprised that logarithms are so common? Me too. Most attempts at Math In the Real World (TM) point out logarithms in some arcane formula, or pretend we're geologists fascinated by the Richter Scale. "Scientists care about logs, and you should too. Also, can you imagine a world without zinc?"

No, no, no, no no, no no! (Mama mia!)

Math expresses concepts with notation like "ln" or "log". Finding "math in the real world" means encountering ideas in life and seeing how they could be written with notation. Don't look for the literal symbols! When was the last time you wrote a division sign? When was the last time you chopped up some food?

Ok, ok, we get it: what are logarithms about?

Logarithms find the cause for an effect, i.e the input for some output

A common "effect" is seeing something grow, like going from \$100 to \$150 in 5 years. How did this happen? We're not sure, but the logarithm finds a possible cause: A continuous return of ln(150/100) / 5 = 8.1% would account for that change. It might not be the actual cause (did all the growth happen in the final year?), but it's a smooth average we can compare to other changes.

By the way, the notion of "cause and effect" is nuanced. Why is 1000 bigger than 100?

We can think of numbers as outputs (1000 is "1000 outputs") and inputs ("How many times does 10 need to grow to make those outputs?"). So,

1000 outputs > 100 outputs

because

3 inputs > 2 inputs

Or in other words:

log(1000) > log(100)

Why is this useful?

Logarithms put numbers on a human-friendly scale.

Large numbers break our brains. Millions and trillions are "really big" even though a million seconds is 12 days and a trillion seconds is 30,000 years. It's the difference between an American vacation year and the entirety of human civilization.

The trick to overcoming "huge number blindness" is to write numbers in terms of "inputs" (i.e. their power base 10). This smaller scale (0 to 100) is much easier to grasp:

A 0 to 80 scale took us from a single item to the number of things in the universe. Not too shabby.

Logarithms count multiplication as steps

Logarithms describe changes in terms of multiplication: in the examples above, each step is 10x bigger. With the natural log, each step is "e" (2.71828...) times more.

When dealing with a series of multiplications, logarithms help "count" them, just like addition counts for us when effects are added.

Show me the math

Time for the meat: let's see where logarithms show up!

Six-figure salary or 2-digit expense

We're describing numbers in terms of their digits, i.e. how many powers of 10 they have (are they in the tens, hundreds, thousands, ten-thousands, etc.). Adding a digit means "multiplying by 10", i.e.

\displaystyle{1 \text{[1 digit]} \cdot 10 \cdot 10 \cdot 10 \cdot 10 \cdot 10 \text{[5 more digits]} = 10^5 = 100,000}

Logarithms count the number of multiplications added on, so starting with 1 (a single digit) we add 5 more digits ($10^5$) and 100,000 get a 6-figure result. Talking about "6" instead of "One hundred thousand" is the essence of logarithms. It gives a rough sense of scale without jumping into details.

Bonus question: How would you describe 500,000? Saying "6 figure" is misleading because 6-figures often implies something closer to 100,000. Would "6.5 figure" work?

Not really. In our heads, 6.5 means "halfway" between 6 and 7 figures, but that's an adder's mindset. With logarithms a ".5" means halfway in terms of multiplication, i.e the square root ($9^.5$ means the square root of 9 -- 3 is halfway in terms of multiplication because it's 1 to 3 and 3 to 9).

Taking log(500,000) we get 5.7, add 1 for the extra digit, and we can say "500,000 is a 6.7 figure number". Try it out here:

Order of magnitude

We geeks love this phrase. It means roughly "10x difference" but just sounds cooler than "1 digit larger".

In computers, where everything is counted with bits (1 or 0), each bit has a doubling effect (not 10x). So going from 8 to 16 bits is "8 orders of magnitude" or $2^8 = 256$ times larger. ("Larger" in this case refers to the amount of memory that can be addressed.) Going from 16 to 32 bits means an extra 16 orders of magnitude, or $2^16$ ~ 65,536 times more memory that can be addressed.

Interest Rates

How do we figure out growth rates? A country doesn't intend to grow at 8.56% per year. You look at the GDP one year and the GDP the next, and take the logarithm to find the implicit growth rate.

My two favorite interpretations of the natural logarithm (ln(x)), i.e. the natural log of 1.5:

Logarithms are how we figure out how fast we're growing.

Measurement Scale: Google PageRank

Google gives every page on the web a score (PageRank) which is a rough measure of authority / importance. This is a logarithmic scale, which in my head means "PageRank counts the number of digits in your score".

So, a site with pagerank 2 ("2 digits") is 10x more popular than a PageRank 1 site. My site is PageRank 5 and CNN has PageRank 9, so there's a difference of 4 orders of magnitude ($10^4$ = 10,000).

Roughly speaking, I get about 7000 visits / day. Using my envelope math, I can guess CNN gets about 7000 * 10,000 = 70 million visits / day. (How'd I do that? In my head, I think $7k * 10k = 70 * k * k = 70 * M$). They might have a few times more than that (100M, 200M) but probably not up to 700M.

Google conveys a lot of information with a very rough scale (1-10).

Measurement Scale: Richter, Decibel, etc.

Sigh. We're at the typical "logarithms in the real world" example: Richter scale and Decibel. The idea is to put events which can vary drastically (earthquakes) on a single scale with a small range (typically 1 to 10). Just like PageRank, each 1-point increase is a 10x improvement in power. The largest human-recorded earthquake was 9.5; the Yucatán Peninsula impact, which likely made the dinosaurs extinct, was 13.

Decibels are similar, though it can be negative. Sounds can go from intensely quiet (pindrop) to extremely loud (airplane) and our brains can process it all. In reality, the sound of an airplane's engine is millions (billions, trillions) of times more powerful than a pindrop, and it's inconvenient to have a scale that goes from 1 to a gazillion. Logs keep everything on a reasonable scale.

Logarithmic Graphs

You'll often see items plotted on a "log scale". In my head, this means one side is counting "number of digits" or "number of multiplications", not the value itself. Again, this helps show wildly varying events on a single scale (going from 1 to 10, not 1 to billions).

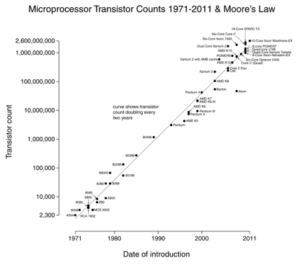
Moore's law is a great example: we double the number of transistors every 18 months (image courtesy Wikipedia).

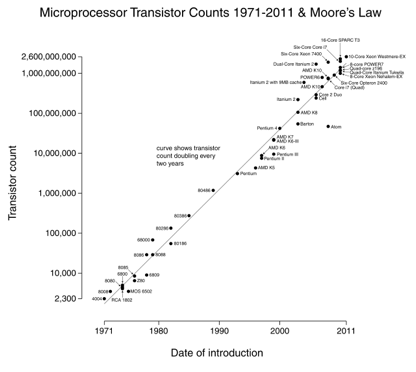
Moore's Law

The neat thing about log-scale graphs is exponential changes (processor speed) appear as a straight line. Growing 10x per year means you're steadily marching up the "digits" scale.

Onward and upward

If a concept is well-known but not well-loved, it means we need to build our intuition. Find the analogies that work, and don't settle for the slop a textbook will trot out. In my head:

Happy math.

Other Posts In This Series

  1. An Intuitive Guide To Exponential Functions & e
  2. Demystifying the Natural Logarithm (ln)
  3. A Visual Guide to Simple, Compound and Continuous Interest Rates
  4. Common Definitions of e (Colorized)
  5. Understanding Exponents (Why does 0^0 = 1?)
  6. Using Logarithms in the Real World
  7. How To Think With Exponents And Logarithms
  8. Understanding Discrete vs. Continuous Growth
  9. What does an exponent really mean?
  10. Q: Why is e special? (2.718..., not 2, 3.7 or another number?)