Quick confession? I never fully learned the trig derivatives. Sure, I memorized $\sin' = \cos$ and $\cos' = -\sin $ like everyone else, but the derivative of tangent? Cosecant? Forget it, magic spells.
After years of searching, there's a middle ground between tedious derivation and rote memorization. Aha moment: all trig functions change using the same process: (sign)(scale)(swapped function).
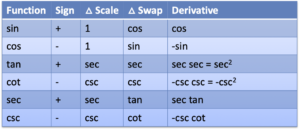
Here's the Table of Trig Derivatives we'll learn to fill out:
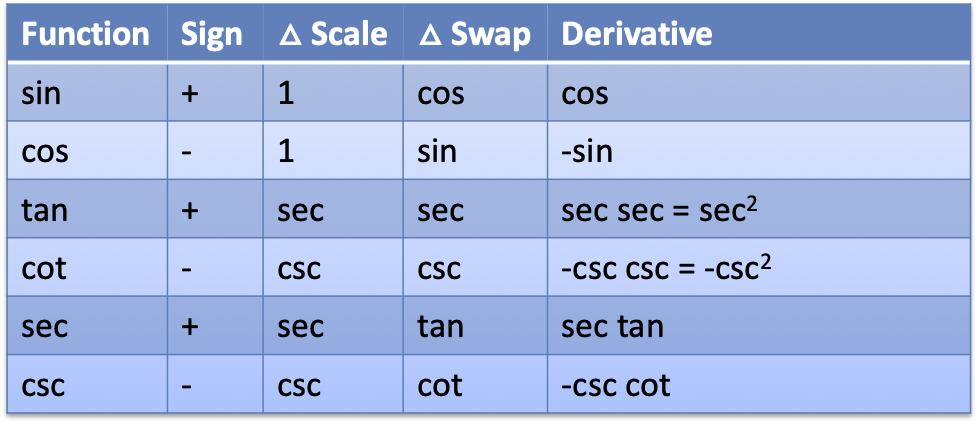
As background, learn to visualize the trig functions, and how they're related by the Pythagorean Theorem and similarity:
Part 1: Learn the table
First, let's learn to make the table, one column at a time:
- Function: The function to derive (sin, cos, tan, cot, sec, csc)
- Sign: The "primary" functions are positive, and the "co" (complementary) functions are negative
- Scale: The hypotenuse (red) used by each function
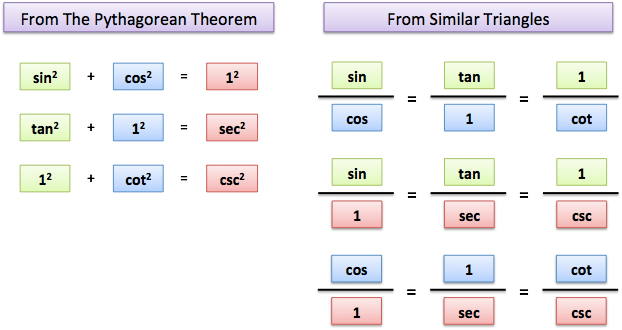
- Swap: The other function in each Pythagorean triangle (sin ⇄ cos, tan ⇄ sec, cot ⇄ csc)
- Derivative: Multiply to find the derivative
Tada! This procedure somehow finds derivatives for trig fucntions. Learning tips:
- Think "triple S": sign, scale, swap
- You've likely memorized $\sin' = \cos$ and $\cos' = -\sin$. Fill in those rows to kickstart the process.
Normally, I prefer insight to memorization. But practically, you're asking about trig derivatives because you have a test, and I want to help you now.
Like a multiplication table, after filling in the entries, we notice patterns. Could $\sin' = \cos$ and $\csc' = -\csc \cot$ have something in common?
You bet.
Part 2: Visualize the derivatives
What's the derivative of sine?
The formal approach is to plug $\sin(x)$ into the definition of derivative, do the algebra, and see that $\cos(x)$ pops out. Accurate, but unsatisfying. If $\sec(x)$ was the derivative, would you notice something was amiss? Probably not.
Here's what's happening geometrically:
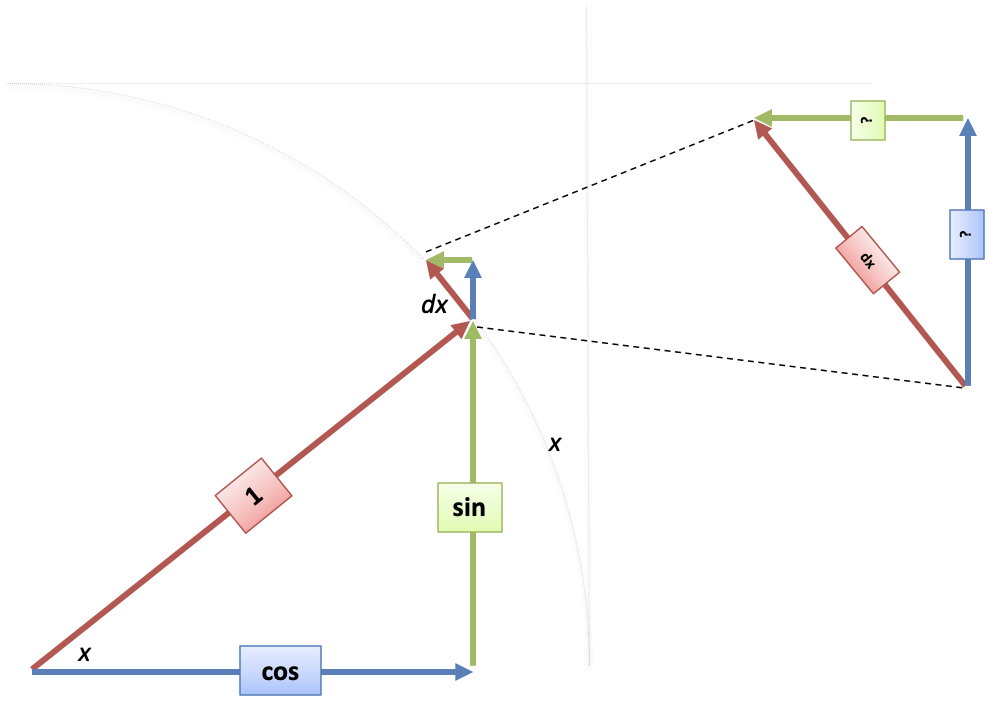
The derivative of sine means "How much does our height change when I change my angle?"
I see it like this: we have a starting angle, $x$. We increase it a smidge ($dx$), which we can place along our unit circle (since radians are distance traveled along the perimeter).
We then draw a mini-triangle based on $dx$, similar to the large one, which shows the height and width change as we move along the perimeter.
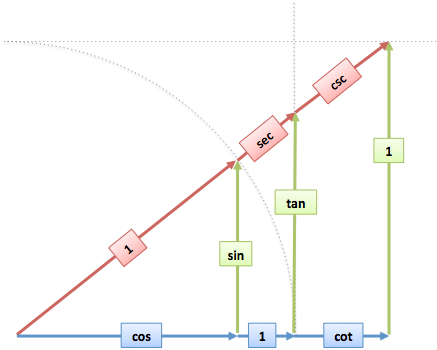
The large triangle has proportions $\text{red} : \text{blue} : \text{green} = 1 : \cos : \sin$. The mini-triangle has similar proportions, with the longest side of $dx$ instead of 1. Therefore, the mini lengths are:
$\text{mini red} : \text{mini blue} : \text{mini green} = dx : \cos dx : \sin dx$
Since mini blue is the change in sine, and mini green the change in cosine, we have:
$\sin'(x) = \text{height change} = \text{mini blue} = \cos(x) dx$
$\cos'(x) = \text{width change} = (-1) \cdot \text{mini green} = - \sin(x) dx$
Notice the negative sign with $\cos'$, since mini-green points to the left (negative).
Quick Aside: How the Columns Work
The "mini triangle" strategy works for all the trig functions. There are 3 factors:
Q1: What's the sign?
The trig co-functions are the original function applied to the complementary angle.
![]()
![]()
![]()
Just eyeballing it, we see parameters $x$ and $(90 - x)$ bandied about. The Chain Rule is whispering (screaming?) that the derivatives should be opposite, right?
Let's try it:
$\cos'(x) = [\sin(90 - x)]' = [\sin'(90 - x)][(90-x)'] = \cos(90-x)(-1)$ $= \sin(x)(-1) = -\sin(x) $
Yep, we got a negative sign.
What happened? We converted $\cos$ into its $\sin$ form (turning the angle into the complement), took the derivative, got the $-1$ term, and converted back. All the cofunctions have a similar pattern, giving us a negative sign in the table.
(Note: the negative sign means the cofunction changes opposite the original function, not that the derivative is less than zero. Cosine increases when sine is negative.)
Q2: What's the scale?
Sine and cosine live on the unit circle (radius 1). The other functions use a radius of secant (tan/sec) or cosecant (cot/csc).
Q3: What's the swapped function?
We make a mini-triangle by shrinking the original triangle down, and rotating so $dx$ matches the side of length $1$. It would be strange if, after rotation, the original colors (functions) pointed the same way.
The change must be based on the other function in the triangle (sine's change is based on cosine, cosine on sine, tangent on secant, etc.)
Also, it would be strange for a function to grow based on its own current value, right? (Hold that thought.)
Derivatives of tangent and secant
Ok, let's draw the mini triangles for tangent and secant:
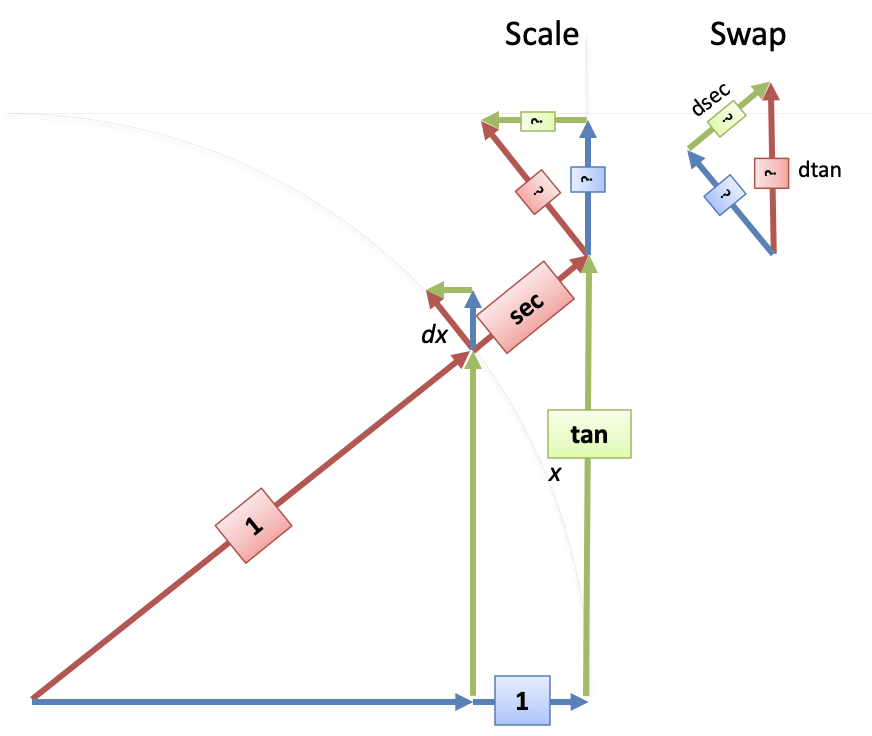
- First, we draw the $dx$ mini-triangle on the unit circle (like sin/cos).
- Next, we slide/scale the mini-triangle to fit on the "secant" radius: $dx$ becomes $\sec(x) dx$ on the secant circle.
- Last, rotate the mini-triangle so the known $1$ side (blue) matches our change of $\sec(x)dx$.
Ok. So how big are the sides of the mini triangle?
$\text{mini blue}: \text{mini green} : \text{mini red} = 1 : \tan(x) : \sec(x)$
We know $\text{mini blue} = \sec(x) dx$, so we just scale up the other sides by that amount:
- $d\sec = \text{mini green} = \tan(x) [\text{mini blue}] = \tan(x) \sec(x)dx = \sec(x) \tan(x) dx$
- $d\tan= \text{mini red} = \sec(x) [\text{mini blue}] = \sec(x) \sec(x)dx = \sec^2(x) dx$
Nice! I like how this matches the sine/cosine process. We're just measuring sides in the mini-triangle.
Derivatives of Cosecant and Cotangent
For completeness, here's csc/cot:
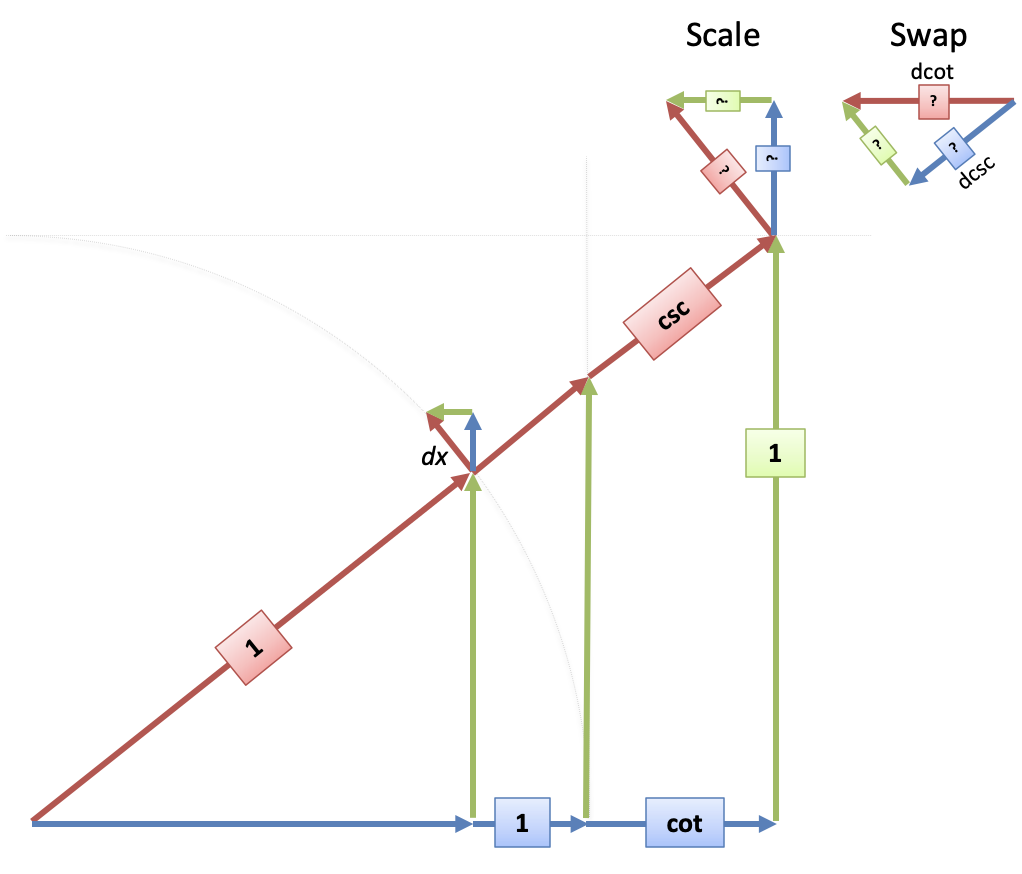
Notice how $d\cot$ and $d\csc$ in the mini-triangle move against their positive sides in the big triangle. Using the same sign, scale, swap process, we get:
$\cot' = (-)(\csc)(\csc) = -\csc^2$
$\csc' = (-)(\csc)(\cot) = -\csc \cot$
Colorizing the sides really helps me link the mini-triangle back to the original.
Now, we didn't have to draw this all out: we already know $\tan'$ and $\sec'$. Using the chain rule and complementary functions, we can do:
$\cot(x)' = [\tan(90-x)]' = \tan'(90-x)(90 - x)' = \sec^2(90-x)(-1) = -\csc^2(x)$
$\csc(x)' = [\sec(90-x)]' = \sec'(90-x)(90 - x)' = \sec(90-x)\tan(90-x)(-1)$ $= -\csc(x)\cot(x)$
Summary: What do the derivatives mean?
Blindly memorizing trig derivatives doesn't teach you much.
The deeper intuition: Trig derivatives are based on 3 effects: the sign, the radius (scale), and the other function.
So instead of $\tan' = \sec^2$, think of it as $\tan' = (+)(\sec)(\sec)$, aka $(\text{sign})(\text{scale})(\text{swapped function})$. Heck, you can even see $\cos' = (-)(1)(\sin)$.
If you can complete the derivative table and draw the mini-triangles, you'll have a much better understanding of trig than I ever did.
Happy math.
Appendix: Combined Diagram
It's a bit busy, but here's all the mini-triangles together:
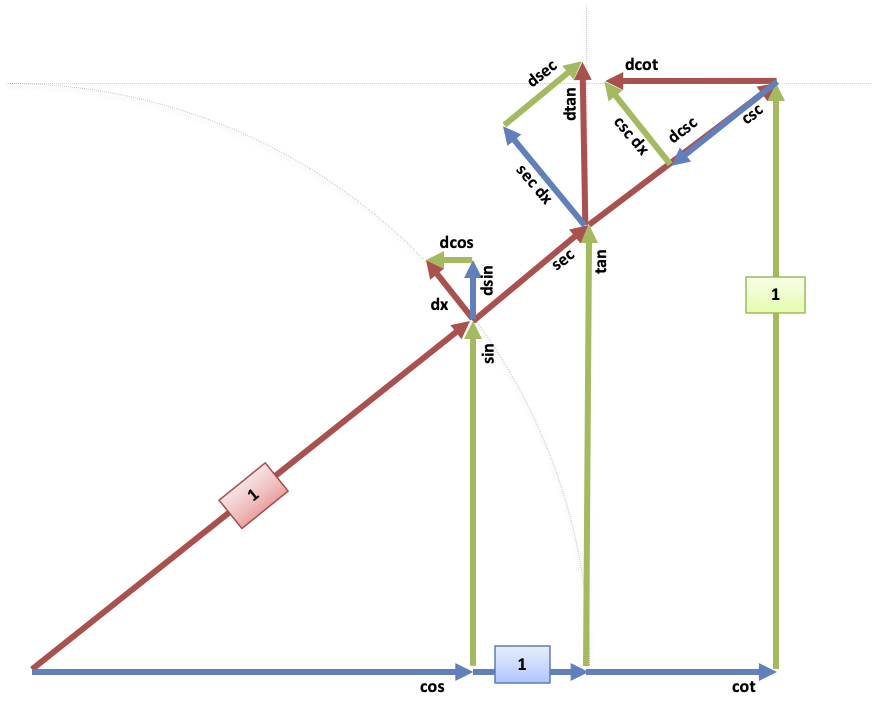
Again, the intuition: these mini red/green/blue triangles (which are all similar!) show the changes.
Appendix: Exponential Behavior
Remember how we didn't think a derivative should be based on the same function? Well,
$\tan' = \sec^2 = 1 + \tan^2$
which means tangent grows faster than exponential: it grows based on its own square (vs. "just" the current value).
We see that $\tan(x)$ beats $e^x$ in a race, and exponentials are no slouch! (I'm looking forward to "this is growing tangentially" to be the new catchphrase.)
Appendix: Other mini-triangle layouts
There's other ways we could arrange the mini-triangle. I think it's easiest when the change along the perimeter is mapped to the side of length 1.
But, when finding $\tan'$, you could use the red/blue/green ratios from the 1/cos/sin triangle and find:
$\tan' = \sec \frac{1}{\cos} = \sec^2$
The scale of $\sec$ is the same, but the unknown side is of length $\frac{1}{\cos} dx$. Different approach, same result.