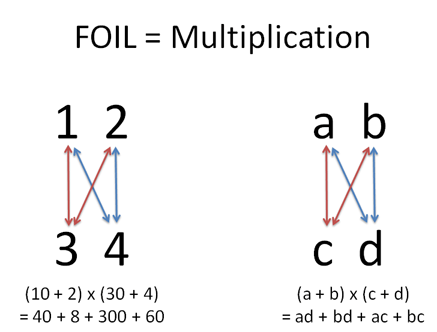
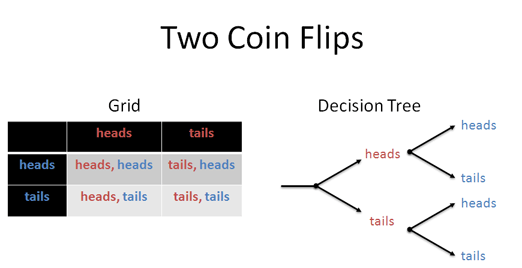
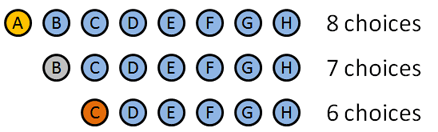Why do we multiply combinations?

When working on a combination problem, we usually multiply. But sometimes addition shows up -- how do we know which is which?

Here's a few mental models I use to keep them straight.

Mental Model: Different Dimensions

Let's take a simple situation: You have 4 shirts and 8 pants, how many outfits can you make?

In essence, you are picking a spot on this grid:

Shirts and Pants exist in separate dimensions, whose area represents distinct solutions. We can pick any spot in the grid and we have 4 x 8 = 32 options.

Now, suppose we had 4 shirts and 8 pants and had to pick a single item to sell. Here, they lie along the same "clothing item" dimension:

We can randomly pick any point along the line and have 4 + 8 = 12 options.

Think "different dimensions vs. same dimesion" or "grid vs. line".

Mental Model: AND vs OR

Another interpretation is AND (multiplication) vs. OR (addition).

Let's say we must pick one of 4 shirts AND one of 8 pants. We need both to stay out of trouble. The scenario is:

pick among 4 shirts AND among 8 pants = 4 * 8 = 32 choices

What if McDonald's softens their regulations and allows a shirt OR pants? (But not both -- yikes.) Then, we have:

pick among 4 shirts OR among 8 pants = 4 + 8 = 12 choices

Writing out the scenario is often easier to think through, especially with numerous dimensions (shirts, pants, hats, shoes).

As you internalize the analogies, you'll quickly recognize whether multiplication or addition is needed.

Example: Combination & Permutation Formula

Let's go meta for a minute. The permutation formula is:

$\displaystyle{ P(n,k) = \frac{n!}{(n-k)!} }$

How can we think about this?

The numerator ($n!$) is the max volume assuming each of the $n$ choices has its own dimension. The number of rearrangements of 8 people is 8 * 7 * 6 * 5 * 4 * 3 * 2 * 1.

But suppose we only care about the first 3 decisions -- picking a Gold, Silver and Bronze among 8 contestants. In this case, we shrink our solution space by dividing out the 5 dimensions we aren't using (which has 5! options on its own). We are left with 8! / 5! = 8 * 7 * 6 = 336 choices, with the general formula $\frac{n!}{(n-k)!}$.

(If multiplication creates dimensions, then division should remove them.)

Now, let's say the medals are identical: we're giving a tin can to 3 out of 8 people. We need to further remove dimensions, because we have 3! = 3 * 2 * 1 = 6 redundancies for each permutation in our solution space. We again shrink our solution space:

$\displaystyle{C(n,k) = \frac{\text{permutation count}}{\text{redundancies}} = \frac{P(n,k)}{k!} }$

(I imagine the solution space volume getting denser.)

Ah! That's what's happening with the combination and permutation formula. We create the max volume and shrink it by the dimensions we are not using. Mentally translate the scenario into a version that makes sense to you.

Example: Flipping Coins

Here's how I think through a few sample problems.

You flip a coin 10 times. How many ways can you get at least 7 heads?

First off, the total number of possibilities is 2^10 = 1024. Intuitively, I see each flip as a decision along a different dimension, not the same number line. This means we have 2 * 2 * 2 *... possibilities, not 2 + 2+ 2 + ... possibilities.

Geometrically, this would be a 10-dimensional "choice space", or, written out:

(Heads OR tails) AND (Heads OR tails) AND (Heads OR tails) AND ...

Ok. Now, how can we get at least 7 heads? That means we had 0 tails [10 heads], 1 tails [9 heads], 2 tails [8 heads], or 3 tails [7 heads].

Switching to the written description, this becomes:

choices we want = (0 tails OR 1 tail OR 2 tails OR 3 tails)

Given our 10 flips, the number of outcomes are:

0 tails = 1 choice (all heads)
1 tail = 10 choices (exactly one flip was tails)
2 tails = C(10,2) = 10*9/(2*1) = 45 choices based on the combination formula
3 tails = C(10,3) = 10 * 9 * 8 / (3 * 2 * 1) = 720 / 6 = 120 choices

So, the total is

choices we want = (1 + 10 + 45 + 120) = 176

And for kicks, the chance of seeing this happen is:

176 / 1024 = 17.2%

Multiplication goes beyond "repeated addition". It's a general notion of combining for which I'm still discovering interpretations. Let's not get tied into a single meaning.

Happy math.

Appendix: Computer Programming

Turning AND/OR statements into arithmetic maps nicely to Boolean logic.

If A and B are variables with the values 1 or 0, we can write:

A AND B = A * B
A OR B = A + B

In most languages, a positive number evaluates to "true", so A + B = 2 is true. Note that this OR is an "inclusive OR" that allows both values to be true. To force an exclusive OR, we could take the remainder after dividing by two:

A XOR B = (A + B) % 2

Most programming languages have separate operators for AND (&&), OR (||) and XOR (^), but it's nice seeing how logic works with regular arithmetic.

Additionally, "if/then/else" statements can be converted to arithmetic.

If y is a variable (1 or 0) that determines a result, instead of:

if (y) {
   result = ResultIfTrue;
}
else {
   result = ResultIfFalse;
}

we can use the single statement:

result = y * ResultIfTrue + (1 - y) * ResultIfFalse

This version avoids the needs for branching, which is expensive for a CPU, and is a formula we can optimize with Calculus (used in machine learning algorithms).

Topic Reference

Combination

Math

Join 450k Monthly Readers

Enjoy the article? There's plenty more to help you build a lasting, intuitive understanding of math. Join the newsletter for bonus content and the latest updates.

Navigate a Grid Using Combinations And Permutations

Puzzles can help develop your intuition -- figuring how to navigate a grid helped me understand combinations and permutations.

Suppose you're on a 4 × 6 grid, and want to go from the bottom left to the top right. How many different paths can you take? Avoid backtracking -- you can only move right or up.

Spend a few seconds thinking about how you'd figure it out.

Insight: Convert Pictures To Text

When considering the possible paths (tracing them out with your finger), you might whisper "Up, right, up, right...".

Why not write those thoughts down? Using "u" and "r" we can write out a path:

r r r r r r r u u u u

That is, go all the way right (6 r's), then all the way up (4 u's). The path in the diagram would be:

r r r r u u u u r r

Using the text interpretation, the question becomes "How many ways can we re-arrange the letters rrrrrruuuu?"

Ah, the ubiquitous combination/permutation problem -- never thought it'd be useful, eh?

Understanding Combinations And Permutations

There's several ways to see combination and permutation problems. Once the first explanation clicks, we can go back and see it a different way. When trying to build math intuition for a problem, I imagine several mental models circling a core idea. Starting with one insight, I work around to the others.

Approach 1: Start The Same

Instead of having 6 rights at 4 ups, imagine we start with 10 rights (r r r r r r r r r r).

Clearly this won't do: we need to change 4 of those rights into ups. How many ways can we pick 4 rights to change?

Well, we have 10 choices for the first 'right' to convert (see the combinations article). And 9 for the second, 8 for the third, and 7 choices for the final right-to-up conversion. There are 10 * 9 * 8 * 7 = 10!/6! = 5040 possibilities.

But, wait! We need to remove the redundancies: after all, converting moves #1 #2 #3 and #4 (in that order) is the same as converting #4 #3 #2 #1. We have 4! (4 * 3 * 2 * 1 = 24) ways to rearrange the ups we picked, so we finally get:

$\displaystyle{\frac{(10!/6!)}{4!} = \frac{5040}{24} = 210 }$

We're just picking the items to convert (10!/6!) and dividing out the redundancies (4!).

Approach 2: Just Use the Combination Formula

Halfway through that explanation, you might have realized we were recreating the combination formula:

$\displaystyle{C(10,4) = 210}$

That's the shortcut when you know order doesn't matter. However, sometimes I'm not sure whether I need a permutation or combination from the outset. While saying "Just use C(10,4)" may be accurate, it's not helpful as a teaching tool. Sometimes it helps to re-create the situation on your own.

Approach 3: Start Different

Here's another approach: instead of letting each r and u be interchangeable, label the 'right' moves r1 to r6, and the 'up' moves u1 to u4. How many ways can we re-arrange these 10 items?

This question is easy: 10! = 3,628,800 (wow, big number). We have 10 choices for the 1st move, 9 for the second, and so on, until we have 2 choices for the 9th and only 1 for the last. Cool.

Of course, we know that "r1 r2 u1 u2" is the same path as "r2 r1 u2 u1". We can shuffle the r's and u's in their own subgroups and the path will stay the same.

How many ways can we shuffle all 10? 10! = 3,628,800
How many ways can we shuffle 6 r's? 6! = 720
How many ways can we shuffle 4 u's? 4! = 24

So, we start with the total number of possibilities (10! = 3,628,800) and divide out the cases where we shuffle the r's (6! = 720) and the u's (4! = 24):

$\displaystyle{10! / 6! / 4! = 10! / (6! \cdot 4!) = 210}$

Neat! It's cool seeing the same set of multiplications and divisions in different ways, just by regrouping them.

Why is this useful?

One goal is to learn how problems can be transformed. Remember that painting of the old lady & young woman?

Do you see both? Can you switch between them? Isn't that cool?

Part of the fun of the grid-path puzzle is seeing how to look at a problem using a visual or text metaphor. The more math you learn, the more models you have available, and you can turn problems into each other.

This doesn't have to be "practical" -- it's fun to see how listing out paths can be be done simply using letters on paper.

In math lingo, problems which can be converted to each other are "isomorphic". Mathematically, they may be the same -- but from a human perspective, one may be easier than the other (like seeing the old woman or young woman first).

For the grid puzzle, we used each perspective where comfortable:

Visualizing the grid to understand the general problem and see a single path.
Write the paths as text to see the general format of all paths & an easy method to enumerate them

And that's the key lesson: It's completely fine to use one model to understand the idea, and another to work out the details. Math becomes difficult when we think there's only one way to approach it.

Variations and Extensions

Now that we've been building our mental models, let's tackle some harder problems.

Imagine your "grid" is actually in 3 dimensions. This is harder to draw, but the text representation keeps on working. Let's say we have a cube (x, y and z dimensions) that is 5 units long on each side. How many paths are there from one corner to its opposite?

Hrm. In this case, I might try the second approach, where we listed out all the possibilities. Assume we label each move differently: we have 5 uniquely-labeled moves of each type (x1-x5, y1-y5, z1-z5). We can arrange these in 15! ways (it's huge: 1.3 trillion). But, we need to remember to divide out the redundancies for each dimension.

There are 5! ways to rearrange the 5 identical motions in each direction, and we divide them out:

$\displaystyle{15! / 5! / 5! / 5! = 15!/(5!\cdot 5!\cdot 5!) = 756,756}$

Wow, that's huge number of paths on a small cube! Earlier today you'd have trouble with the question -- I know I would have. But starting with the grid example and converting it to text, we've beefed up our model to handle 3 dimensions. Paths in four, five or 10-d should be no problem.

Redefining The Problem

Here's the fun part: instead of changing how we see the solution, why not change the problem? What else could "Find paths on a grid" represent?

Trap platform: Let's say you're making a set of trapdoors 4 × 6, with only 1 real path through (the others drop you into a volcano). What are the chances someone randomly walks through? With a 4×6 it's 210, as before. With a 12×12 grid it's 24!/12!12! = 2.7 million paths, with only 1 correct one.
Order of operations: Suppose you have 10 sets of exercises to do: 4 identical leg exercises, and 6 identical arm exercises. How many different routines can you pick? This is the same as navigating the path, except the axis labels are "legs" and "arms" instead of "right" and "up".
Random walk. Suppose we know an object moves randomly up or right. What's the chance it hits our desired endpoint after 10 steps? Well, there are 2^10 = 1024 ways to move up or right (pick "u" or "r" 10 times), and 210 ways to get to our exact destination. Therefore, you can expect to hit our spot 210 / 1024 = 20.5% of the time!

Here's a calculator to play with a few variations:

Onward and Upward

Puzzles are a fun way to learn new mental models, and deepen your understanding for the ones you're familiar with. While I might "know" combinations and permutations, it's not until I recognize them in the wild do I feel really comfortable. Ideas do no good sitting inside your head like artifacts in a museum -- they need to be taken out and played with. Happy math.

Topic Reference

Combination

Permutation

Math

Join 450k Monthly Readers

Enjoy the article? There's plenty more to help you build a lasting, intuitive understanding of math. Join the newsletter for bonus content and the latest updates.

How To Understand Combinations Using Multiplication

Multiplication is a wonderful little operation. Depending on the context, it can

Scale or stretch a number
Rotate a vector, without needing sine or cosine

And today we’ll see yet another use: listing combinations.

Revisiting multiplication has a few uses:

It demystifies other parts of math. The binomial theorem, Boolean algebra (used in computer circuits) and even parts of calculus become easier with a new interpretation of “multiplication”.
It keeps our brain fresh.Math gives us models to work with, and it’s good to see how one model can have many uses. Even a wrench can drive nails, once you understand the true nature of “being a hammer” (very Zen, eh?).

The long multiplication you learned in elementary school is quite useful: we can find the possibilities of several coin flips, for example. Let’s take a look.

You’ve Been Making Combinations All Along

How would you find 12 × 34? It’s ok, you can do it on paper:

“Well, let’s see… 4 times 12 is 48. 3 times 12 is 36… but it’s shifted over one place, so it’s 360. Add 48 and 360 and you get… uh… carry the 1… 408. Phew.”

Not bad. But instead of doing 12 × 34 all at once, break it into steps:

Expanding Multiplication

What’s happening? Well, 4 × 12 is actually “4 x (10 + 2)” or “40 + 8″, right? We can view that first step (blue) as two separate multiplications (4×10 and 4×2).

We’re so used to combining and carrying that we merge the steps, but they’re there. (For example, 4 × 17 = 4 x (10 + 7) = 40 + 28 = 68, but we usually don’t separate it like that.)

Similarly, the red step of “3 × 12″ is really “30 × 12″ — the 3 is in the tens column, after all. We get “30 x (10 + 2)” or “300 + 60″. Again, we can split the number into two parts.

What does this have to do with combinations? Hang in there, you’ll see soon enough.

Curses, Foiled Again

Take a closer look at what happened: 12 × 34 is really (10 + 2) x (30 + 4) = 300 + 40 + 60 + 8. This breakdown looks suspiciously like algebra equation (a + b) * (c + d):

Listing combinations

And yes, that’s what’s happening! In both cases we’re multiplying one “group” by another. We take each item in the red group (10 and 2) and combine it with every element of the blue group (30 and 4). We don’t mix red items with each other, and we don’t mix blue items with each other.

This combination technique is often called FOIL (first-inside-outside-last), and gives headaches to kids. But it’s not a magical operation! It’s just laying things out in a grid. FOIL is already built into the way we multiply!

Foil and multiplication

When doing long multiplication, we “know” we’re not supposed to multiply across: you don’t do 1 × 2, because they’re in the same row. Similarly, you don’t do a x b, because they’re in the same parenthesis. We only multiply “up and down” — that is, we need an item from the top row (1 or 2, a or b) and an item from the bottom row (3 or 4, c or d).

Everyday multiplication (aka FOIL) gives us a way to crank out combinations of two groups: one from group A, another from group B. And sometimes it’s nice having all the possibilities as an equation.

Examples Make It Click

Let’s try an example. Suppose we want to find every combination of flipping a coin twice. There’s a few ways to do it, like using a grid or decision tree:

Decision grid and tree

That’s fine, but let’s be different. We can turn the question into an equation using the following rules:

addition = OR. We can get heads OR tails: (h+t)
multiplication = AND. We have a first toss AND a second toss: (h+t) * (h+t)

Wow! How does this work?

Well, we really just want to crank out combinations, just like doing (a+b) * (c+d) = ac + bc + ad + bd. Looking carefully, this format means we pick a OR b, and combine it with one of c OR d.

When we see an addition (a+b), we know it means we must choose one variable: this OR that. When we see a multiplication (group1 * group2), we know it means we take one item from each: this AND that.

The shortcuts “AND = multiply” & “OR = add” are simply another way to describe the relationship inside the equation. (Be careful; when we say three hundred and four, most people think 304, which is right too. This AND/OR trick works in the context of describing combinations).

So, when all’s said and done, we can turn the sentence “(heads OR tails) AND (heads OR tails)” into:

$\displaystyle{(h + t)\cdot(h + t)}$

And just for kicks, we can multiply it out:

$\displaystyle{(h + t) \cdot (h + t) = h^2 + th + ht + t^2 = h^2 + 2ht + t^2}$

The result “h² + 2ht + t²” shows us every possibility, just like the grids and decision trees. And the size (coefficient) of each combination shows the number of ways it can happen:

h^2: There’s one way to get two heads (h² = hh = heads AND heads)
2ht: There’s two ways to get a head and tails (ht, th)
t^2: There’s one way to get two tails (tt)

Neato. The sum of the coefficients is 1 + 2 + 1 = 4, the total number of possibilities. The chance of getting exactly one heads and one tails is 2/4 = 50%. We figured this out without a tree or grid — regular multiplication does the trick!

Grids? Trees? I Figured That Out In My Head.

Ok, hotshot, let’s expand the scope. How many ways can we get exactly 2 heads and 2 tails with 4 coin flips? What’s the chance of getting 3 or more heads?

Our sentence becomes: “(heads OR tails) AND (h OR t) AND (h OR t) AND (h OR t)”

$\displaystyle{(h+t)^4 = h^4 + 4h^3t + 6h^2t^2 + 4ht^3 + t^4}$

Looking at the result (it looks hard but there are shortcuts), there are 6 ways to get 2 heads and 2 tails. There’s 1 + 4 + 6 + 4 + 1 = 16 possibilities, so there’s only a 6/16 = 37.5% chance of having a “balanced” result after 4 coin flips. (It’s a bit surprising that it’s much more likely to be uneven than even).

And how many ways can we get 3 or more heads? Well, that means any components with h³ or h⁴: 4 + 1 = 5. So we have 5/16 = 31.25% chance of 3 or more heads.

Sometimes equations are better than grids and trees — look at how much info we crammed into a single line! Formulas work great when you have a calculator or computer handy.

But most of all, we have another tool in our box: we can write possibilities as equations, and use multiplication to find combinations.

Where Next?

There’s a few areas of math that benefit from seeing multiplication in this way:

Binomial Theorem. This scary-sounding theorem relates (h+t)^n to the coefficients. If you’re clever, you realize you can use combinations and permutations to figure out the exponents rather than having to multiply out the whole equation. This is what the binomial theorem does. We’ll cover more later — this theorem shows up in a lot of places, including calculus.
Boolean Algebra. Computer geeks love converting conditions like OR and AND into mathematical statements. This type of AND/OR logic is used when designing computer circuits, and expressing possibilities with equations (not diagrams) is very useful. The fancy name of this technique is Boolean Algebra, which we’ll save for a rainy day as well.
Calculus. Calculus gets a double bonus from this interpretation. First, the binomial theorem makes working with equations like x^n much easier. Second, one view of calculus is an “expansion” of multiplication. Today we got practice thinking that multiplication means a lot more than “repeated addition”. (“12 × 34″ means 12 groups of 34, right?)
More advanced combinations. Let’s say you have 3 guests (Alice, Bob, and Charlie) and they are bringing soda, ice cream, or yogurt. Someone knocks at the door — what are the possibilities? (a + b + c) * (s + i + y). The equation has it all there.

So you can teach an old dog like multiplication new tricks after all. Well, the tricks have always been there — it’s like discovering Fido has been barking poetry in morse code all this time.

And come to think of it, maybe we’re the animal that learned a new trick. The poetry was there, staring us in the face and we just didn’t recognize it (12 × 34 is based on combinations!). I know I had some forehead-slapping moments after seeing how similar combinations and regular multiplication really were.

Happy math.

Topic Reference

Combination

Math

Join 450k Monthly Readers

Enjoy the article? There's plenty more to help you build a lasting, intuitive understanding of math. Join the newsletter for bonus content and the latest updates.

Easy Permutations and Combinations

I’ve always confused “permutation” and “combination” — which one’s which?

Here’s an easy way to remember: permutation sounds complicated, doesn’t it? And it is. With permutations, every little detail matters. Alice, Bob and Charlie is different from Charlie, Bob and Alice (insert your friends’ names here).

Combinations, on the other hand, are pretty easy going. The details don’t matter. Alice, Bob and Charlie is the same as Charlie, Bob and Alice.

Permutations are for lists (order matters) and combinations are for groups (order doesn’t matter).

You know, a "combination lock" should really be called a "permutation lock". The order you put the numbers in matters.

A true "combination lock" would accept both 10-17-23 and 23-17-10 as correct.

Permutations: The hairy details

Let’s start with permutations, or all possible ways of doing something. We’re using the fancy-pants term “permutation”, so we’re going to care about every last detail, including the order of each item. Let’s say we have 8 people:

1: Alice
2: Bob
3: Charlie
4: David
5: Eve
6: Frank
7: George
8: Horatio

How many ways can we award a 1st, 2nd and 3rd place prize among eight contestants? (Gold / Silver / Bronze)

$permuation example medals$

We’re going to use permutations since the order we hand out these medals matters. Here’s how it breaks down:

Gold medal: 8 choices: A B C D E F G H (Clever how I made the names match up with letters, eh?). Let’s say A wins the Gold.
Silver medal: 7 choices: B C D E F G H. Let’s say B wins the silver.
Bronze medal: 6 choices: C D E F G H. Let’s say… C wins the bronze.

We picked certain people to win, but the details don’t matter: we had 8 choices at first, then 7, then 6. The total number of options was $8 * 7 * 6 = 336$.

Let’s look at the details. We had to order 3 people out of 8. To do this, we started with all options (8) then took them away one at a time (7, then 6) until we ran out of medals.

We know the factorial is:

$\displaystyle{ 8! = 8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1 }$

Unfortunately, that does too much! We only want $8 * 7 * 6$. How can we “stop” the factorial at 5?

This is where permutations get cool: notice how we want to get rid of $5 * 4 * 3 * 2 * 1$. What’s another name for this? 5 factorial!

So, if we do 8!/5! we get:

$\displaystyle{\frac{8!}{5!} = \frac{8 \cdot 7 \cdot 6 \cdot 5 \cdot 4 \cdot 3 \cdot 2 \cdot 1}{5 \cdot 4 \cdot 3 \cdot 2 \cdot 1} = 8 \cdot 7 \cdot 6}$

And why did we use the number 5? Because it was left over after we picked 3 medals from 8. So, a better way to write this would be:

$\displaystyle{\frac{8!}{(8-3)!}}$

where 8!/(8-3)! is just a fancy way of saying “Use the first 3 numbers of 8!”. If we have n items total and want to pick k in a certain order, we get:

$\displaystyle{\frac{n!}{(n-k)!}}$

And this is the fancy permutation formula: You have n items and want to find the number of ways k items can be ordered:

$\displaystyle{P(n,k) = \frac{n!}{(n-k)!}}$

Combinations, Ho!

Combinations are easy going. Order doesn’t matter. You can mix it up and it looks the same. Let’s say I’m a cheapskate and can’t afford separate Gold, Silver and Bronze medals. In fact, I can only afford empty tin cans.

How many ways can I give 3 tin cans to 8 people?

Well, in this case, the order we pick people doesn’t matter. If I give a can to Alice, Bob and then Charlie, it’s the same as giving to Charlie, Alice and then Bob. Either way, they’re equally disappointed.

This raises an interesting point — we’ve got some redundancies here. Alice Bob Charlie = Charlie Bob Alice. For a moment, let’s just figure out how many ways we can rearrange 3 people.

Well, we have 3 choices for the first person, 2 for the second, and only 1 for the last. So we have $3 * 2 * 1$ ways to re-arrange 3 people.

Wait a minute… this is looking a bit like a permutation! You tricked me!

Indeed I did. If you have N people and you want to know how many arrangements there are for all of them, it’s just N factorial or N!

So, if we have 3 tin cans to give away, there are 3! or 6 variations for every choice we pick. If we want to figure out how many combinations we have, we just create all the permutations and divide by all the redundancies. In our case, we get 336 permutations (from above), and we divide by the 6 redundancies for each permutation and get 336/6 = 56.

The general formula is

$\displaystyle{C(n,k) = \frac{P(n,k)}{k!}}$

which means “Find all the ways to pick k people from n, and divide by the k! variants”. Writing this out, we get our combination formula, or the number of ways to combine k items from a set of n:

$\displaystyle{C(n,k) = \frac{n!}{(n-k)!k!}}$

Sometimes C(n,k) is written as:

$\displaystyle{\binom {n}{k}}$

which is the the binomial coefficient.

A few examples

Here’s a few examples of combinations (order doesn’t matter) from permutations (order matters).

Combination: Picking a team of 3 people from a group of 10. $C(10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.

Permutation: Picking a President, VP and Waterboy from a group of 10. $P(10,3) = 10!/7! = 10 * 9 * 8 = 720$.
Combination: Choosing 3 desserts from a menu of 10. C(10,3) = 120.

Permutation: Listing your 3 favorite desserts, in order, from a menu of 10. P(10,3) = 720.

Don’t memorize the formulas, understand why they work. Combinations sound simpler than permutations, and they are. You have fewer combinations than permutations.

Topic Reference

Combination

Permutation

Math

Join 450k Monthly Readers

Enjoy the article? There's plenty more to help you build a lasting, intuitive understanding of math. Join the newsletter for bonus content and the latest updates.