It's easy to take math too literally. When we read The Tortoise and the Hare, we know it's not about zoology -- there's a deeper wisdom.
Why can't we treat equations like one of Aesop's fables, with a lesson buried inside?
Take a look at the Pythagorean Theorem. It seems to be about triangles, right?
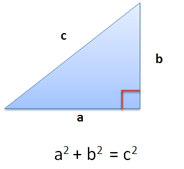
Well, sure. But is it only that? Seeing the equation:
![]()
has a literal interpretation "The sides of a triangle have a specific mathematical relationship."
Ok, fine. That's some nice zoology. Stepping back, what's really happening?
The sides of a triangle, which point in different directions, have a mathematical relationship.
Or better yet:
Two objects, which exist in different dimensions, can still be compared.
Here's an analogy: Who's the better athlete, Michael Jordan or Muhammad Ali?
We shouldn't ask who has a better jump shot or uppercut -- that comparison stays within a single dimension, clearly favoring one or the other. A better comparison would encompass all dimensions: Who was more dominant compared to the competition? Who held more championships? Who advanced the sport more?
Ah. We need a different type of "expansive" comparison to help each component see the other side.
In the triangle case, we have an "A direction" (East/West) and a "B direction" (North/South). Instead of comparing them directly, we square them to make area. Why?
Here's an intuition. Individual directions point in a single direction within our 2d universe. But area spans every direction available in our universe. By converting a single direction to its square (which points in all directions), we have a common "all directions" format that can be compared. It becomes "universal area vs. universal area" and not "pointing North vs. pointing East" (aka jump shots vs. uppercuts).
Will any type of universal self-comparison work? (Squaring, cubing, etc.)
No, unfortunately. The Pythagorean Theorem is special because it shows the specific comparison of squaring ($a^2 + b^2 = c^2$) keeps a simple relationship between the whole and its parts. There's probably a relationship for cubing, but it's not as clear cut.
Pythagorean Theorem Fact: The sides of a right triangle follow $a^2 + b^2 = c^2$
Pythagorean Theorem Wisdom: To compare different things, find a universal way to compare them. (Specifically, square yourself to create area.)
Equations aren't so boring when you look for the moral of the story, right?
Appendix: Visually Creating Area
In the Pythagorean Theorem, we can imagine spinning our 1d lines into area and comparing that. Here, we can spin each side into a circle:
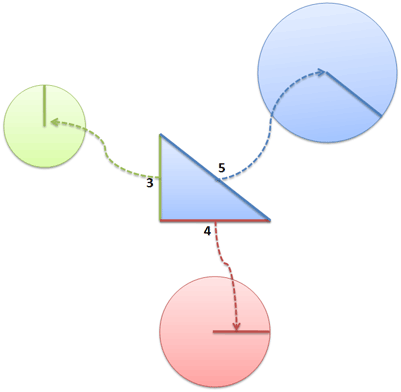
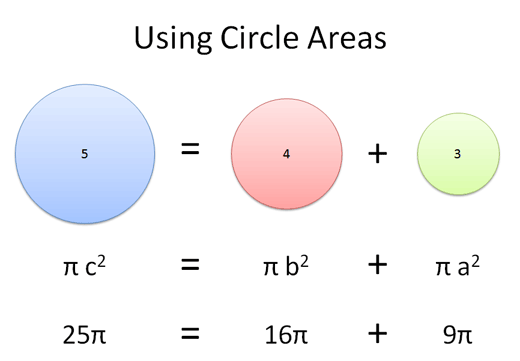
And yowza, the area matches up!
This is a demonstration of the theorem; the proof shows that area will always combine neatly like this. (Read more.)
Appendix: Vector Pythagorean Theorem
We can make our "self comparison" analogy more technical with vectors.
- $\vec a$ is the vector $(a, 0)$
- $\vec b$ is a vector in a different dimension, $(0, b)$
- $\vec c$ is a vector made from both: $\vec c = \vec a + \vec b = (a, 0) + (0, b) = (a,b)$
The Pythagorean Theorem says "If we compare each item to itself, the combined self-comparisons of $\vec a$ and $\vec b$ equal the self-comparison of $\vec c$".
(c compared to itself) = (a compared to itself) + (b compared to itself)
In the vector world, what's a self-comparison? A dot product with yourself.
The Pythagorean Theorem is stating:
![]()
which works because:
![]()
(Since $\vec a$ and $\vec b$ are perpendicular, their dot product is zero.)
And for the parts:
![]()
This specific self-comparison maintains a simple relationship between the whole and its parts (addition).
A simple glance at two vectors doesn't offer a built-in way to compare them; instead, use a derived scalar (single number) that allows a comparison to be made.