Here's the typical presentation for slope-intercept form for a line:
![]()
What goes through our head the first time we see this?
Ok, y is usually the final value in an equation. It's based on two parts... mx and b. If x goes up by 1 let's say, we only change y by... m.
Hrm, let's try an example. If m=.3, and x goes from 0 to 10, we go up by 10 * .3 = 3. Ok. Got that part.
Now what does b do? It adds something on top of whatever we just figured out. If x = 0, I guess we just have y = b.
There's a lot of Math <> English translation. In math jargon, we say the slope (m) determines the direct rate of change between x and y, and the y-intercept (b) adds a starting value.
Ugh. It's abstract and doesn't resonate. Here's a more natural wording:
![]()
Makes sense, right? Start somewhere, make a change, get to the new location.
Zooming in, we realize a change has two parts: how fast are we changing, and for how long?
![]()
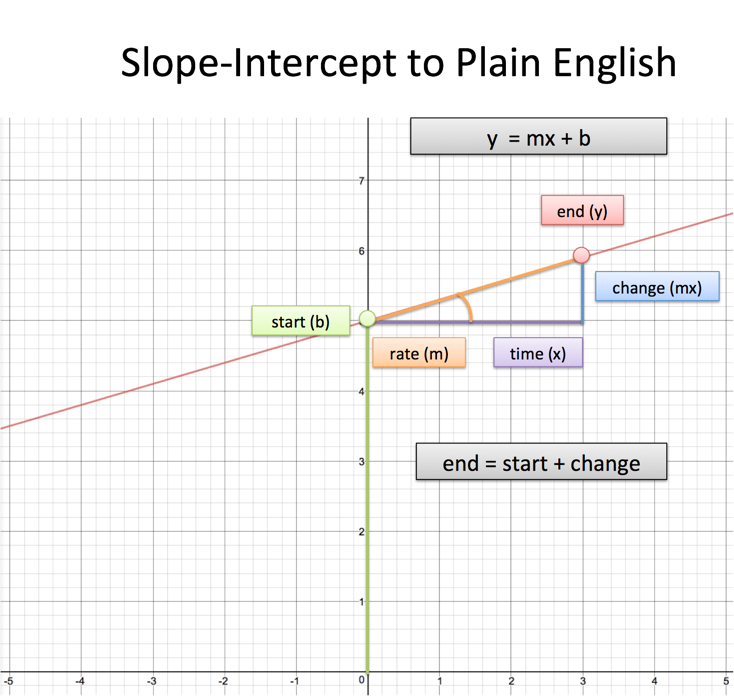
Ah. I can see the role of each of the pieces. Turning this into succint math notation:
![]()
"Start at b, add the rate of change (m) times the duration (x), and you end up at y."
We aren't forced to graph the equation and describe b as the "y intercept". Who thinks (or talks) like that?
In plain English:
- b is our starting point
- x is the change we intend to make
- m is the percentage (rate) of the change we actually see
Boom. Later, if we decide to graph our line (fun fun), then b is the height on the y-axis when x=0. But thinking in terms of our starting value (the bias) just clicks better.
The graphed line is a list of all possible outcomes under some set of circumstances. We might not wait at all (x =0), or wait for a bit (x=1), wait for a long time (x = 100), or look back in time (x = -3). The line shows what would have happened in each of those scenarios.
People claim they don't think in terms of math. Sure, you might not describe things as slope/intercept form, but I'd guess "original + change = new" is pretty familiar to you. Even the simplest equations can use an intuitive wording.
Example: Find the slope-intercept form between two points
Q: Find the equation for a line between (3, 4) and (7, 12)
Let's think about this intuitively. We know ultimately we want an equation of the form:
position = start + change
For the two points we have, let's look at the change:
- Change in x: 7 - 3 = 4
- Change in y: 12 - 4 = 8
Between those points, x changed by 4 and y changed by 8. The rate was 8/4 = 2, so the equation should look like:
position = start + x * 2
We don't know where we started, but whenever x changes, y changes by 2 times that amount.
Ok. Now what was the starting position, when x = 0? Let's see the change between our default value of (0, ?) to (3, 4).
- Change in x: 3 - 0 = 3
- Change in y: 4 - ? [unknown]
Well, if x changed by 3, and the rate of change is 2, then y changed by 3*2 = 6. The original value was therefore 4 - 6 = -2.
- Original point is (0, -2)
The final equation is then:
position = start + change
position = start + x * 2
position = -2 + x * 2
and written in more standard y = mx + b notation,
y = 2x - 2
Let's double check. We start at (0, -2) and go 3 units on the x coordinate. Our final position is 2*3 - 2 = 6 -2 = 4, which matches up with (3, 4).
This approach is slower than a plug-and-chug shortcut, but the idea is to figure out exactly what you're doing:
- Figure out the rate of change between two points (m)
- Using that rate of change, work backwards to find our starting point (b)
Happy math.