Understanding the Birthday Paradox

23 people. In a room of just 23 people there’s a 50-50 chance of at least two people having the same birthday. In a room of 75 there’s a 99.9% chance of at least two people matching.

Put down the calculator and pitchfork, I don’t speak heresy. The birthday paradox is strange, counter-intuitive, and completely true. It’s only a “paradox” because our brains can’t handle the compounding power of exponents. We expect probabilities to be linear and only consider the scenarios we’re involved in (both faulty assumptions, by the way).

Let’s see why the paradox happens and how it works.

Problem 1: Exponents aren’t intuitive

We’ve taught ourselves mathematics and statistics, but let’s not kid ourselves: it’s not natural.

Here’s an example: What’s the chance of getting 10 heads in a row when flipping coins? The untrained brain might think like this:

“Well, getting one head is a 50% chance. Getting two heads is twice as hard, so a 25% chance. Getting ten heads is probably 10 times harder… so about 50%/10 or a 5% chance.”

And there we sit, smug as a bug on a rug. No dice bub.

After pounding your head with statistics, you know not to divide, but use exponents. The chance of 10 heads is not .5/10 but $.5^10$, or about .001.

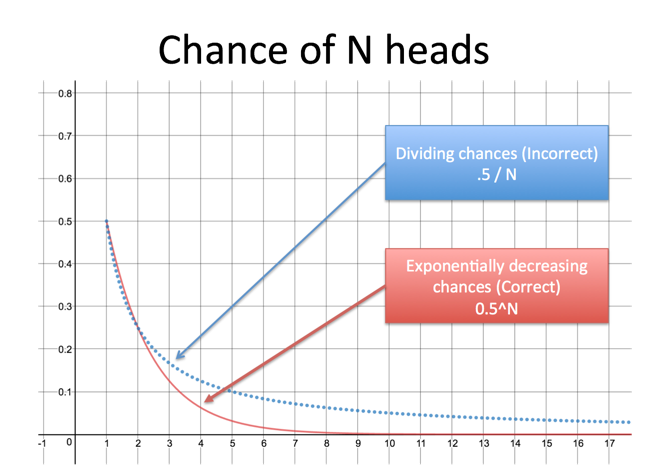
But even after training, we get caught again. At 5% interest we’ll double our money in 14 years, rather than the “expected” 20. Did you naturally infer the Rule of 72 when learning about interest rates? Probably not. Understanding compound exponential growth with our linear brains is hard.

Problem 2: Humans are a tad bit selfish

Take a look at the news. Notice how much of the negative news is the result of acting without considering others. I’m an optimist and do have hope for mankind, but that’s a separate discussion :).

In a room of 23, do you think of the 22 comparisons where your birthday is being compared against someone else’s? Probably.

Do you think of the 231 comparisons where someone who is not you is being checked against someone else who is not you? Do you realize there are so many? Probably not.

The fact that we neglect the 10 times as many comparisons that don’t include us helps us see why the “paradox” can happen.

Ok, fine, humans are awful: Show me the math!

The question: What are the chances that two people share a birthday in a group of 23?

Sure, we could list the pairs and count all the ways they could match. But that’s hard: there could be 1, 2, 3 or even 23 matches!

It’s like asking “What’s the chance of getting one or more heads in 23 coin flips?” There are so many possibilities: heads on the first throw, or the 3rd, or the last, or the 1st and 3rd, the 2nd and 21st, and so on.

How do we solve the coin problem? Flip it around (Get it? Get it?). Rather than counting every way to get heads, find the chance of getting all tails, our “problem scenario”.

If there’s a 1% chance of getting all tails (more like .5^23 but work with me here), there’s a 99% chance of having at least one head. I don’t know if it’s 1 head, or 2, or 15 or 23: we got heads, and that’s what matters. If we subtract the chance of a problem scenario from 1 we are left with the probability of a good scenario.

The same principle applies for birthdays. Instead of finding all the ways we match, find the chance that everyone is different, the “problem scenario”. We then take the opposite probability and get the chance of a match. It may be 1 match, or 2, or 20, but somebody matched, which is what we need to find.

Explanation: Counting Pairs (Approximate Formula)

With 23 people we have 253 pairs:

$\displaystyle{\frac{23 \cdot 22}{2} = 253}$

(Brush up on combinations and permutations if you like).

The chance of 2 people having different birthdays is:

$\displaystyle{1 - \frac{1}{365} = \frac{364}{365} = .997260}$

Makes sense, right? When comparing one person's birthday to another, in 364 out of 365 scenarios they won't match. Fine.

But making 253 comparisons and having them all be different is like getting heads 253 times in a row -- you had to dodge "tails" each time. Let's get an approximate solution by pretending birthday comparisons are like coin flips. (See Appendix A for the exact calculation.)

We use exponents to find the probability:

$\displaystyle{\left(\frac{364}{365}\right)^{253} = .4995}$

Our chance of getting a single miss is pretty high (99.7260%), but when you take that chance hundreds of times, the odds of keeping up that streak drop. Fast.

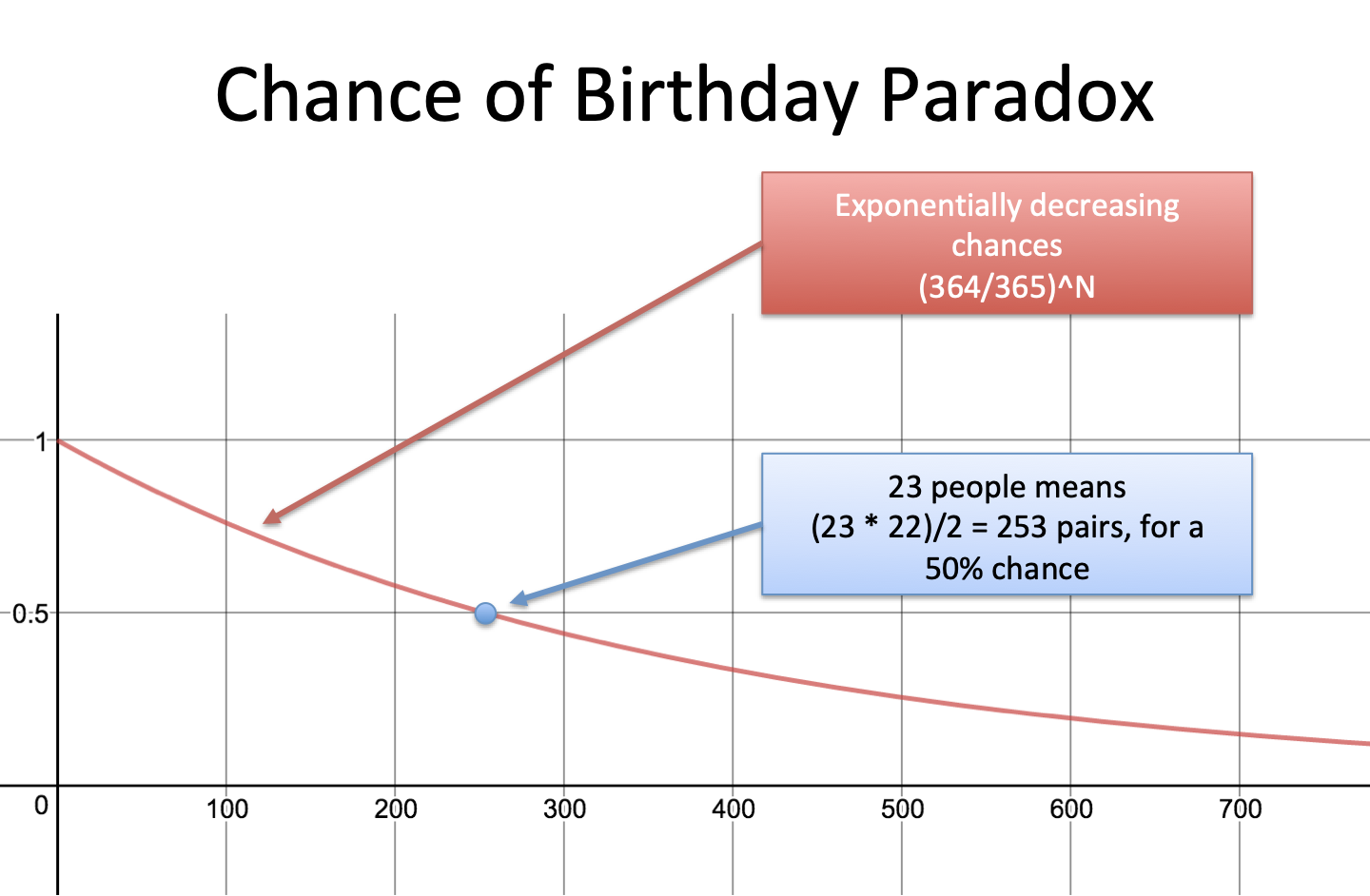
The chance we find a match is: 1 – 49.95% = 50.05%, or just over half! If you want to find the probability of a match for any number of people n the formula is:

$\displaystyle{p(n) = 1 - \left(\frac{364}{365}\right)^{C(n,2)} = 1 - \left(\frac{364}{365}\right)^{n(n-1)/2} }$

Interactive Example

I didn’t believe we needed only 23 people. The math works out, but is it real?

You bet. Try the example below: Pick a number of items (365), a number of people (23) and run a few trials. You’ll see the theoretical match and your actual match as you run your trials. Go ahead, click the button (or see the full page).

As you run more and more trials (keep clicking!) the actual probability should approach the theoretical one.

Examples and Takeaways

Here are a few lessons from the birthday paradox:

$\sqrt{n}$ is roughly the number you need to have a 50% chance of a match with n items. $\sqrt{365}$ is about 20. This comes into play in cryptography for the birthday attack.
Even though there are 2¹²⁸ (1e38) GUIDs, we only have 2⁶⁴ (1e19) to use up before a 50% chance of collision. And 50% is really, really high.
You only need 13 people picking letters of the alphabet to have 95% chance of a match. Try it above (people = 13, items = 26).
Exponential growth rapidly decreases the chance of picking unique items (aka it increases the chances of a match). Remember: exponents are non-intuitive and humans are selfish!

After thinking about it a lot, the birthday paradox finally clicks with me. But I still check out the interactive example just to make sure.

Appendix A: Repeated Multiplication Explanation (Exact Formula)

Remember how we assumed birthdays are independent? Well, they aren’t.

If Person A and Person B match, and Person B and C match, we know that A and C must match also. The outcome of matching A and C depends on their results with B, so the probabilities aren’t independent. (If truly independent, A and C would have a 1/365 chance of matching, but we know it's a 100% guaranteed match.)

When counting pairs, we treated birthday matches like coin flips, multiplying the same probability over and over. This assumption isn’t strictly true but it’s good enough for a small number of people (23) compared to the sample size (365). It’s unlikely to have multiple people match and screw up the independence, so it’s a good approximation.

It’s unlikely, but it can happen. Let’s figure out the real chances of each person picking a different number:

The first person has a 100% chance of a unique number (of course)
The second has a (1 – 1/365) chance (all but 1 number from the 365)
The third has a (1 – 2/365) chance (all but 2 numbers)
The 23rd has a (1 – 22/365) (all but 22 numbers)

The multiplication looks pretty ugly:

$\displaystyle{p(\text{different}) = 1 \cdot \left(1-\frac{1}{365}\right) \cdot \left(1-\frac{2}{365}\right) \cdots \left(1-\frac{22}{365}\right)}$

But there’s a shortcut we can take. When x is close to 0, a coarse first-order Taylor approximation for $e^x$ is:

$\displaystyle{e^x \approx 1 + x}$

$\displaystyle{ 1 - \frac{1}{365} \approx e^{-1/365}}$

Using our handy shortcut we can rewrite the big equation to:

$\displaystyle{p(\text{different}) \approx 1 \cdot e^{-1/365} \cdot e^{-2/365} \cdots e^{-22/365}}$

$\displaystyle{p(\text{different}) \approx e^{(-1 -2 -3 ... -22)/365}}$

$\displaystyle{p(\text{different}) \approx e^{-(1 + 2 + ... 22)/365}}$

But we remember that adding the numbers 1 to n = n(n + 1)/2. Don’t confuse this with n(n-1)/2, which is C(n,2) or the number of pairs of n items. They look almost the same!

Adding 1 to 22 is (22 * 23)/2 so we get:

$\displaystyle{p(\text{different}) \approx e^{-((23 \cdot 22) /(2 \cdot 365))} = .499998}$

Phew. This approximation is very close, plug in your own numbers below:

Good enough for government work, as they say. If you simplify the formula a bit and swap in n for 23 you get:

$\displaystyle{p(\text{different}) \approx e^{-(n^2 / (2 \cdot 365))}}$

and

$\displaystyle{p(\text{match}) = 1 - p(\text{different}) \approx 1 - e^{-(n^2 / (2 \cdot 365))}}$

With the exact formula, 366 people has a guaranteed collision: we multiply by $1 - 365/365 = 0$, which eliminates $p(\text{different})$ and makes $p(\text{match}) = 1$. With the approximation formula, 366 has a near-guarantee, but is not exactly 1: $1 - e^{-365^2 / (2 \cdot 365)} \approx 1$ .

Appendix B: The General Birthday Formula

Let’s generalize the formula to picking n people from T total items (instead of 365):

$\displaystyle{p(\text{different}) \approx e^{-(n^2 / 2 \cdot T)}}$

If we choose a probability (like 50% chance of a match) and solve for n:

$\displaystyle{p(\text{different}) \approx e^{-(n^2 / 2 \cdot T)}}$

$\displaystyle{1 - p(\text{match}) \approx e^{-(n^2 / 2 \cdot T)}}$

$\displaystyle{1 - .5 \approx e^{-(n^2 / 2 \cdot T)}}$

$\displaystyle{-2\ln(.5)\cdot T \approx n^2}$

$\displaystyle{n \approx 1.177 \sqrt{T}}$

Voila! If you take $\sqrt{T}$ items (17% more if you want to be picky) then you have about a 50-50 chance of getting a match. If you plug in other numbers you can solve for other probabilities:

$\displaystyle{n \approx \sqrt{-2\ln(1-m)} \cdot \sqrt{T}}$

Remember that m is the desired chance of a match (it’s easy to get confused, I did it myself). If you want a 90% chance of matching birthdays, plug m=90% and T=365 into the equation and see that you need 41 people.

Wikipedia has even more details to satisfy your inner nerd. Go forth and enjoy.