I’ve always confused “permutation” and “combination” — which one’s which?
Here’s an easy way to remember: permutation sounds complicated, doesn’t it? And it is. With permutations, every little detail matters. Alice, Bob and Charlie is different from Charlie, Bob and Alice (insert your friends’ names here).
Combinations, on the other hand, are pretty easy going. The details don’t matter. Alice, Bob and Charlie is the same as Charlie, Bob and Alice.
Permutations are for lists (order matters) and combinations are for groups (order doesn’t matter).
You know, a "combination lock" should really be called a "permutation lock". The order you put the numbers in matters.

A true "combination lock" would accept both 10-17-23 and 23-17-10 as correct.
Permutations: The hairy details
Let’s start with permutations, or all possible ways of doing something. We’re using the fancy-pants term “permutation”, so we’re going to care about every last detail, including the order of each item. Let’s say we have 8 people:
1: Alice
2: Bob
3: Charlie
4: David
5: Eve
6: Frank
7: George
8: Horatio
How many ways can we award a 1st, 2nd and 3rd place prize among eight contestants? (Gold / Silver / Bronze)
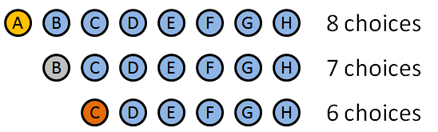
We’re going to use permutations since the order we hand out these medals matters. Here’s how it breaks down:
- Gold medal: 8 choices: A B C D E F G H (Clever how I made the names match up with letters, eh?). Let’s say A wins the Gold.
- Silver medal: 7 choices: B C D E F G H. Let’s say B wins the silver.
- Bronze medal: 6 choices: C D E F G H. Let’s say… C wins the bronze.
We picked certain people to win, but the details don’t matter: we had 8 choices at first, then 7, then 6. The total number of options was $8 * 7 * 6 = 336$.
Let’s look at the details. We had to order 3 people out of 8. To do this, we started with all options (8) then took them away one at a time (7, then 6) until we ran out of medals.
We know the factorial is:
![]()
Unfortunately, that does too much! We only want $8 * 7 * 6$. How can we “stop” the factorial at 5?
This is where permutations get cool: notice how we want to get rid of $5 * 4 * 3 * 2 * 1$. What’s another name for this? 5 factorial!
So, if we do 8!/5! we get:
![]()
And why did we use the number 5? Because it was left over after we picked 3 medals from 8. So, a better way to write this would be:
![]()
where 8!/(8-3)! is just a fancy way of saying “Use the first 3 numbers of 8!”. If we have n items total and want to pick k in a certain order, we get:
![]()
And this is the fancy permutation formula: You have n items and want to find the number of ways k items can be ordered:
![]()
Combinations, Ho!
Combinations are easy going. Order doesn’t matter. You can mix it up and it looks the same. Let’s say I’m a cheapskate and can’t afford separate Gold, Silver and Bronze medals. In fact, I can only afford empty tin cans.
How many ways can I give 3 tin cans to 8 people?
Well, in this case, the order we pick people doesn’t matter. If I give a can to Alice, Bob and then Charlie, it’s the same as giving to Charlie, Alice and then Bob. Either way, they’re equally disappointed.
This raises an interesting point — we’ve got some redundancies here. Alice Bob Charlie = Charlie Bob Alice. For a moment, let’s just figure out how many ways we can rearrange 3 people.
Well, we have 3 choices for the first person, 2 for the second, and only 1 for the last. So we have $3 * 2 * 1$ ways to re-arrange 3 people.
Wait a minute… this is looking a bit like a permutation! You tricked me!
Indeed I did. If you have N people and you want to know how many arrangements there are for all of them, it’s just N factorial or N!
So, if we have 3 tin cans to give away, there are 3! or 6 variations for every choice we pick. If we want to figure out how many combinations we have, we just create all the permutations and divide by all the redundancies. In our case, we get 336 permutations (from above), and we divide by the 6 redundancies for each permutation and get 336/6 = 56.
The general formula is
![]()
which means “Find all the ways to pick k people from n, and divide by the k! variants”. Writing this out, we get our combination formula, or the number of ways to combine k items from a set of n:
![]()
Sometimes C(n,k) is written as:
![]()
which is the the binomial coefficient.
A few examples
Here’s a few examples of combinations (order doesn’t matter) from permutations (order matters).
Combination: Picking a team of 3 people from a group of 10. $C(10,3) = 10!/(7! * 3!) = 10 * 9 * 8 / (3 * 2 * 1) = 120$.
Permutation: Picking a President, VP and Waterboy from a group of 10. $P(10,3) = 10!/7! = 10 * 9 * 8 = 720$.
Combination: Choosing 3 desserts from a menu of 10. C(10,3) = 120.
Permutation: Listing your 3 favorite desserts, in order, from a menu of 10. P(10,3) = 720.
Don’t memorize the formulas, understand why they work. Combinations sound simpler than permutations, and they are. You have fewer combinations than permutations.

