What's algebra about? When learning about variables ($x, y, z$), they seem to "hide" a number:
![]()
What number could be hiding inside of $x$? 2, in this case.
It seems that arithmetic still works, even when we don't have the exact numbers up front. Later on, we might arrange these "hidden numbers" in complex ways:
![]()
Whoa -- a bit harder to solve, but it's possible. Today let's figure out how factoring works and why it's useful.
Polynomials
When we write a polynomial like $x^2 + x = 6$, we can think at a higher level.
We have an unknown number, $x$, which interacts with itself ($x * x = x^2$). We add in the original number ($+ x$) and the result is 6.
$x^2$, $x$ and 6 are all "numbers", but now we're keeping track of how they're made:
- $x^2$ is a component interacting with itself
- $x$ is a component on its own
- 6 is the desired state we want the entire system to become
After the interactions are finished, we should get 6. What number could be hiding inside of $x$ to make this true?
Hrm -- this is tricky. So let's fight with a trick of our own: we can make a different system to track the error in our original one (this is mind-bending, so hang on).
Our original system is $x^2 + x$. The desired state is 6. A new system:
![]()
will track the difference between the original system and the desired state. When are we happiest? When there's no difference:
![]()
Ah! that's why we're so interested in setting polynomials to zero! If we have a system and the desired state, we can make a new equation to track the difference -- and try make it zero. (This is deeper than just "subtract 6 from both sides" -- we're trying to describe the error!)
But... how do we actually get the error to zero? It's still a jumble of components: $x^2$, $x$ and 6 are flying everywhere.
Factor That Mamma Jamma
Factoring the rescue. My intuition: factoring lets us re-arrange a complex system ($x^2 + x - 6$) as a bunch of linked, smaller systems.
Imagine taking a pile of sticks (our messy, disorganized system) and standing them up so they support each other, like a teepee:
/\
(That's a 2-d example, with two sticks).
Remove any stick and the entire structure collapses. If we can rewrite our system:
![]()
as a series of multiplications:
![]()
we've put the sticks in a "teepee". If Component A or Component B becomes 0, the structure collapses, and we get 0 as a result.
Neat! That is why factoring rocks: we re-arrange our error-system into a fragile teepee, so we can break it. We'll find what obliterates our errors and puts our system in the ideal state.
Remember: We're breaking the error in the system, not the system itself.
Onto The Factoring
Learning to "factor an equation" is the process of arranging your teepee. In this case:
![]()
If $x = -3$ then Component A falls down. If $x = 2$, Component B falls down. Either value causes the error to collapse, which means our original system ($x^2 + x$, the one we almost forgot about!) meets our requirements:
- When $x = -3$, the error collapses, and we get $(-3)^2 + -3 = 6$
- When $x = 2$, the error collapses, and we get $2^2 + 2 = 6$
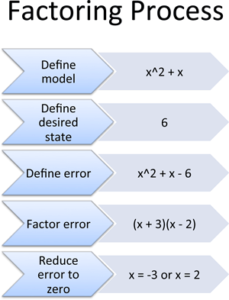
Putting It All Together
I've wondered about the real purpose of factoring for a long, long time. In algebra class, equations are conveniently set to zero, and we're not sure why. Here's what happens in the real world:
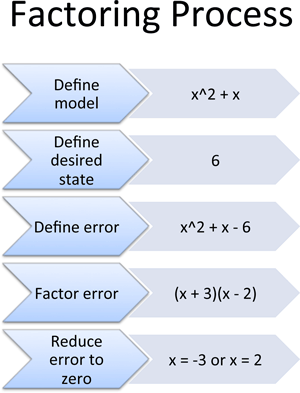
- Define the model: Write how your system behaves ($x^2 + x$)
- Define the desired state: What should it equal? (6)
- Define the error: The error is its own system: Error = actual - desired (i.e., $x^2 + x - 6$)
- Factor the error: Rewrite the error as interlocking components: $(x + 3)(x - 2)$
- Reduce the error to zero: Zero out one component or the other ($x = -3$, or $x = 2$).
When error = 0, our system must be in the desired state. We're done!
Algebra is pretty darn useful:
- Our system is a trajectory, the "desired state" is the target. What trajectory hits the target?
- Our system is our widget sales, the "desired state" is our revenue target. What amount of earnings hits the goal?
- Our system is the probability of our game winning, the "desired state" is a 50-50 (fair) outcome. What settings make it a fair game?
The idea of "matching a system to its desired state" is just one interpretation of why factoring is useful. If you have more, I'd like to hear them!
Appendix
A cheatsheet for the process:
Some more food for thought:
Multiplication is often seen as AND. Component A must be there AND Component B must be there. If either condition is false, the system breaks.
The Fundamental Theorem of Algebra proves you have as many "components" as the highest polynomial. If your highest term is $x^4$, then you can factor into 4 interlocked components (discussion for another day). But this should make sense: if you rewrite an "$x^4$ system" into multiplications, shouldn't there be 4 individual "$x$ components" being multiplied? If there were 3, you could never get to $x^4$, and if there were 5, you'd overshoot and get an $x^5$ term.
Do you have a real-world system in a "teepee" arrangement, where a single failing component collapses the entire structure?
The quadratic formula can "autobreak" any system with $x^2$, $x$ and constant components. There's formulas for complex systems (with $x^3$, $x^4$, or even some $x^5$ components) but they start to get a bit crazy.
Is there any way to prevent a system from having these weak points? (Unfactorable? Non-zeroable?). Don't forget, we thought systems like $x^2 + 1$ were "non-zeroable" until imaginary numbers came along.
Happy math.