The Rule of 72 is a great mental math shortcut to estimate the effect of any growth rate, from quick financial calculations to population estimates. Here’s the formula:
Years to double = 72 / Interest Rate
This formula is useful for financial estimates and understanding the nature of compound interest. Examples:
- At 6% interest, your money takes 72/6 or 12 years to double.
- To double your money in 10 years, get an interest rate of 72/10 or 7.2%.
- If your country’s GDP grows at 3% a year, the economy doubles in 72/3 or 24 years.
- If your growth slips to 2%, it will double in 36 years. If growth increases to 4%, the economy doubles in 18 years. Given the speed at which technology develops, shaving years off your growth time could be very important.
You can also use the rule of 72 for expenses like inflation or interest:
- If inflation rates go from 2% to 3%, your money will lose half its value in 24 years instead of 36.
- If college tuition increases at 5% per year (which is faster than inflation), tuition costs will double in 72/5 or about 14.4 years. If you pay 15% interest on your credit cards, the amount you owe will double in only 72/15 or 4.8 years!
The rule of 72 shows why a “small” 1% difference in inflation or GDP expansion has a huge effect in forecasting models.
By the way, the Rule of 72 applies to anything that grows, including population. Can you see why a population growth rate of 3% vs 2% could be a huge problem for planning? Instead of needing to double your capacity in 36 years, you only have 24. Twelve years were shaved off your schedule with one percentage point.
Deriving the Formula
Half the fun in using this magic formula is seeing how it’s made. Our goal is to figure out how long it takes for some money (or something else) to double at a certain interest rate.
Let’s start with \$1 since it’s easy to work with (the exact value doesn’t matter). So, suppose we have \$1 and a yearly interest rate R. After one year we have:
1 * (1+R)
For example, at 10% interest, we’d have \$1 * (1 + 0.1) = \$1.10 at the end of the year. After 2 years, we’d have
1 * (1+R) * (1+R)
= 1 * (1+R)^2
And at 10% interest, we have \$1 * (1.1)2 = \$1.21 at the end of year 2. Notice how the dime we earned the first year starts earning money on its own (a penny). Next year we create another dime that starts making pennies for us, along with the small amount the first penny contributes. As Ben Franklin said: “The money that money earns, earns money”, or “The dime the dollar earned, earns a penny.” Cool, huh?
This deceptively small, cumulative growth makes compound interest extremely powerful – Einstein called it one of the most powerful forces in the universe.
Extending this year after year, after N years we have
1 * (1+R)^N
Now, we need to find how long it takes to double — that is, get to 2 dollars. The equation becomes:
1 * (1+R)^N = 2
Basically: How many years at R% interest does it take to get to 2? Not too hard, right? Let’s get to work on this sucka and find N:
1: 1 * (1+R)^N = 2
2: (1+R)^N = 2
3: ln( (1+R)^N ) = ln(2) [natural log of both sides]
4: N * ln(1+R) = .693
5: N * R = .693 [For small R, ln(1+R) ~ R]
6: N = .693 / R
There’s a little trickery on line 5. We use an approximation to say that ln(1+R) = R. It’s pretty close – even at R = .25 the approximation is 10% accurate (check accuracy here). As you use bigger rates, the accuracy will get worse.
Now let’s clean up the formula a bit. We want to use R as an integer (3) rather than a decimal (.03), so we multiply the right hand side by 100:
N = 69.3 / R
There’s one last step: 69.3 is nice and all, but not easily divisible. 72 is closeby, and has many more factors (2, 3, 4, 6, 12…). So the rule of 72 it is. Sorry 69.3, we hardly knew ye. (We could use 70, but again, 72 is nearby and even more divisible; for a mental shortcut, go with the number easiest to divide.)
Extra Credit
Derive a similar rule for tripling your money – just start with
1 * (1+R)^N = 3
Give it a go – if you get stuck, see the rule of 72 for any factor.
Happy math.
A Note On Accuracy
From Colin’s comment on Hacker News, the Rule of 72 works because it’s on the “right side” of 100*ln(2).
100*ln(2) is ~69.3, and 72 rounds up to the bigger side. This is a great choice because the series expansion of r * ln(2) / ln(1 + r/100) is:
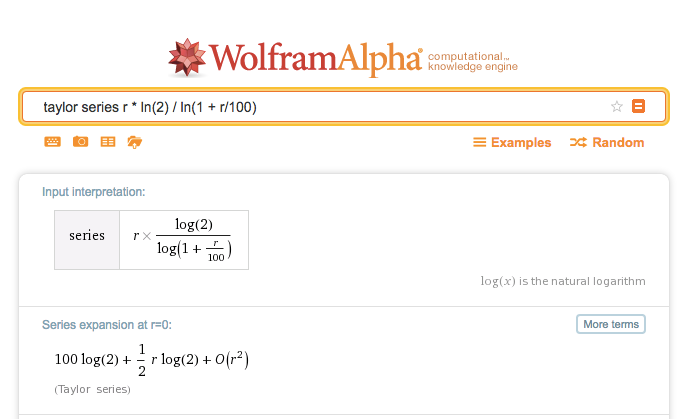
This series expansion is the Calculus Way of showing how far the initial estimate strays from the actual result. The first correction term $\frac{1}{2} r \log(2)$ is small but grows with r. 72 is on the “right side” because it helps us stay in the accurate zone for longer. Neat insight!