In English, we often drop the subject of a phrase:

Who are these signs written for? It's really You, stop or You, yield or You, be alert for bears (I'm not doing it).
After internalizing a language, we can take hints without explicit instructions. But, to put it politely, math isn't usually well-internalized.
Let's get clear about who the "math signs" are referring to.
Imaginary Numbers
Imaginary numbers are often defined as $i^2 = -1$, and written this way they're utterly baffling.
A better restatement is:
![]()
which is still confusing. But what about this:
![]()
It's getting clearer. The instructions are: "Start with 1, multiply by i, multiply by i again, and (somehow) end up at -1".
What could do that? Realizing we start at 1 and end up at -1 helps us visualize something like this:
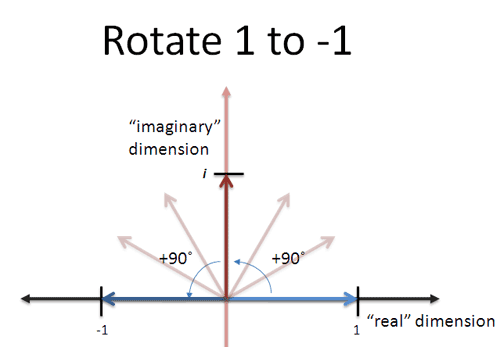
Aha! $i$ is a change (visualized as a rotation) that moves us from positive to negative in two steps (More about imaginary numbers.)
Writing $i^2 = -1$ without a clear subject is confusing. (Don't get me started with $i = \sqrt{-1}$)
Missing the implied subject of "1" in $1* i * i$ caused me years of confusion. I wish this sign was hanging on the classroom wall:

Exponents
Why is $x^0 = 1$ for any value of x? How do we ask for 0 of something and get 1 back out?
Again, let's break it down with a simple example. Here's a typical exponent:
![]()
But it's missing a subject. It's written better as:
![]()
We start at 1 (our default multiplicative scaling factor), scale by x, then scale by x again, ending up at $x^2$. The size of the exponent (2) tells us the number of times to use our "times x" scaling machine.
Stepping back, multiplication is about scaling: 3 is really "1 * 3", or the unit quantity enlarged 3 times.
If we want to scale by x (just once), we write:
![]()
What if we don't plan on using our scaling machine at all?
![]()
The notation is a bit weird, but I'm using empty parenthesis to indicate a lack of action. See, the zero in $x^0$ is that of indifference -- taking no action -- and not obliteration. "Using" $x^0$ means we haven't scaled our original quantity at all.
Subtle, right?
We can take this "growth machine" idea further with the Expand-o-tron 3000.
Imaginary Exponents
Let's combine insights. What does a strange exponent like $e^{i \pi}$ represent?
With our new "implicitly start at 1" perspective, it's really:
![]()
Start at 1 and then apply the growth engine. Here, growth is aimed sideways ($i$) with enough fuel to last for half a circle ($\pi$).
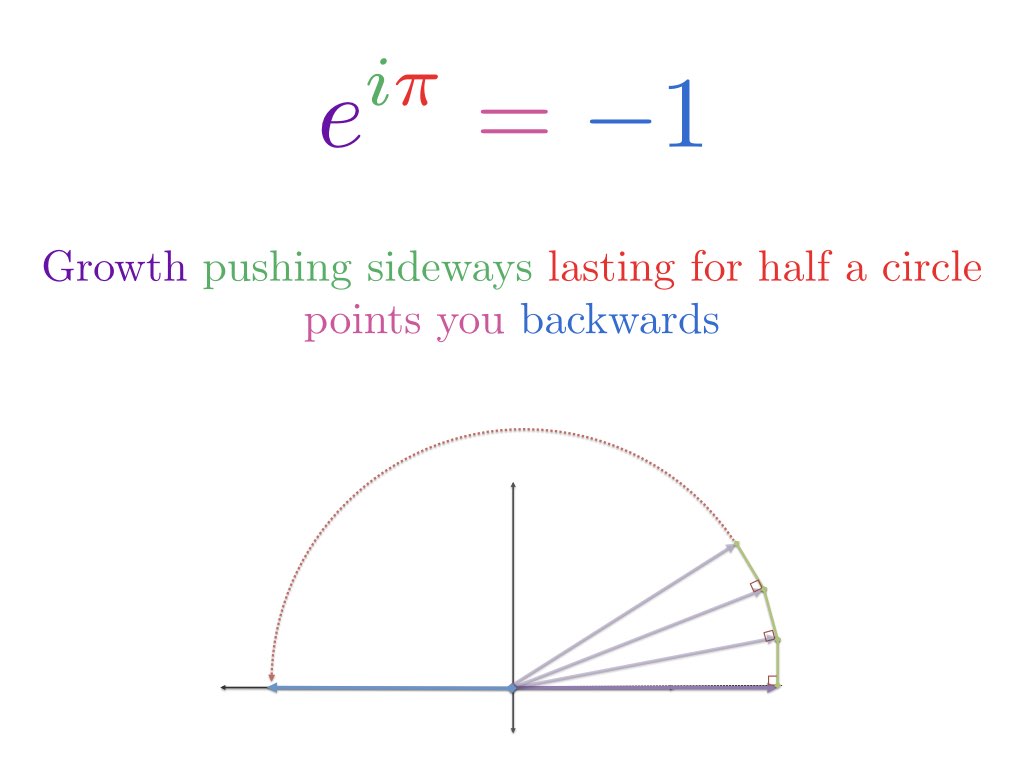
The essence of Euler's Identity is that we are starting at 1 and transforming it with a spin. We aren't creating a negative number out of seemingly positive exponents directly. (See article and video.)
Calculus
Calculus has numerous notational shortcuts. When we write:
![]()
it really means:
![]()
which really means:
![]()
Here's the tricky part. There isn't a single "dx", there's a whole chain of them along the number line. The sentence is something like:
"Hey everyone on the number line! You're all spaced "dx" apart. Take your current position and square it. Then I'll come by and add you all up."
The integral addresses not a single "you" like 1.0, but "them", the countless positions on the number line.
Find the implied subject in an equation, then work to shorten it (Bears!).
Happy math.