To check if you're flexible, you don't need a battery of tests. Just bend down and touch your toes. Was it effortless?
If it's not (and it's not), you know you need to stretch more. The goal isn't the splits, just some self-determined level.
My math goals are similar. I don't need expert proficiency, just a "touch your toes" understanding for the topics I care about.
Example: Exponent Gutcheck
Here's an internal dialog I might have to verify my understand of exponents.
Gutcheck: Roughly speaking, what's $2^{100}$?
It's a large, even, positive number. (This intuition should appear almost instantly. If it takes 10 seconds of thinking to realize it's large, even, or positive, exponents aren't natural.)
Gutcheck: Roughly speaking, what's $2^{-100}$?
It's a tiny, almost undetectable positive decimal. Intuition: It's like going "back in time" by 100 doublings.
Gutcheck: Roughly speaking, what's $2^i$?
Uh oh. Imaginary exponents! With enough intuition, you realize: "It's on the unit circle, at about ln(2) ~ .693 radians."
There's a few gutchecks here. The first is that an imaginary exponent puts you on the unit circle (no matter the base). The next level is a rough "important constant" gutcheck, where you remember ln(2) ~ .693. (Not as important, but good to remember. It helps with things like the Rule of 72)
Gutcheck: Roughly speaking, what's $i^i$?
Oh, here's a tricky one. Remember how we blurted out that $2^{100}$ was large, even, and positive? How proud we were of our quick thinking? Well, what can you say about $i^i$, hotshot?
Yikes. Realizing I couldn't instantly rattle of any properties of $i^i$ meant my intuition for exponents wasn't complete. After getting an intuition for imaginary exponents, the thought becomes:
$i^i$ starts as growth pointing sideways, whose direction is rotated again. It's a positive real number less than 1.0.
Phew. If I truly understand exponents, the gutcheck for $2^{100}$ and $i^i$ should be similar in speed and detail. A painful stretch means I need more understanding.
Additional Examples
The gutcheck process doesn't quite translate to text. These internal back-and-forths happen pre-verbally: I think of a question and quickly feel/visualize/remember an analogy. (It's a gutcheck, not a think-aloud-for-minutes check.)
Here's a few examples I run through from time to time:
Imaginary numbers: What's the cube root of -1?
- Thought: Ok, $i^2 = -1$ means we go from 1 to -1 in two steps. Getting there in 3 steps means a 60-degree rotation (180/3). Oh, we can go the other way too (-60 degrees). Oh, we can flip 180 degrees (180 + 180 + 180 = 360 + 180 = net 180 degree rotation). So there's 3 cube roots of -1.
Fourier Transform: What's the transform of [1 0 0 0]?
- Thought: We want 4 equally strong frequencies (0Hz, 1Hz, 2Hz, 3Hz). They split the strength "1" between them, so we have
[.25 .25 .25 .25](using the notation in the Fourier Transform article).
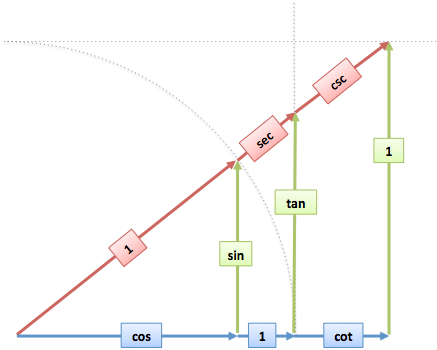
Trigonometry: What's the connection between the 6 major trig functions?
Thought: I think "dome, wall, ceiling" and visualize this trigonometry diagram:
Calculus: Explain the derivative of $x^3$
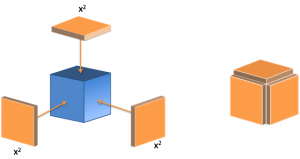
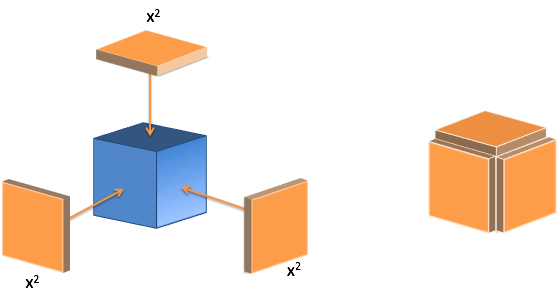
- Thought: $x^3$ is really $x\cdot x \cdot x$. We have 3 perspectives, each seeing a change of $x \cdot x$. The result is $x^2 + x^2 + x^2 = 3x^2$. I also visualize a cube with plates added to it.
Bayes Theorem: What's the plain-English description?
- Thought: chance evidence is real = true positive / (true positives + false positives)
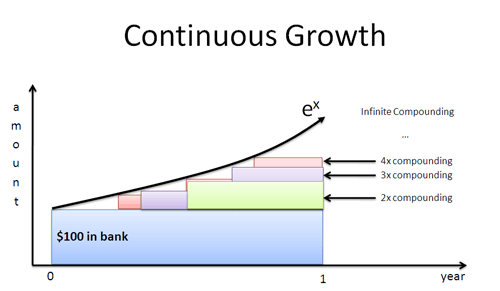
Exponents: What does discrete vs. compound exponential growth look like?
- Thought: I see continuous exponential growth as "filling in the gaps" left by discrete growth.
The key element is speed: an intuitive response should bubble as you hear the question. Struggling for an hour to touch my toes, though admirable, still means I'm not flexible enough.
The goal isn't learning minutia, it's a working understanding of an idea, enough to solve a problem without tremendous effort. It's a diagnostic, not a value judgement. If I struggle, I simply need a better intuition.
Strangely enough, not everyone wants to keep math insights top-of-mind. But pick something that's important to you and occasionally try a 5 second gutcheck on the essentials.
Happy math.