Consequences

• Changing numbers but keeping the average the same. If we keep the total distance to the average the same, the average stays the same (if we reduce the smallest number by some amount, and increase the largest number by the same amount, the average stays the same). You've probably had an intuitive feeling for this in a while: the average of 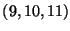= average of 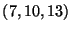. We pull the lowest number down 2 and bring the highest one up 2 to compensate. Also, it shows how you can `redistriubte' a change in distance. Suppose we have 4 points, and the greatest one goes up by 10. How can we maintain the old average? Well, we can reduce a smaller element by 10, or reduce two smaller elements by a total of 10. Again, as long as the total distance stays the same (contribution from all points), we are ok. Example: average of 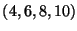= average of 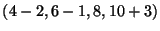. The 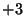cancels the 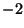and .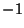
• Center of gravity! Suppose we have numerous 1-pound at different positions along a board, and we want to balance the board. At what point can we balance it? In physics terms, each weight applying a torque to the board, equal to weight * distance. Since the weights are the same (1-pound), the torque is simply equal to distance. We want the location where all the torques, positive and negative, cancel out, so the board does not spin (it balances!). The answer, my friend, is the average! Remember, the average is the point where the sum of distances (torques) above the average = sum of distances (torques) below! So, the board will balance at the center of gravity: hoo-ha! I had always wanted a proof for this (I suspect you have as well), and now you have one. Discussion of different weights to follow :).