Home : Resources : Vector Calculus Relations
Helps to know: Flux Curl Div Grad
Sections: Summary -- Concept Review -- Deriving Theorems

Summary

This is where we tie all of the math together.  Here is my understanding of the following relations and theorems.  We first lay out the definitions, which were explained earlier.

Concept Review

Name
What it means and example
Math Equation
Flux

Amount of something crossing a surface.  Amount of water flowing into a bucket, for example.  Maximum flux when a surface is perpendicular to whatever is flowing.  No flux when surface parallel to flow.  The greater the source, the more flux.
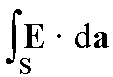Divergence

Flux/volume.  Total amount of flux entering/leaving a surface, divided by volume (flux density).  Pouring water into a bucket creates a divergance, because water is entering and not leaving.  Technically, divergance is a property of a single point.
Circulation


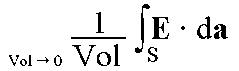Net amount you are pushed along a closed path; whether or not it is possible to get a free ride.  A whirlpool has a net circulation, because you get a "free ride" if you travel in a circle.  In a river you get a free ride downstream, but have to fight your way back upstream (for a closed path).  Result: no "free ride", thus no circulation.

  
Curl Circulation/Area.  Take the amout of circulation around a path, then divide by the area the path encloses. Technically property of a single point (limit as area goes to zero).  


Deriving the Theorems

Now we make what seems like painfully obvious relations given the definitions above.  Remember that it took a lot of smart guys a lot of time to crank out these bad boys. Remeber that these "multiplications" must be performed with integrals (we are usually using ugly shapes).

Intuitive Relation
Fancy Name
Math Equation
Flux = Divergence * Volume Divergence Thm.  
Circulation = Curl * Area Stokes' Theorem  
Flux proportional to source Gauss' Theorem  

Flux/Volume proportional to source/volume
(Divergence) proportional to (source density)

 Gauss' Theorem divided by volume  


Most people aren't interested in the specifics of the math relations and equations, but if you are a student with problem sets (like me) you probably are.  Check out this page for explanations of the math.
Send questions, comments, corrections, and suggestions to [email protected].
Last modified: 8/7/01