Physical Intuition

Ok guys, here we go...

Flux is the amount of something crossing a surface.  This "something" can be water, air, electric field, bananas, or anything you want.  Flux therefore depends on two things:  the surface you are considering (shape, size, orientation) and the source of the flux (magnitude, orientation). This last part is important, because all flux is not equal! You must know the magnitude of what is crossing the surface. Would you rather have a handful of 5 or 20 dollar bills "flux" into your bank account?

The area you are considering is simply the boundary the flux is crossing.   This can be any surface: a spherical shell, a flat plane, or the top of a bucket.   Notice that these boundaries may or may not actually exist, as in the case of the bucket.  The top of the bucket traces out a surface (a circle) but it isn't actually there; we are just considering the flux crossing the region that the circle defines.

Flux is taken at a single instant in time. If the vector field is not changing with time, then this does not matter. If the field does change with time, then you must choose a point in time to examine the flux.

Remember that flux is not "per unit area": it is the total amount that crosses a surface.  Thus, flux may have units of volume (flux is taken at an instant in time). You can certainly speak of the flux at a certain point, but often times you want to know the total flux, not flux/area.

We can easily see that the source helps determine the amount of flux.  If we double the amount of source (i.e. doubling the water flow from a tap) we double the flux through a given surface.

Flux also depends on the orientations of the source and the boundary.  If the boundary is completely facing the source then we get maximum flux.   However, as the boundary tilts away from the source the flux decreases because not as much source is crossing the surface.  Eventually we get zero flux when the source and the boundary are perpendicular. 

This means all of the source is going over the boundary, but none is actually crossing it.  This is like holding a bucket sideways under a waterfall (the source).  No water should go into the bucket (ignoring splashing) because the source and the boundary are perpendicular. Pretty simple stuff so far.

One last point.  With flux we have to designate a positive and negative direction. This decision is arbitrary, but the convention is to have positive flux when things are leaving a closed surface.  For example, lets consider our entire bucket to be a cylindrical surface. If we pour water out of the bucket, we have positive flux (because it is leaving the surface). If we pour water in, we have negative flux.

To sum up, flux is dependent on the size of the surface, magnitude of the source, and the angle between them; all must be specified to find the flux. If we have a fire hose shooting at a small bucket it may have the same flux as a garden hose shooting into a big bucket.  The big bucket can capture more water, but the water is coming in more slowly (less magnitude).  Flux also tells you to hold your bucket facing the source of water in order to fill it up the fastest.  Obvious, yes, but don't you want things (especially math!) to be obvious?

Mathematics

The math for determining the flux through a surface is pretty easy, we can derive it using our intuition. The source of flux in most cases will be a vector field. We will be considering how much of the field is going through our area, taking magnitude into account.

Fundamentally, we must figure out the magnitude of the field passing through each point in our surface, then integrate this over our entire surface.

To find the strength of the field at a point, we must take the dot product of the field direction and the normal to the surface at the point. Why? Again, we want to consider the flux going through the surface. If it is going through at an angle, then only a portion of the magnitude is actually entering the surface. The dot product tells us how much. The equation is:


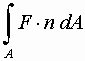
How do we find the normal to a surface? Good question. For surfaces like a plane, the normal is in the same direction for every point (that is, perpendicular to the plane). For a sphere, the normal is in the same direction as r, the position vector. Thus, the top of a sphere has a normal which goes out the top. For shapes more complicated than that, the normal may vary from point to point.

For cases like these, try to break up the shape into subshapes (spheres and planes) and solve the flux through those. Computers exist to calculate more complicated flux problems; I am happy to know how it is done, even if I can't solve it.

Practice problems for the noids: 1 2 3

Examples

Let's look at some examples of flux to fully understand it.  Suppose we have a magical box that allows water to pass right through it.  We put the box under a waterfall, wait a bit, then ask what the flux is.   We want a numerical answer.  What is it?

At first you'd think we'd have to know how much water was falling in the waterfall, the dimensions of the box, etc., but that isn't the case.

Recalling the convention for orientation, the top of the box has a positive direction outward, which is up. The water is falling downwards, into the top of the box.  This means that the top has negative flux.

For the bottom of the box, outward is still defined as positive flux. The water from the waterfall is flowing downwards, out of the bottom.  Thus, the bottom of the box has positive flux.

No Net Flux

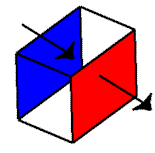Ah... now we see what's happening.  The top of the box says that water is entering, but the bottom says that water is leaving.   We assume the same amount of water enters and leaves (we kept the rate of water falling a constant).  Thus, the net flux is zero. Think of it as  X + (-X) = 0. What if we had increased the rate of water flow with time? Decreased it?

Even though the net flux is zero, it is not necessarily the same situation as zero flux total. If we choose a different surface we may have a positive or negative flux (see examples). Realize the difference between having zero flux because no water is flowing, or having zero flux because it all cancels.

This flux stuff is relatively simple but really helps to understand some of the upcoming theorems. Trying to understand flux by looking at a mess of integrals is not the way to go.

Revelations

You can take the time derivative of flux. If the vector field changes with time, then F is dependent on t, so you can take the time derivative to find the change in flux. However, each flux calculation is taken at a single time; we are simply making calculations at different times.

You can integrate flux, to find out how much has crossed during a certain time. Again, if F is constant with time, then simply multiply the flux at one instant by the duration. If flux changes with time, then you must integrate. Each flux calculation is done at an instant of time, then all are summed.

For my waterfall example, we considered a point in time when the water had been flowing for a while. If we had chosen our point in time early, we could have had negative flux: water had entered the top (remember our orientations?), but there was no water leaving the bottom. Also, when we freeze time, the water entering the top is different than the water leaving the bottom (i.e., not the same molecules of water).

Look at the following example:

There is negative flux as the arrow enters, then positive flux as the arrow exits. But the overall result over a long enough time is no net flux. I didn't mean to be long-winded, but flux is important for understanding many theorems, electricity, and magnetism.