Algebra is really about relationships. How are things connected? Do they move together, or apart, or maybe they’re completely independent?
Normal equations assume an “input to output” connection. That is, we take an input (x=3), plug it into the relationship ($y=x^2$), and observe the result (y=9).
But is that the only way to see a scenario? The setup $y=x^2$ implies that y only moves because of x. But it could be that y just coincidentally equals $x^2$, and some hidden factor is changing them both (the factor changes x to 3 while also changing y to 9).
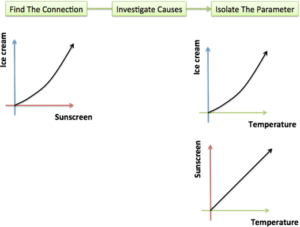
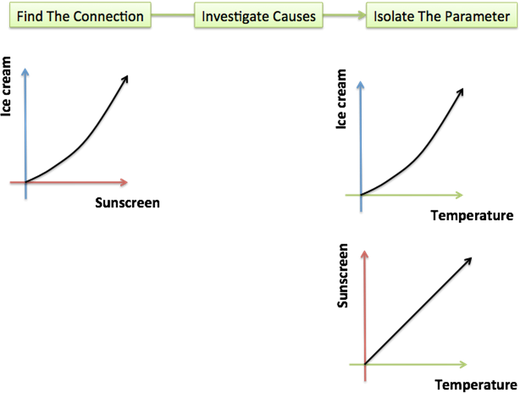
As a real world example: For every degree above 70, our convenience store sells x bottles of sunscreen and $x^2$ pints of ice cream.
We could write the algebra relationship like this:
![]()
And it’s correct… but misleading!
The equation implies sunscreen directly changes the demand for ice cream, when it’s the hidden variable (temperature) that changed them both!
It’s much better to write two separate equations
![]()
![]()
that directly point out the causality. The ideas “temperature impacts ice cream” and “temperature impacts sunscreen” clarify the situation, and we lose information by trying to factor away the common “temperature” portion. Parametric equations get us closer to the real-world relationship.
Don’t Think About Time. Just Look for Root Causes.
A reader pointed out that nearly every parametric equation tutorial uses time as its example parameter. We get so hammered with “parametric equations involve time” that we forget the key insight: parameters point to the cause. Why did we change? (Maybe it was time, or temperature, or perhaps sunscreen really does make you hungry for ice cream.)
Most algebraic equations lay out a connection like $y = x^2$. Parametric equations remind us to look deeper (lost on me until recently; I’d been stuck in the “time/physics” mindset).
Sure, not every setup has a hidden parameter, but isn’t it worth a look?
Update: Eddie Woo made an excellent video using this analogy.
Watch the full series (part 2, part 3), I really loved how he explained the history of the word (para=beside, i.e. you have a hidden variable beside the ones you see). Thanks Eddie!