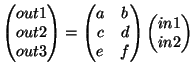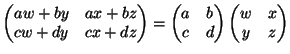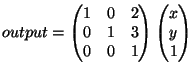


Understanding Linear Algebra
Kalid Azad1
http://www.princeton.edu/~kazad/
Abstract:
This is an intuitive description of linear algebra and its uses. Includes
- Thinking about matrices in terms of inputs/outputs
- What matrices can and cannot do
- How to use matrices to solve transformation problems
I didn't intuitively understand the use of linear algebra and its uses until recently. This tutorial assumes you have had linear algebra before (do a google search for some tutorials), but want a new understanding.
My first problem was only thinking of a matrix as convenient way of writing down a group of numbers. Instead, think of it as a function that takes an input and returns an output:
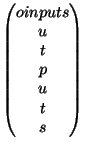 For me, this is a new and useful way of looking at matrices; they are more than just notation. They take their inputs from the right, and return the outputs to the left. Suppose
For me, this is a new and useful way of looking at matrices; they are more than just notation. They take their inputs from the right, and return the outputs to the left. Suppose 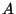 is an array (it doesn't matter what it does). Then we can write
Now, suppose we wanted to take the output of matrix
is an array (it doesn't matter what it does). Then we can write
Now, suppose we wanted to take the output of matrix 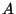 and run it through matrix
and run it through matrix 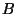 . We can write
So, the input starts down the line from left to right. It is run through
. We can write
So, the input starts down the line from left to right. It is run through 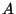 , and the result runs through
, and the result runs through 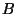 .
When we specify the size of an array, we use the notation R x C (rows by columns) or outputs x inputs. A 3 x 2 array has 3 outputs and 2 inputs:
Why is this useful? Suppose we want to string together some matrices, like we did for
.
When we specify the size of an array, we use the notation R x C (rows by columns) or outputs x inputs. A 3 x 2 array has 3 outputs and 2 inputs:
Why is this useful? Suppose we want to string together some matrices, like we did for 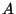 and
and 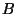 above. What is the relation between their sizes? The answer is simple: the number of outputs of A must equal the inputs of B. If B is expecting 3 items, A had better output 3 items. The inner numbers have to match up when two matrices are multiplied: you can multiply a [M x 3] * [3 x N], but not [M x 3] * [2 x N]. The latter [2 x N] matrix only has 2 outputs, but the [M x 3] matrix is expecting 3 inputs.
This should be clear from the input/output model, but isn't quite as obvious when you look at the mathematical definitions for matrices.
One note about combining matrices: the order matters! Applying matrix
above. What is the relation between their sizes? The answer is simple: the number of outputs of A must equal the inputs of B. If B is expecting 3 items, A had better output 3 items. The inner numbers have to match up when two matrices are multiplied: you can multiply a [M x 3] * [3 x N], but not [M x 3] * [2 x N]. The latter [2 x N] matrix only has 2 outputs, but the [M x 3] matrix is expecting 3 inputs.
This should be clear from the input/output model, but isn't quite as obvious when you look at the mathematical definitions for matrices.
One note about combining matrices: the order matters! Applying matrix 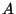 then matrix
then matrix 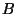 differs from
differs from 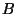 then
then 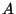 . Sometimes the result may be the same, but it is not necessarily true. Consider the matrices
Flip the order and the result will not be the same.
To specify an element, we use the RC (row-column) notation. So the elements in the first row are (1,1) (1,2) (1,3) etc. In terms of the input/output relationship, output
. Sometimes the result may be the same, but it is not necessarily true. Consider the matrices
Flip the order and the result will not be the same.
To specify an element, we use the RC (row-column) notation. So the elements in the first row are (1,1) (1,2) (1,3) etc. In terms of the input/output relationship, output 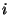 is specified by the ith row. That is, the 1st data point output is entirely determined by the first row. The second element of output is entirely determined by the second row. And so on.
Note that for the identity matrix, we have 1's along the diagonal. This is saying: the first output is simply 1 times the first input (the first element of the input). The second output is 1 times the second input.
The key point: the ith output is determined by the ith row.
As we learned, a matrix takes an input and returns an output. In linear algebra, a matrix performs a linear transformation of the input to the output. This is the key: a matrix transforms its input in a linear way. What does linear really mean? For our purposes, two things.
First, scaling an input should result in a scaled output. That is, if
I was caught in the trap of thinking of a line as linear. It is not, as defined in this sense. Take the equation
is specified by the ith row. That is, the 1st data point output is entirely determined by the first row. The second element of output is entirely determined by the second row. And so on.
Note that for the identity matrix, we have 1's along the diagonal. This is saying: the first output is simply 1 times the first input (the first element of the input). The second output is 1 times the second input.
The key point: the ith output is determined by the ith row.
As we learned, a matrix takes an input and returns an output. In linear algebra, a matrix performs a linear transformation of the input to the output. This is the key: a matrix transforms its input in a linear way. What does linear really mean? For our purposes, two things.
First, scaling an input should result in a scaled output. That is, if
I was caught in the trap of thinking of a line as linear. It is not, as defined in this sense. Take the equation 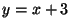 . What is the output when
. What is the output when 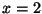 ? If we double x, do we get double the output? No. The constant 3 messes us up. Equations of the form
? If we double x, do we get double the output? No. The constant 3 messes us up. Equations of the form 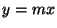 are linear, but NOT
are linear, but NOT
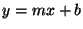 . To set it straight: the equations are for a line, but they are not linear.
Second, a combination of inputs leads to the sum of their outputs. This means if
The fancy word for this is linear superposition, and is used often in physics. The main ideas is that the sum of the inputs leads to the sum of the outputs. For the line example, take
. To set it straight: the equations are for a line, but they are not linear.
Second, a combination of inputs leads to the sum of their outputs. This means if
The fancy word for this is linear superposition, and is used often in physics. The main ideas is that the sum of the inputs leads to the sum of the outputs. For the line example, take 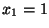 and
and 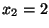 . Does
. Does
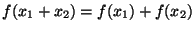 ? Again, no.
Why do matrices follow this? If you recall, matrices are just linear combinations of their inputs: they can multiply the inputs by constants, and add them together. There is no addition of constants to mess up the linearity.
So, what do matrices do? They perform linear transformations, such as
? Again, no.
Why do matrices follow this? If you recall, matrices are just linear combinations of their inputs: they can multiply the inputs by constants, and add them together. There is no addition of constants to mess up the linearity.
So, what do matrices do? They perform linear transformations, such as
- Scaling. If you have a range of 0-10 and want to make it 0-5, a matrix can help you (or you can just divide by 2).
- Rotation. You must rotate about the origin. For tricks around this, see the end of this section.
What don't they do?
- Translation. You can't slide things around. If you have a range 0-10 and want to make it 10-20, multiplying by a matrix won't help (all you want to do is add 10). Similarly, you can't change a range 0-10 into 3-5 because 0 has to go to 3, which requires a translation.
However, there are two ways around this. The easy way is to add a "`constant"' matrix to make equations for lines, such as
The other way is to use a matrix of one-higher dimension. Keep reading if using higher dimesions doesn't make your eyes glaze over (otherwise, adding a constant will work fine).
Take your pencil and lay it on the desk. Keep one end fixed, and spin the other end around. This is like a 2-d vector, stuck in the second dimension. You could theoretically stretch out your pencil (scaling) or rotate it around the fixed end2. Now let's do a cool transformation: lift one end of the pencil (keeping the fixed end on the desk), and stand it stright up. This is the (0 0 1) vector, i.e., a vector only in the z direction. This is also the origin (0 0) when we project the vector back into the 2-d plane (to project a vector, just take the first 2 components; it is the where the tip of the pencil would be if you "`dropped it straight down"' to the paper level). Tilt this vector (er, pencil) slightly forward, keeping the base at the same location. Now look at the projection again.
First, notice that this operation is a rotation in the 3-d plane. We kept the end of the pencil fixed, and just tilted it slightly, a rotation in 3-space. But what happened in the 2-d plane? The projection of the origin moved slightly forward! That is, the location of the origin in the 2-d plane moved - this is a translation. The origin was originally represented by (0 0 1), the straight-up pencil. After the rotation, the new origin had an x and y component - the origin had moved after the matrix operation.
So, by using a matrix of one higher dimesion, we can translate smaller-dimensional vectors, and rotate about any point (which is simply a translation to the new point then a rotation). Cool, eh? That example took me a while to think of, you'd better have enjoyed it! It's a cool concept that a rotation in a higher dimension leads to a translation in this dimension.
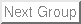
For kicks, let's write out the math. Let's say you want to move the 2-d origin to (2,3) instead of (0,0). First, consider every 2-d vector as a 3-d vector: the point (1, 2) becomes (1, 2, x). What should x be? First of all, it should NOT be 0. If it was, then adding some constant * x would do no good. So, x has to be nonzero, and a simple choice is to make 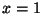 .
Next, we look at the 3-d matrix. We want to keep the x and y components the same (no stretching/rotation), just add 2 to the x component, and 3 to the y. We could do this by
If you do the math, you see that this adds 2 to the x component, and 3 to the y component, and leaves the z component the same. It is the same as adding the vector (2 3 0) to (x y 1).
Key point: translation can be done by rotating in a higher dimension.
Need to update this eventually.
Understanding Linear Algebra
.
Next, we look at the 3-d matrix. We want to keep the x and y components the same (no stretching/rotation), just add 2 to the x component, and 3 to the y. We could do this by
If you do the math, you see that this adds 2 to the x component, and 3 to the y component, and leaves the z component the same. It is the same as adding the vector (2 3 0) to (x y 1).
Key point: translation can be done by rotating in a higher dimension.
Need to update this eventually.
Understanding Linear Algebra
This document was generated using the
LaTeX2HTML translator Version 2002 (1.62)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -image_type gif -local_icons -split 0 linearalgebra.tex
The translation was initiated by Kalid M. Azad on 2002-12-07
Footnotes
- ... Azad1
- Copyright 2002. May be reproduced for educational purposes.
- ... end2
- A vector is just 2 numbers, which specify one end of the pencil. The other end is fixed, and assumed to be the origin (0,0). You cannot rotate it about the center, for example, because then the center becomes the new origin.



Kalid M. Azad
2002-12-07
 For me, this is a new and useful way of looking at matrices; they are more than just notation. They take their inputs from the right, and return the outputs to the left. Suppose
For me, this is a new and useful way of looking at matrices; they are more than just notation. They take their inputs from the right, and return the outputs to the left. Suppose