I hate to break it to you, but all graphs are not created equal. I realized this just the other day, wrote an article, and had my computer crash. The article vanished, but I'm determined to get this idea on the web. It's a simple but interesting concept.
To begin, let's look at the types of graphs. Just as the universe can be divided into "bananas" and "non-bananas", I'm going to make a similar division: "map-graphs" and "non-map graphs".
Map graphs are graphs where the x and y axes correspond to distance. Thus, a coordinate represents a location of some sort. Non-map graphs, or all other graphs, are simply graphs where the coordinates do not imply distance, but instead production, population, time, or some other variable. We shall see that these types of graphs are not the same.
Consider this typical example of a map graph:
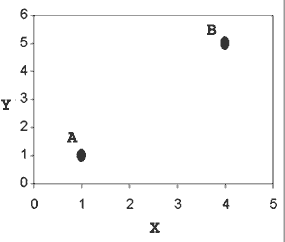
Suppose we want to get from the proverbial point A (1, 1)to point B (4, 5). Suppose that there is some cost associated with the trip: hours of time, gallons of gas, or whatever unit of expense you want. The point is that we need to minimize this expense.
We know that the shortest distance between two points is a straight line. Using Pythagoreas' theorem, we know that the distance is 5 units (making a 3-4-5 right triangle). If we instead went from A to (4,1), then from (4,1) to B, it would be a distance of 7 units. Obviously, going from A to B directly is the least expensive path.
Now consider this typical "non-map" graph:
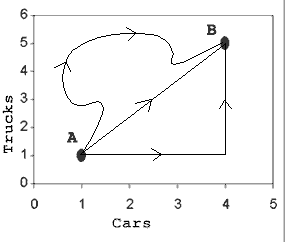
Suppose a car rental company wants to increase its inventory. Currently it is at point A, with one car and one truck. It wants to get to point B (4 cars, 5 trucks). The cost of the trip is simply the cost of buying the new cars and trucks. How should it buy its vehicles?
This isn't a very hard problem. We can see that no matter what "path" they take to B, the cost is the same -- they end up buying 3 cars and 4 trucks. They can buy all their cars then all their trucks, vice-versa, or anything in between.
Why are these two examples different? The simple reason is that distance does not matter in non-map graphs. Quite simply, if a map doesn't have distance on its axes, then distance in the graph does not matter at all. Pythagoreas' theorem does not help us. Knowing that the shortest distance between two points is a line does not help us. We can't escape the fact that we must end up with 4 cars and 5 trucks. But is this the end of the story?
No, it's not the end of the story
So, it appears that in map graphs, we want the direct route. In non-map graphs, we are stuck and can't take a shortcut. Consider this map graph:
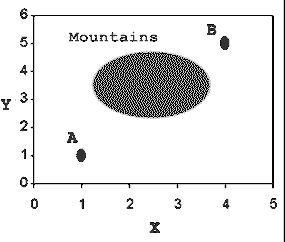
We still want to get from A to B, but now we must cross the mountains. Suppose that in the mountains, the cost is 10 times normal. Suddenly the direct route doesn't make as much sense. Taking the long route around the sides (From A to (4,1) to B) is cheaper.
On distance graphs where the cost varies from point to point, the cheapest path may no longer be a straight line. It will vary on the cost at each point, which may be determined by a function, for instance. More on this later :)
On map graphs, distance usually matters. A straight line is the shortest path, but not necessarily the "cheapest". Be careful.
On other maps, thedistance of a path in the graph doesn't matter in --
it isn't measured on the axes!
Last modified: 8/7/01