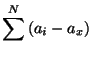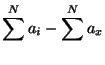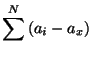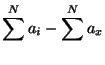Next: Interpretation
Up: Mathematical Properties of the
Previous: Introduction and definition
Contents
First, consider how far each number is from the average. Suppose we have three numbers 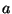 ,
, 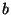 and
and 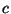 , with an average of
, with an average of
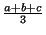 .
How far is each number from the average? Well, each number (
.
How far is each number from the average? Well, each number (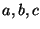 ) is simply a point on the number line and the distance to the average is a simple subtraction. So, the distance from
) is simply a point on the number line and the distance to the average is a simple subtraction. So, the distance from 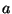 to the average is
to the average is
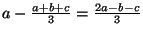 Likewise, the distance of
Likewise, the distance of 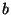 and
and 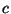 to the average is
to the average is
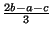 and
and
 , respectively. These numbers, by themselves, aren't that useful.
However, let's ask a more important question: what is the total distance of
, respectively. These numbers, by themselves, aren't that useful.
However, let's ask a more important question: what is the total distance of 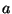 ,
, 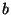 and
and 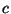 to the average? The answer:
to the average? The answer:
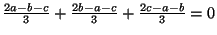 Now this is interesting. The sum of the distances to the average (from each point) is zero. Note that we are not talking about the absolute value of distance (such as `point a is 3 units away from the average'). We are using positive and negative distances (our convetion was
Now this is interesting. The sum of the distances to the average (from each point) is zero. Note that we are not talking about the absolute value of distance (such as `point a is 3 units away from the average'). We are using positive and negative distances (our convetion was
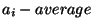 ). A positive distance means a point is greater than the average, and a negative distance indacates the point is less than the average.
This example was just for 3 numbers. Of course, it works in general as well. Take n numbers (
). A positive distance means a point is greater than the average, and a negative distance indacates the point is less than the average.
This example was just for 3 numbers. Of course, it works in general as well. Take n numbers (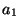 to
to 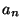 ) and call the average
) and call the average 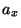 (
(
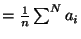 ). The sum of the distances to the average is
). The sum of the distances to the average is
Not a hard proof, eh?




Next: Interpretation
Up: Mathematical Properties of the
Previous: Introduction and definition
Contents
Kalid M. Azad
2002-10-31