- ... center-of-gravity).1
- Copyright 2002. May be reproduced non-commercial purposes.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... explanation.2
- I had hoped the intuitive argument had worked, but I guess not. Let
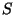 be the subset of numbers smaller than the average, and
be the subset of numbers smaller than the average, and 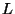 be the subset larger. Let
be the subset larger. Let 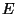 be the subset of all numbers equal to the average.
be the subset of all numbers equal to the average. 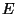 ,
, 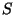 and
and 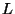 are mutually exclusive (a number cannot be both greater, less than, or equal to the average).
Call the average
are mutually exclusive (a number cannot be both greater, less than, or equal to the average).
Call the average 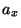 , and let
, and let 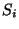 be an element in
be an element in 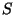 (similarly for
(similarly for 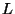 and
and 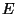 ). The facts are
). The facts are
-
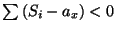 , true because each
, true because each 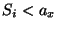 by definition
by definition
-
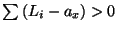 , true for similar reasons
, true for similar reasons
-
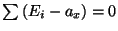 , true because each
, true because each 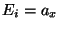 by definition
by definition
-
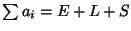 , since the sets are mutually exclusive and each number
, since the sets are mutually exclusive and each number 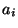 must fall into exactly one category
must fall into exactly one category
-
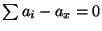 , shown earlier
, shown earlier
Therefore,
which is the result we sought to prove. Phew! Sorry for the roundabout proof, but you asked for it!
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
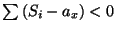 , true because each
, true because each 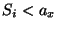 by definition
by definition
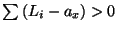 , true for similar reasons
, true for similar reasons
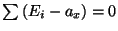 , true because each
, true because each 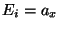 by definition
by definition
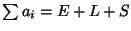 , since the sets are mutually exclusive and each number
, since the sets are mutually exclusive and each number 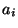 must fall into exactly one category
must fall into exactly one category
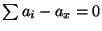 , shown earlier
, shown earlier