Intro
Derivatives are rates of change, which can be seen and calculated explicitly with vectors. Integrals are simply a summation and have the same units as the funcion being intergrated. These facts can help you set up and evaluate integrals and derivatives.
The Vector Derivative
The derivative is a rate of change. It measures how much a function changes when you "wiggle" one of the variables. That's easy enough, but it gets interesting (a.k.a. difficult) when you start taking derivatives of vector functions. Things can get confusing.
The method I use for vectors is pretty simple. If you know that a vector is changing, draw the vector before the change, then the vector afterwards. Now, draw a vector from the head of the first vector to the head of the second vector. This new vector is the derivative. In the diagram below, the position vector goes changes. The position vector is simply the vector drawn from the origin to a point. The point changed from R1 to R2.
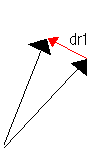 |
Remember that vectors only have magnitude and direction. You can slide them around and won't change anything about them. So, when taking derivatives, remember that the position doesn't necessarily matter. The position vector is an interesting case: it is simply the position of something relative to the origin, so there is a location associated with the tail of the vector (the origin). But strictly speaking, vectors can still slide around (i.e. you could slide your entire coordinate system around and not change anything). |
The position vector is an interesting case: it
is simply the position of something relative to the origin, so there is
a location associated with the tail of the vector (the origin).
But strictly speaking, vectors can still slide around (i.e. you could
slide your entire coordinate system around and not change anything).
Now, if you want to take the second derivative, you
repeat the process. You plot out a bunch of R's, then draw in the
dr's. Then you draw in the dr's of the dr's... or the second derivative.
If we went around in a circle and wanted to find the second derivative:
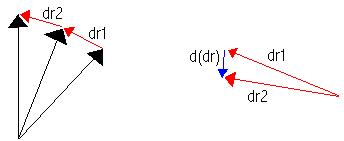 |
The blue arrow represents the second derivative, or the derivative of the derivative- hence the d(dr).Notice that I slid dr2 to have its tail meet up with the tail of dr1 (but I didn't change its orientation). Then I drew in the derivative as before. It's ok to slide vectors because they are independent of position. |
For you physics buffs, this is an example of centripetal
acceleration. If you swing a bucket in a circle, you must keep pulling
it towards you to keep it going. The blue arrow is the acceleration
(second derivative of position), which shows this. The red arrows
represent its velocity at any point. If you were to let go of the
bucket, it would travel in the direction of the red arrow. To be
formal, we were taking the time derivative of R because we were watching
how it changed in time.
Derivative: Tiny Changes
The derivative can also be viewed as a tiny, infintely small change. Because the vectors in the previous example were changing with time, we took time derivatives. Position is measured in meters. Take the time derivative, and you get meters/second (velocity). Take it again, and you get meters/(second^2), or acceleration. Every time you take a derivative, you are changing the units.
When you take derivatives of functions of position by chopping it up into little peices, you are not changing the units. You simply have a tiny peice of length instead of the whole legth. But you still have units of meters, for example. This leads me to my next point...
Integrals: Adding up Tiny Changes
When you integrate a function, you don't change its units. An integral is simply a sum, so you still have the same units as whatever it is you are summing. For example, when you take
![]()
You are multiplying velocity by a dt (a little element of time). The integral sums up all those little peices, but you will still have units of (velocity * time) or distance. Addition doesn't change units, and that's what an integral essentially is.
This is useful because it serves as a good check as
to whether you integrated a function properly. In pure mathematics,
when dealing only with variables, you can't check your units. In
physics you can make sure the integral you get makes sense. Let's
look at an example, which a TA in physics showed us. Suppose, for
fun, you want to integrate (x,L in meters):
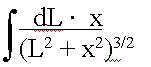
This is tough integral, it had our physics class stumped for a while. Let's look at the units. We have units of (meters*meters) on the top. Remember that dL has the same units as L; it is simply a tiny peice of L, and still has the same units. On the bottom, we have (L^2 + x^2), which has units of (meter^2). But we are taking this to the 3/2 power, so we get units of (meters^3) on the bottom. The net result is (meters^2) / (meters^3), or (1/meter).
The stuff inside the integral has units of (1/meter), so whatever function we get for the integral must have units of (1/meter) as well. Ok, from here it gets a little crazy but if you want to see the process of how my physics TA tore up this integral here. The final function is:
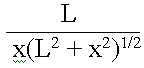
Let's check units on this bad boy. We have (meters) on the top. On the bottom, we have meters squared. When we divide, we see that we get units of (1/meter), the same units as the function inside the integral. This little trick can help you find the integral as well as check to make sure you have the right one. The steps of the derivation are also available.
The point is that your antiderivative
should have the same units as the function you are integrating, because
an integral is only a sum. Adding numbers doesn't change their units
(i.e. 3 meters + 2 meters = 5 meters). Later.
Last modified: 8/7/01