Summary

Complex numbers can be represented in cartesian form (a + bi) or in polar form (r*e^(i * theta) ).  The magnitude of a complex number is found by multiplying by its complex conjugate (a-bi) and then taking the square root of the product.  In polar form, r is the magnitude.

Imaginary Numbers: What are they?

Easy answer:  The square root of -1 is represented by the number "i".  "i" looks like a variable but it is not; it is the number such that its sqaure equals negative one.  The square roots of other negative numbers can be represented in terms of i.  For example, the square root of -9 is 3i.

Tricky stuff:  How a negative number can even have a square boggles the mind.  That's why "i" is imaginary, I suppose, but the fact that we defined and use it is funky.  Another point:   don't all numbers have two square roots?  The square root of 9 is 3 and -3.  What about -1?  It should have two roots as well (since we said that it is allowed to have roots).  Maybe -i will work as well (just like -3 works for 9).  Well, if we square -i we get

(-i) * (-i)  = (-1)i * (-1)i  = i * i = -1.

Another point: imaginary numbers have real squares. Why? When you square a number b*i   (like 3i, or -6i), you get:

(bi)*(bi) =(b * b)(i * i) = -(b^2).  

So no matter what number b you choose, you get a real result.  Fourth powers are another matter, but sticking to squares we are safe.

Whoa.  So +i and -i have the same square.   Why do we choose one over the other?  I shall return to this shortly, but for now I will let the excitement build.

Complex Numbers

We now have two types of numbers: real, which are all the regular numbers you know and love, and imaginary numbers, the numbers that are square roots of negative numbers.  It is easy to tell them apart: imaginary numbers have an "i".  Real numbers don't.  Now, complex numbers are numbers which have two parts: a real part and an imaginary part.  One way to write them is like this:  a + bi.   "a" is the real part (no i) and "bi" is the imaginary part (has an i).  An example of some complex numbers are:
3 + 4i      a=3,  b=4
3            a=3,  b=0
-6i          a=0,  b=-6

As you can see, every number can be written as a complex number.  Some numbers, like 5 or -9 don't have imaginary parts, and other numbers, like 3i, don't have real parts. Complex numbers are commonly written in the form

z = a +bi    (z is complex, a and b are real).

Notice that z is a single number.  It has two components, but it is still one number.  Think of it in terms of fractions: a fraction is a single number that has two parts: a numerator and a denominator. In general, each component of the fraction is different from the fraction itself.   The same goes for complex numbers: z has two components (1 real and 1 imaginary), and each component alone is (generally) different from z. The components combine to create the complex number z.

Graphing Complex Numbers

Using a + bi notation, we can even draw complex numbers on the complex plane. We are used to x and y axis: we plotted points as (x,y) pairs.  Now, instead of having x and y coordinates, we have real and imaginary coordinates.  Notice how the complex numbers can be broken down into (a,b) pairs.  3+4i becomes (3,4) on the complex plane. 

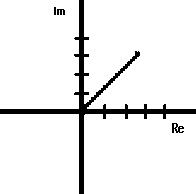
We draw a vector from the origin (0,0) to the point (a, b) that represents the complex number.  3 +3i  looks like this, with imaginary numbers on the vertical and real numbers on the horizontal:

This is just like a normal graph, except we have changed the labels on the axes...

You probably know that a point can be represented in cartesian or polar coordiantes. Cartesian coordiantes are in the form (x,y) and give the two (or more) components of a point. Polar coordinates use a direction and magnitude, and have points in the form (r, theta). 

For example, the point (1,1) in cartesian is (2^.5, 45) in polar.  45 represents the direction (45 degrees above the horizontal) and 2^.5 represents the amount of distance to go (thank you Pythagoras).  The angles start at zero and go counter-clockwise. To go 1 unit downward: 

cartesian: (0,-1) 
polar:  (1, 270).

To convert between the two:
Cartesian:  ( a, b)           
Polar:  r = sqrt(a^2  +  b^2)  [Pythagoran thm], theta = arctan(b/a)

Polar: ( r, theta )
Cartesian: a  = r*cos(theta) b = r*sin(theta)

You don't have to memorize these by any means. Draw a triangle and you can figure it out (link). It's better to learn the intuition behind a concept and derive it when you need it. Intuition is hard to forget; formulas are easy.

[An aside: To express a point in two dimensions you need two peices of data. We are used to the data coming in an (x,y) pair.  Now we see it can also be represented as an (r, theta) pair.  Are there any more ways to represent a point on a plane? To represent a point in three dimensions, we need three pieces of data. There are a few ways to do this (link).]

You will probably seen theta written in terms of radians. Polar coordinates may seem like a hassle: we have to take our complex number and figure out the magnitude and direction. With cartesian coordinates, it is simply (a, b). The next section will justify why we use polar.

Incredible Math Relation

Ok, I'll admit that very few things in math can be called "exciting".  Intersting, maybe (don't roll your eyes) but exciting?  This, my friends, is one of those rare moments.  I was in hysterics when I first learned of it.  The relation is:

This formula is just... amazing.  It relates e, which is an irrational (infinite decimal places) and funky number to begin with, to i, an imaginary numbers, and also to sine and cosine, which are just regular functions that have rational values .  Whoa.  To see why it is true, click here.  For example, e^(i*pi) = -1.  That equation has two irrantional numbers, and somehow the exponential e pops out a negative number.  Ok, that's enough blathering about the beauty of that equation, let's see what it can do.

Suppose we multiply both sides by some number r.  Then we get:



Let's look at this for a bit.  It is strikingly similar to some of the equations for converting between cartesian and polar coordinates.  Indeed,  (rcos(theta), rsin(theta)) is the (x,y) pair for a point originally expressed in (r, theta) form.   But the sin has an i term, so the number is complex.  Now we have an (a,b) term, with a = rcos(theta) and b = rsin(theta).

We have found the polar form for complex numbers.  Instead of being an (r, theta) pair we can write any complex number z as:

z = a +bi  or   z = re^(i*theta)

The rules for converting between the two are the same.  r = sqrt(a^2 + b^2) and theta = arctan(b/a)
If we choose the right numbers for r and theta, then z = a +bi = re^(i * theta).   This is all thanks to the beauty of the above formula.

Complex Conjugates and Magnitudes

Remember how you were at the edge of your seat wondering why we choose +i instead of -i as the square root of -1?  Now we can see where it comes in.

The normal method of finding a magnitude is to square a number and then take its square root.  For positive real numbers this just gives us the original number, and for negative real numbers (like -9) it will give the absolute value (its magnitude).   Thus, both 9 and -9 have the same magnitude of 9.  They are the same distance from the origin, just in different directions.

Complex numbers aren't quite so simple.  Taking 1 + i as an example, if we try and square this and take the square root we get:  magnitude(?) =  sqrt((1+i)^2)   = sqrt(1 +2i -1) = sqrt(2i).  But we showed earlier that imaginary numbers can't have square roots. (LINK WHY).  Uh oh.

Complex conjugates save the day.  Because our decision to define i as positive was arbitrary, we can't exclude the possibility of a negative i.  We define the complex conjugate of (a + bi) as (a - bi).  If z is a complex number, its complex conjugate is usually written as z with a bar over it.  Now, instead of squaring a complex number then taking its square root, we multiply it by its complex conjugate then take the square root.  For any number (a + bi) we get

Magnitude = sqrt( (a+bi) * (a -bi) ) = sqrt(a^2   +abi  -abi  + b^2)  = sqrt(a^2  +  b^2).

It looks just like the formula for regular cartesian coordinates!  (Pythagorean theorem to find lengths).  Thus, the magnitude of (3 + 4i) is sqrt(9 + 16) = 5.  On a last note, if you want to find the complex conjugate of any complex number, just switch all the i's to "-i".  It doesn't matter if they are in exponentials or denominators or inside square roots:  just switch them all.  For complex numbers in polar form (re^(i*theta)), the magnitude is just r.

The polar form of imaginary numbers is useful because multiplication becomes addition when you are dealing with exponentials.  This is much, much easier than expanding out loads of cosine and sine terms.  Also, you don't have to remember the sine and cosine angle addition formulas; the exponentitals can do it for you.  This is very useful when you are analyzing circuits.