| Number Sense |
|---|
| Mental Math Shortcuts |
| Building a Sense of Scale |
| Visual Arithmetic |
| Prime Numbers |
| Changing Bases |
| Understanding Averages |
| Real-world Logarithms |
| High School Essentials |
|---|
| Imaginary Numbers |
| Degrees vs. Radians |
| The number e |
| The natural logarithm |
| Exponents |
| Interest Rates |
| Discovering Pi |
| Combinations / Permutations |
| Similarity |
| Calculus |
|---|
| Gentle introduction |
| Derivatives I |
| Derivatives II |
| Integrals as multiplication |
| Limits |
| University Essentials |
|---|
| Sine Waves |
| Euler's Formula |
| Fourier Transform |
| Probability & Statistics Intro |
| Vector Calculus |
|---|
| Dot Product |
| Gradient |
| Divergence |
| Flux |
| Curl |
| Circulation |
| Learning |
|---|
| Developing Math Intuition |
| Why Do We Study Math? |
| Using Analogies |
| Simplicity vs. Complexity |
| Business |
|---|
| Rule of 72 |
| Pareto Principle (80/20 Rule) |
| Stock Market Basics |
| Accounting Basics |
| Thoughts |
|---|
| Happiness |
| Know thyself |
| On blogging |
Lesson 1: Calculus In A Few Minutes
Welcome to the BetterExplained calculus course! A few reminders before we start:
-
You'll get 2 emails/week for 4-5 weeks (Tues & Thurs). They should take 15-20 mins max (the more learning in less time, the better). If it's taking longer, let me know.
-
Feedback is welcome. There's no homework, but I'd love to know what's working. If you're on a computer, you can probably complete the survey from inside your email. Otherwise (if on a phone or tablet), click the link.
Ok! Let's see how much calculus insight we can build over a few hours of "class time". As mentioned in the course overview, we'll start with high-level analogies and refine our understanding.
Calculus In 1 Minute: Use X-Ray and Time-Lapse Vision
We usually take shapes, formulas, and situations at face value. Calculus gives us a few viewpoints to dig deeper:
-
X-Ray Vision: You see the hidden structure buried inside a result. You don't just see the tree, you know it's made of rings, with another growing as we speak.
 (source)
(source) -
Time-Lapse Vision: You see an object and see its future path laid out (cool superpower, eh?). "Hey, there's the moon. For the next few days it'll be white, but on the sixth it'll be low in the sky, in a color I like. I'll take a photo then.".
 (source)
(source)
So why is Calculus useful? Instead of static scenarios, we can dig one level deeper. Imagine being able to turn on X-Ray or Time-Lapse vision at will. That object over there, how was it put together? What's its future?
Calculus In 10 Minutes: See Patterns Step-By-Step
What do X-Ray and Time-Lapse vision have in common? They examine patterns step-by-step, layer-by-layer.
For example, here's a few similar-looking formulas:
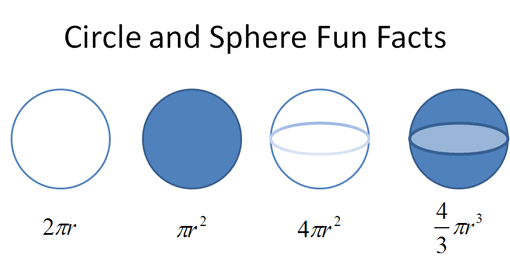
We have a vague feeling they're connected, right? Let's see where this leads.
Suppose we know the equation for circumference (2 * pi * r) and want to figure out the equation for area. What can we do?
This is a tough question. Squares are easy to measure, but what can we do with an ever-curving shape?
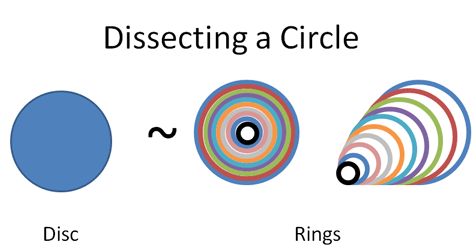
Calculus to the rescue. Let's use our X-Ray vision to realize a disc is really just a bunch of rings put together. Similar to a tree trunk, here's a "step-by-step" view of a filled-in circle:
Why does this viewpoint help? Well, let's unroll those curled-up rings so they're easier to measure:
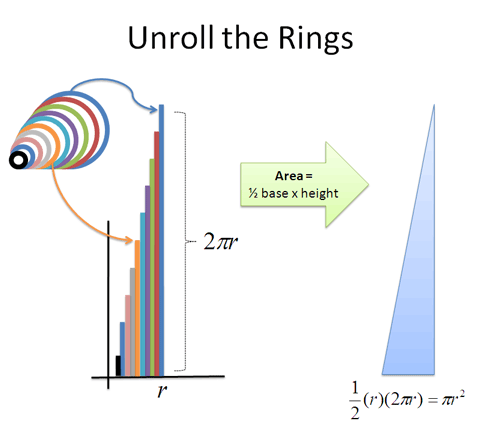
Whoa! We have a bunch of straightened rings, which form a triangle (Wikipedia has an animation also).
The height of the largest ring is the full circumference (2 * pi * r), and each ring gets smaller. The height of each ring depends on its original distance from the center; the ring 3 inches from the center has a height of 2 * pi * 3 inches. The smallest ring is a pinpoint, more or less, without any height at all.
And because triangles are easier to measure than circles, finding the area isn't too much trouble. The area of the “ring triangle” = 1/2 base * height = 1/2 * r * (2 * pi * r) = pi * r^2, which is the formula for a circle's area!
Our X-Ray vision revealed a vastly simpler approach to measuring a curvy shape. We realized a circle and a set of glued-together rings were really the same. From another perspective, a filled-in disc is the "time lapse" of a ring that got larger and larger.
So… What Can I Do With Calculus?
It depends. What can you do with arithmetic?
If you expect to find premade problems with division signs floating in midair, you'll be disappointed. Meanwhile, you'll pass a chef chopping potatoes, a psychologist asking for your mood (1 to 10), and someone loaning a friend a few dollars for dinner (by the way: negative numbers were considered absurd into the 1750s). Arithmetic provides metaphors that transcend computation; once seen, they are difficult to leave behind.
Calculus can offer similar insights: it's a step-by-step view of the world. Do we need X-Ray and Time Lapse vision all the time? Nope. But they're nice perspectives to "turn on" when we face a puzzling situation. What steps got us here? What's the next thing that will happen? Where does our future path lead?
See, Official Calculus™ starts you off by manipulating equations with exacting mathematical standards. Rigorous, perhaps, but not motivating or memorable. We can bang together a few trashcan lids, enjoy the rump-shaking rhythm, and then look forward to exploring deeper.
So don't worry about computations, just play around: what elements in your everyday life, if you wanted to, could you see with a step-by-step viewpoint?
We'll sharpen this up with more specific examples next time.